В одному дослiдi вiдносно iншого

Розглянемо два дослiди а i b, вiдповiдно з результатами А1, A2,..., Аi,..., Ami результатами В1, B2,..., Вj,..., Bni вiдомими iмовiрностями цих результатів Р(А1), Р(А2),..., Р(Ai) i Р(В1), Р(В2),..., Р(Bj). Вiзьмемо далi складний дослiд аb, який полягає в тому, що водночас здiйснюються дослiди а i b. Спробуємо обчислити середню власну iнформацiю, що мiститься в якому-небуть результатi складного дослiду (Ai, Bj) або, iншими словами, ентропiю дослiду ab. По визначенню ентропiя складного дослiду рiвна

H(a,b) = -SР(Ai,Bj) log P(Ai,Вj). (1. 26)

ij

З iншого боку, ентропiя першого дослiду a рiвна

H(a,b) = -SР(Ai) log P(Ai) (1. 27)

i

Пiдставимо далi в (1. 27) Р(Ai), що входять в перший спiвмножник кожного доданку в виглядi

P(Ai) = -SP(Ai,Вj) (1. 28).

j

Вiдзначимо, що вираз (1. 28) являє собою запис формули повної iмовiрностi для подiї Ai, тобто формулу (1. 12). Пiсля подстановки (1.28) в (1. 27) отримаємо

H(a) = -SSР(Ai,Bj) log P(Ai) (1.29)

i j

Аналогiчно ентропiя дослiду b може бути представлена в виглядi

H(b) = -SSР(Ai,Bj) log P(Вj) (1.30)

i j

Якщо a i b - незалежнi дослiди, то для кожної пари результатiв Aii Bj

P (Ai,Bj) = P(Ai) P(Bj),

отже,

log Р(Аi,Вj)=log Р(Ai) + log Р(Bj). (1.31)

Пiдставляючи далi (1. 31) в (1. 26), отримаємо

H(a,b)= - SSР(Ai,Bj) log P(Ai) - SSР(Ai,Bj) log P(Вj)

i j i j

Або, маючи на увазi (1. 29) i (1. 30),

H (ab) =H (а) + H (b). (1. 32)

Таким чином, при незалежних дослiдах ентропiя складного дослiду рiвна сумi ентропiй кожного дослiду.

В бiльш загальному випадку, коли дослiди залежнi, iмовiрнiсть пари результатів Ai, Bjможе бути представлена в виглядi

Р (Аi, Вj) =Р(Аi) Р(Вj). (1. 33)

Вiдповiдно

log Р (Аi,Вj) = log Р(Ai) + logPAi(Bj). (1. 33')

Тут PAi(Bj) означає умовну iмовiрнiсть результата Вj, якщо вiдомо, що дослiд а закiнчився результатом Ai. Підставляючи (1. 33') в (1. 20), отримаємо

H(a,b) = -SSР(Ai,Bj) log P(Ai) - SSР(Ai,Bj) log PAi(Вj) (1.34)

i j i j

Перша сума в виразi (1.34) являє собою (1.29) або ентропiю дослiду а. Другу суму в (1.34) називають умовною ентропiєю дослiду b, припускаючи, що який-небуть результат дослiду а мав мiсце. Цю ентропiю дослiду b за умови дослiду а позначимо Ha(b). Тодi ентропiя складного дослiду, тобто (1. 34), може бути записана

H (а, b)=H (a) + Ha(b). (1. 35)

По визначенню умовна ентропiя являє собою вираз

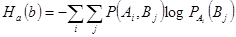(1.36)

або, маючи на увазi (1. 33),

(1.37)

i j

Внутрiшня сума в виразi (1. 37), очевидно, являє собою ентропiю дослiду b за умови, що дослiд a закiнчився конкретним результатом Ai. Справдi ця внутрiшня сума нiчим не вiдрiзняється вiд виразу (1.19), за винятком того, що замiсть iмовiрностей Р(Bj) тут стоять iмовiрностi результатiв Bjпри умовi, що був конкретний результат Ai. Цю умовну ентропiю дослiду b при конкретному результатi дослiду а позначимо через HAi(b)

НАi(b) = - SРAi(Bj) log PAi(Вj) (1.38)

j

При цьому вираз (1. 37), тобто умовна ентропiя дослiду b при дослiдi a, може бути представлено як усереднення виразу (1. 38) по всiм результатам дослiду а, тобто по всiм Аi

Нa(b) = - SР(Aj)HAi(Вj) (1.39)

i

Таким чином, умовна ентропiя дослiду b при дослiдi а являє собою середню власну iнформацiю, що полягає в результатi дослiду b в середньому при будь-якому результатi дослiду а.

Розглянемо властивостi умовної ентропiї.

1. Якщо дослiди a i b незалежнi, те умовна ентропiя рiвна безумовнiй

Ha(b) = H (b). (1.40)

Властивiсть (1.40) безпосередньо слiдує з порiвняння формул (1.32) i (1.35), виведених вiдповiдно для випадкiв незалежних i залежних дослiдiв.

2. Якщо результати першого дослiду, скажемо дослiду а, повнiстю визначають результати iншого дослiду b (тобто дослiд а визначає дослiд b), то умовна ентропiя рiвна нулю

Ha(b) = 0. (1.41)

Дiйсно, бо при цьому всi РAi(Bj) рiвнi або одиницi або нулю, в вiдповiдностi з (1.38) величина HAi(b) рiвна нулю для всiх результатiв Аiдослiду а. НAi(b)=0, тому вираз (1. 39) перетворюється в нуль.

3. Умовна ентропiя завжди менша або рiвна безумовної ентропiї, тобто

Ha(b) £ H (b). (1.42)

Знак рiвностi має мiсце при незалежностi дослiду а i b (див. властивiсть 1).

Для доказу спiввiдношення (1. 42) утворимо рiзницю

Ha(b) - H (b) = -SSР(Ai,Bj) log PAi(Вj) -(- SSР(Ai,Bj) log P(Вj)) = (1.43)

i j i j

= - SSР(Ai,Bj) log (P(Вj)/PAi(Вj))

i j

Застосуємо до виразу (1.43) властивiсть логарифмiчної функцiї (1. 23), поклавши тут w = Р(Bj)/PAi(Bj). Тодi

Ha(b) - H (b) £ log e SSР(Ai,Bj)(P(Вj)/PAi(Вj) - 1)=0

i j

Дiйсно, права частина цiєї нерiвностi легко може бути записана як

log e [SР(Ai)SР(Bj) - 1] =0

i j

що тотожно рiвна нулю. Отже, Ha(b) - H (b) £ 0, тобто доведена нерiвнiсть (1.42). Знак рiвностi має мiсце при w=0, тобто при P(Bj)/PAi(Bj) =1 для будь-яких Аii Bj, або тодi, коли дослiди а i b незалежнi.

Ми отримали результат, що умовна ентропiя дослiду b, якщо проведений дослiд а, завжди менша або рiвна ентропiї дослiду b. Однак умовна ентропiя дослiду b при конкретному результатi дослiду а, HAi(b) може бути i меншою i бiльшою ентропiї дослiду b, Н(b). Цей факт можна пояснити слiдуючим чином. Для одних результатiв Аiмає мiсце HAi(b) < H(b), для iнших, навпаки, HAi(b) буде бiльше H(b). Але в середньому в сенсi формули (1. 39) ентропiя Hа(b) буде завжди менша або рiвна ентропiї H (b).

Пояснимо сказане прикладом.

Нехай хворий страждає яким-небуть одним з трьох захворювань B1, B2, B3. При цьому iмовiрнiсть того, що вiн страждає першим захворюванням, рiвна Р(B1)=0.98, а iмовiрностi iнших захворювань вiдповiдно рiвнi Р(B2) =P(B3) =0,01. Подальше дослiдження хворого a може мати два результата А1i A2, причому результат А1виключає захворювання B1, а результат A2повнiстю пiдтверджує наявнiсть захворювання B1i, отже, виключає захворювання B2i В3. Обчислимо ентропiю (невизначенiсть) ситуацiї до проведення дослiдження a. Тодi

H(b)= - [P(B1) log P(B1) + P(B2) log P(B2) + P(B3) log P(B3)] =

= - [0,98 log0,98 + 0,01 log 0,01 + 0,01 log 0,01] = 0,16 бiт.

Вiдзначимо, що Р(A2) =0, 98, а Р(A1) = 0, 02, бо поява цих результатов еквiвалентна подiям B1i notВ1. Крiм того, очевидно, що PA1(B1) = 0, PA1(B2)=PA1(B3) = 1/2, бо результат А1виключає захворювання B1i при цьому залишаються два рiвноiмовiрних захворювання: В2i B3. З iншого боку, PA2(B1)=1 i PA2(B2) = PA2(B3) = 0. Обчислимо тепер ентропiю (невизначенiсть) ситуацiї при конкретних результатах дослiдження a

НА1(b)= - [PA1(B1) log PA1(B1)+РА1(B2) log PA1(B2)+РA1(B3) log PA1(B3)] =

= 0 + 1/2log2 + 1/2log2= 1 бiт,

НА2(b)= - [PA2(B1) log PA2(B1)+PA2(B2) log PA2(B2)+PA2(B3) log PA2(B3)] =

=0 + 0 + 0 = 0.

Таким чином, ми бачимо, що результат А1збiльшує ентропiю (невизначенiсть) ситуацiї, а результат А2зменшує. Цей факт має просте фiзичне обгрунтування. Справдi, до проведення дослiдження a, розподiл iмовiрностей захворювань був таким, що ми могли бути майже впевненi в тому, що хворий страждає захворюванням В1, i в цьому сенсi невизначенiсть ситуацiї була надто невелика (0, 16 бiт).

Однак, якщо в результатi дослiдження a з'являється результат A1(що в загалi-то малоймовiрно, але можливо), то в цьому випадку виявиться, що хворий може мати яке-небуть одне з двох рiвноможливих захворювань B2або B3. В цьому випадку невизначенiсть ситуацiї виявиться вже значно бiльшою (1 бiт). Але якщо в результатi дослiду a виникне результат А2(що вiдбувається в переважнiй бiльшостi випадкiв, в середньому в 98 випадках з 100), та це твердо вкаже на наявнiсть у хворого захворювання В1, i, отже жодної невизначенностi бiльше не буде (HA2(b)=0). Середня ж ентропiя ситуацiї b за умови проведення iспиту а буде все-таки менша, нiж Н(b)

Ha(b) = Р(А1)НA1(b)+Р(А2)НA2(b)=0, 02·1+0, 98·0=0, 02 бiт,

тобто

Ha(b) < H(b).

4. Оскiльки всяка ентропiя додатня, то вираз (1. 38) iстотно додатнiй, а отже, додатня i (1. 39). Отже,

Ha(b) ³ 0. (1.44)

Об'єднуючи (1. 42) i (1. 44), отримаємо

0 £ Ha(b) £ H (b). (1.45)

5. В якостi п'ятої властивостi умовної ентропiї виведемо тотожнiсть

Н(а) + Ha(b) = H (b) + Hb(a). (1.46)

Вираз (1.46) безпосередньо слiдує з того факту, що складний дослiд

ab нiчим нe вiдрiзняється вiд дослiду ba. Отже,

H(аb) = H(ba)

або

H(a) + Ha(b) = H(b) + Hb(a).

Розглянемо тепер питання про середню iнформацiю, що мiститься в одному дослiдi вiдносно iншого, або, iнакше кажучи, про середню вiдносну iнформацiю. Нехай невизначенiсть, зв'язана з деяким дослiдом b, виражається ентропiєю H(b). Здiйснення деякого iншого дослiду а зменшує невизначенiсть дослiду b. Це виражається в тому, що умовна ентропiя ситуацiї b пiсля проведення дослiду a стає меншою, нiж ентропiя ситуацiї b, тобто

Ha(b) £ H(b).

Різниця H(b) - Ha(b) являє собою зменшення невизначеностi дослiду b або, iншими словами, зменшення середньої власної iнформацiї в дослiдi b. Це зменшення власної iнформацiї в дослiдi b прeдcтавляє собою ту кiлькiсть iнформацiї, що несе дослiд a вiдносно дослiду b. В вiдповiдностi з цим середньою iнформацiєю одного дослiду вiдносно iншого називають вираз

I(ab) = H(b) - Ha(b). (1.47)

Враховуючи вираз (1.46), можемо записати

H(b) - Ha(b) = H(a) - Hb(a) (1. 48)

або

I(ab) = I(ba) (1. 49)

Таким чином, середня iнформацiя, що полягає в одному дослiдi вiдносно iншого, рiвна середнiй iнформацiї, укладеній в iншому дослiдi вiдносно першого. Оскiльки умовна ентропiя - величина iстотно додатня, то з (1. 47) i (1. 48) слiдує, що

I(ab) £ H (a), I (ab) £ H (b). (1. 50)

Нерівність (1. 50) виражае той факт, що середня iнформацiя, що мiститься в одному дослiдi вiдносно iншого, менша, нiж iнформацiя, укладена в середньому в кожному результатi цього дослiду вiдносно самого себе.

Вiдноcна iнформацiя, що мiститься в конкретному результатi дослiду a, тобто в Аi, вiдносно всiх результатів дослiду b (в середньому) в вiдповiдностi з визначенням (1. 47), рiвна

I (Aib) = H (b) - HAi(b). (1.51)

Вона може бути i додатньою i вiдємною, оскiльки НАi(b) може бути i менше, i бiльше Н(b). В протилежнiсть цьому iнформацiя I(ab) завжди додатня, оскiльки На(b) завжди менше або рiвне H(b). Якщо же нас цiкавить iнформацiя, що мiститься в конкретному результаті дослiду ab (тобто в Ai) вiдносно конкретного результату дослiду b (тобто Bj), то в вирзi (1.51) слiд опустити усереднення по результатам Bj. Тодi отримаємо

I(Аi, Вj) = - log Р(Bj) - (- log PAi(Bj)) = log (PAi(Bj)/P(Bj)),

тобто вираз (1. 17).

Дата добавления: 2015-07-21