До цих пiр ми розглядали надлишковiсть як небажане явище, що приводиться до надмiрного збiльшення коду. В цьому роздiлi ми покажемо, що в багатьох випадках корисно спецiально вводити надлишковiсть з метою збiльшення помiхостiйкостi системи, передбачаючи можливiсть вiдкриття i виправлення помилок при передачi iнформацiї.
Найбiльш простим засобом виявлення на приймальному кiнцi можливої помилки в повiдомленнях, що передаються є так звана, перевiрка на парнiсть. Припустимо, ми передаємо iнформацiю за допомогою двйкового коду i припустимо, що група з n символiв може мiстити не бiльш однiєї помилки. Для здiйснення перевiрки на кiнцi, що передає, розбиваємо кожне повiдомлення на групи з m=n-1 символiв. До кожної групи дописуємо один символ так, щоб сума цифр в отриманiй групi з n символiв була парною. Наприклад, при n=6
сигнал Провiрочний сигнал що
символ передається
10110 1 101101
10111 0 101110
Це дозволяє на приймальному кiнцi вiдразу виявити одноразову помилку, якщо прийнятий сигнал виявиться непарним. Для цього прийняте повiдомлення дiлять на групи з n символiв i визначають парнiсть суми цифр кожної групи. Пiсля перевiрки останнiй символ в кожнiй групi вiдкидається.
Однак такий простий засiб не дозволяє з'ясувати, в якому саме мiсцi нашого коду вiдбулася помилка. Крiм того, такий пiдхiд не дозволяє виявити подвiйну помилку, бо помилковий сигнал залишиться парним.
В 1950 г. Р. Хеммiнг поклав початок дуже важливим роботам по створенню кодiв, що виявляють i виправляють помилки, запропонований ним пiдхiд полягає в додаваннi не одного, а декiлькох провiрочних символiв i здiйсненнi декiлькох перевiрок на парнiсть в вiдповiдностi з виробленими правилами.
Розглянемо основну iдею цього методу. Маємо сукупнiсть з n двiйкових символiв i припускаємо, що в кодах довжиною n не зустрiчається бiльше однiєї помилки. З n символiв кодового слова m символiв будемо використовувати для передачi сигналу (повiдомлення), а iншi k символiв - для перевiрки
n=m+ k. (1. 94)
За допомогою k провiрочних символiв можна скласти 2kрiзноманiтних комбiнацiй (рiзноманiтних двiйкових чисел), кожна з котрих повинна вказувати на один з наступних фактiв:
1) помилки немає; 2) помилка в першому символi; 3) помилка в другому символi i т. д.; n+1)помилка в символi номер n. Всього одержується n+1 вказiвка. Звiдки слiдує умова
2k³n+1. (1.95)
Умова (1.95) дозволяє вибрати найменше число провiрочних символiв, необхiдних для виявлення i виправлення одиничної помилки в кодi довжиною n символiв. Таким чином, k - найменше цiле число, що задовольнить (1. 95). Сказане iлюструє таблиця, в якій найбiльше число символiв n може бути перевiрене застосуванням вiд 1 до 5 проверочнiх символiв k.
| Кількість перевірочних символів k | Всього символів n | Інформаційні символи m =n-k |
Спочатку розглянемо метод Хеммінга на прикладi третього випадку таблицi, так званого коду '4 з 7', де чотири двiйкових символа видiленi для iнформацiї, а три - для перевiрки. Таким чином, наша мета полягає в виявленнi i локалiзацiї помилок в припущеннi, що в групi з семи двiйкових символiв нiколи не зустрiчається бiльше однiєї помилки. Для цього складемо наступнi провiрочнi суми, в вiдповiдностi з якими на кiнцi, що передає будемо заповнювати вмiст провiрочни розрядiв, а на приймальному кiнцi перевiряти цi суми на парнiсть.
Нехай y1, y2, y3, y4 - вмiст m iнформацiйних розрядiв нашого сигналу (в даному випадку m=4). Крiм того, с5, c6, c7 - вмiст k проверочнiх розрядiв (в даному випадку k=3). Тодi провiрочнi суми мають вигляд:
Сума I: y1+ y2+ y3+ c5,
Сума II: y1+ y2+ y4+ c6, (1. 96)
Сума III: y1+ y3+ y4+ c7,
В залежностi вiд конкретного змiсту символiв y1, y2, y3, y4 встановлюється змiст символiв c5, c6, c7, так, щоб суми (1. 90) були парними. На табл. 1 крестики вiдповiдають методу складання перевiрочнiх сум.На приймальному кiнцi знов складаються всi суми (1.96). Якщо вони парнi, то помилки немає. Якщо виявилася непарною одна з сум, то помилка в провiрочному символi цiєї суми, бо всi iншi
Таблиця 1
| Інформація | Перевірка | |||||||||||||
| y1 | y2 | y3 | y4 | c5 | c6 | C7 | ||||||||
| X | X | X | X | Сума І | ||||||||||
| X | X | X | X | Сума ІІ | ||||||||||
| X | X | X | X | Сума ІІІ | ||||||||||
символи входять i в iншi суми, а вони парнi. Якщо двi суми непарнi, то помилка в тому символi, що входить в обидвi цi суми, але нс входить в третю. Нарештi, якщо всi суми непарнi, то помилка в тому символi, що входить в всi цi суми. Як тiльки визначено, в якому символi помилка, її виправлення не представляє складностi. Потрiбно замiсть даного символу поставити протилежний (якщо стоїть 0, поставити 1, а якщо 1, поставити 0). Проiлюструємо сказане прикладом використання коду “4 з 7”.
Маємо повiдомлення, кодоване двiйковими символами.
0000100010100100.
Подiлимо його на групи по чотири символи в кожнiй
0000 1000 1010 0100.
На кiнцi, кожної з чотиризначних груп доповнимо ще трьома символами (c5, c6, c7), вiдповiдними перевiркам на парнiсть згiдно (1.96).
Тодi отримаємо
0000000 1000111 1010010 0100110.
В пiдсумку повiдомлення, що передається буде мати вигляд 0000000100011110100100100110.
На приймальному кiнцi повiдомлення розбивається на групи по сiм знакiв, здiйснюється перевiрка на парнiсть в вiдповiдностi з сумами (1.96), якщо необхiдно виправляються помилки, а пiсля цього в кожнiй семизначнiй групi усуваються три останнi знаки. Таким чином ми вiдновимо вхiдне повiдомлення. Приклад коду '4 з 7' пояснює загальний метод, запропонований Хеммiнгом. Вiн полягає в наступному. Складаємо стiльки перевiрочних сум, скiльки перевiрочних символiв встановлює нерiвнiсть (1.95). Кожна перевiрочна сума мiстить тiльки один перевiрочний символ ci, i кожний даний провiрочний символ зустрiчається в усiх сумах тiльки один раз. Перший символ y1(з m iнформацiйних) входить у всi суми, кожний з наступних y2...yk+1символiв входить в k-1 з k проверочнiх сум. Пiсля цього, якщо m>k iншi yk+2... символiв входять в (k - 2) провірочних сум. Так, можна розмiстити ще 1/2 k (k-1)
Таблиця 2.
| y1 | Y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | y11 | c12 | c13 | c14 | c15 |
| X | X | X | X | - | X | X | X | - | - | - | X | - | - | - |
| X | X | X | - | X | X | - | - | X | X | - | - | X | - | - |
| X | X | - | X | X | - | X | - | X | - | X | - | - | X | - |
| X | - | X | X | X | - | - | X | - | X | X | - | - | - | X |
символiв з залишившихся m iнформацiйних i т. д. Цей метод утворення провірочних сум наочно iлюструє приклад коду '11 з 15' (табл. 2).
Викладене поширюється i на бiльш складнi випадки, коли код може водночас мiстити двi помилки, три i т. д. При цьому умова (1.95), кiлькiсть необхiдних провірочних символiв, змiнюється. Наприклад, якщо припустити, що код може мiстити двi помилки, то до n+1 вказiвки (помилок немає, в такому-то мiсцi є одинична помилка) повиннi додатися 
вказiвок можливих комбiнацiй по двi помилки, тобто повинно мати мiсце
. (1.97)
Якщо в кодi можливi i три помилки, то повиннi додатися ще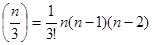 
вказiвок можливих комбiнацiй по три помилки, тобто
2k>= (n+1) + l/2n(n -1) + 1/3! n(n - 1), (1.98)
i т. д.
Таким чином, ми бачимо, що кiлькiсть провiрочнiх символiв дуже швидко росте. Тому на практицi вигiднiше розбивати все повiдомлення на пiдгрупи так, щоб в кожнiй підгруппi було по можливостi не бiльше однiєї помилки, нiж мати дiло з довгим повiдомленням, припускаючи можливiсть кратної помилки.
Викладенi iдеї можна дуже наочно проiлюструвати геометрично. Уявимо собi, що для передачi можливих N повiдомлень ми користуємось n-розрядним двiйковим кодом. Кожне n-розрядне двiйкове слово можна уявити точкою в n-мiрному просторi, координати якого - значення символiв по кожному розряду (0 або 1). Якщо n=3, то ми маємо звичайний тривимiрний простiр, де означенi точки утворять вершини одиничного куба (рис. 7).
 |
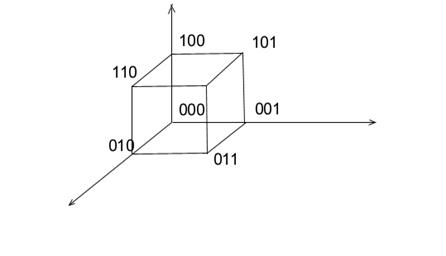Домовимося називати вiдстанню dij мiж двома кодовiми словами (двома вершинами куба) найменше число їхнiх ребер, що роздiляють їх або, що те ж саме, кiлькiсть порозряднiх не-збiгiв в цих двох словах. Наприклад, вiдстань мiж двiйковими словами 101100 i 100110 рiвна dij=2. Якщо код не володiє надлишковiстю, тобто N=2n, те кожному кодовому слову вiдповiдає своє повiдомлення i мiнiмальний iнтервал при такому кодуваннi dijmin рiвний 1. Природньо, що такий код не може виявити помилку, бо будь-яка помилка перекладає дане слово в iнше, вiдповiдне iншому повiдомленню. Цю помилку не можна буде вiдрiзнити вiд iншого сигналу. Якщо ж N<2n, тобто має мiсце надлишковiсть, те не всi вершини куба можна взяти в якостi кодових слiв, вiдповiдних повiдомленням, а тiльки частину з них. Тодi можна вибрати код, при якому dijmin=2, i виявити одну помилку (але не виправити). Дiйсно, наявнiсть помилки призведе до того, що помилкове слово буде стояти вiд iншого кодового слова на iнтервалi, рiвному dij=1. А це для iстинних повiдомлень неможливо. Але подвiйну помилку вже виявити не можна, бо вона переведе наше слово в iнше кодовое слово, вiдповiдне iншому iстинному повiдомленню. Якщо вибрати код з мiнiмальним iнтервалом dij min=3, то одинична помилка призведе до отримання слова, що стоїть на вiдстанi dij=1 вiд вхiдного. Але вiд iнших слiв коду, вiдповiдних iстинним повiдомленням, воно буде вiдстояти мiнiмум на двi одиницi. Це дозволяє знайти викривлене слово (вхiдне), тобто виправити помилку. Таким чином, код з dijmin=3 дозволяє виправити одиничну помилку i виявити подвiйну. В загальному випадку, якщо N << 2n(бiльша надлишковiсть), то при мiнiмальнiй вiдстанi мiж словами, рiвнiй dijmin = 2(m+1) (m - цiле, додатнє), можна побудувати код, що виправляє v-кратну помилку (v= 1, 2,..., m) або що виявляє 2v-кратну.
Дата добавления: 2015-07-21; просмотров: 108 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Експоненціальний закон збiльшення числа повiдомленнь | | | Огляд найбільш вживаних |