Надлишковість

Маємо деяку систему дослiдів a1, a2,..., am. Власна середня кiлькiсть iнформацiї на один результат кожного окремого дослiду рiвна його ентропiї

I(a1) = Н(a1),

I(a2) = Н(a2),

.............

I(am) = Н(am),

Власна середня кiлькiсть iнформацiї на один результат складного дослiду, являючого собою сукупнiсть дослiдiв a1,..., am, рiвна ентропiї складного дослiду I(a1,..., am) = H(a1,..., am).

Якщо дослiди a1,..., amнезалежнi, то в вiдповiдностi з (1. 32)

H (а1,..., am) = H(a1) + H(a2) +... + H(am)

або

I (a1,..., am) = SI(ai) (1.52)

i

Однак, якщо дослiди a1,..., amзалежнi, то в вiдповiдностi з (1. 32), (1. 35) i (1.42)

H(а1,..., am) £ H(a1) + H(a2) +... + H(am)

або

I (а1,..., am) £ I(a1) + I(a2) +... + I(am) (1.53)

З (1. 52) i (1.53) слiдує, що з системи незалежних дослiдiв(випробувань) можна отримати бiльше iнформацiї, нiж з системи залежних. I навпаки, для отримання тiєї же iнформацiї в випадку незалежностi можна обiйтися меншою кiлькiстю випробувань. Це важливо мати на увазi при розробцi бiльш ощадливої системи iспитiв. Отже, в випадку залежних дослiдiв для отримання тiєї ж кiлькостi iнформацiї, ми повиннi проводити бiльшу кiлькiсть iспитiв, нiж це мiнiмально необхiдно, тобто вводити деяку надлишковiсть в iспитах. Для кiлькiсної оцiнки цiєї надлишковостi вводиться коєфiцiент надлишковостi, що виражає собою вiдносне зменшення кiлькостi одержуваної iнформацiї внаслiдок залежностi мiж дослiдом

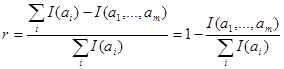(1. 54)

Поняття надлишковостi можна розповсюдити i на процес кодування i вiдповiдно прийти до подання надлишковостi коду. Припустимо, що для передачi деякої системи повiдомлень ми використаємо кодовi слова довжиною в n символiв, маючи в своєму розпорядженнi код з L рiзноманiтними символами (L - алфавiт коду). Якщо поява того або iншого символу на даному фiксованому мiсцi (в даному розрядi) кодового слова рiвноможлива, то кiлькiсть iнформацiї, що полягає в появi деякого символу на цьому фiксованому мiсцi, рiвна

I (ai) = log L. [див (1.21)].

В той же час, якщо символи в кодовому словi незалежнi, тобто iмовiрнiсть появи даного символу не залежить вiд того, якi символи мiстяться в iнших розрядах кодового слова, то кiлькiсть iнформацiї, що мiститься в системi символiв (тобто в кодовому словi в цiлому), рiвна

n

S I(ai) = n log L (1. 55)

i=1

Вираз (1. 55) являє собою максимальну власну кiлькiсть iнформацiї, що може мiститися в кодовому словi довжиною в n символiв при алфавiтi L. Однак, якщо код мiстить обмеження, що полягає, наприклад, в неможливостi деяких комбiнацiй символiв (детермiнiстськi обмеження) або в тому, що iмовiрнiсть появи якого-небуть символа залежить вiд того, якi символи є в iнших розрядах кодового слова (ймовiрнiснi обмеження), то кiлькiсть iнформацiї, що мiститься в середньому в кожному кодовому словi, буде менша (1. 55). Цю кiлькiсть iнформацiї позначимо I(a1,..., an). Такий код буде володiти надлишковістю, рiвною в вiдповiдностi з (1.54).

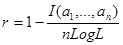(1. 56)

Тут сенс надлишковостi полягає в тому, що для передачi тiєї ж кiлькостi iнформацiї ми змушенi користуватися бiльш довгими кодовими словами, нiж це необхiдно.

Наведемо приклад. Розглянемо двiйково-десятковий код, що часто використовується для подання кiлькiсних величi.

0-0000

1-0001

2-0010

3-0011

4-0100

5-0101

6-0110

7-0111

8-1000

9-1001

В цьому кодi кожний розряд десяткового числа представляється 4 двiйковими розрядами. В даному кодi можливi 10 рiзноманiтних повiдомлень, i якщо всi вони рiвноiмовiрнi (оптимальний випадок в сенсi максимума iнформацiї), то кiлькiсть iнформацiї на повiдомлення буде рiвно

I(a1,..., a4) = log 10.

А коефiцiент надлишковостi в вiдповiдностi з (1. 50) рiвний

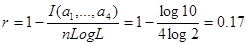
оскiльки тут n=4 i L=2. Отримана в цьому прикладi надлишковiсть двiйково-десяткового коду з'являється внаслiдок того, що ряд комбiнацiй в цьому кодi недопустимі. А саме, тут не мають сенсу наступнi комбiнацiї: 1010, 1011, 1100, 1101, 1111. До цих пiр ми розглядали надлишковість як небажане явище, що приводить або до необхiдностi ставити бiльше число дослiдiв, нiж це мiнiмально необхiдно, або в випадку кодування повiдомлень користуватися кодами бiльшої довжини. Однак надлишковість має позитивну сторону, так як дозволяє одержувати бiльшу надiйнiсть результатiв (дублювання дослiду), або, в випадку кодування, спецiальний ввiд надлишковостi дозволяє виявляти й виправляти помилки, що виникають в процесi передачi коду по каналу зв'язку.

Дата добавления: 2015-07-21