Мiра iнформацiї

Кожне повiдомлення, кожна iнформацiя про той або iнший фактi має немов би двi сторони: конкретний змiст даного повiдомлення, даного факту, i статистичнi (ймовiрноснi) властивостi, що дозволяють порiвнювати цiлком разнорiднi повiдомлення по тій різноманітності станiв, з якими цi повiдомлення зв'язанi.

Наприклад, повiдомлення про те, що в технiчнiй системi управлiння вийшов з ладу один з двох однаково надiйних (або, краще сказати, ненадiйних) підсилювачів, i повiдомлення, що Н. народила хлопчика, зв'язанi з однiєю i тіею же різноманітністю - з появою одного з двох рівноможливих фактiв.

В сенсi зв'язаної з цими фактами різноманітності цi два повiдомлення цiлком однаковi, хоча їхнiй конкретний змiст iстотно різниться. Відмічена нами спiльнiсть має далеко iдучі наслiдки, а саме: як ми побачимо нижче, ефективнi системи зв'язку для передачi повідомлень одного типу будуть настiльки ж хороші i для передачi вiдомостей другого типу. Ця спiльнiсть i дозволяє ввести деякi загальнi поняття, зв'язанi з рiзноманiтними повiдомленнями, незважючи на їхню різнорідність. Таким поняттям, що висловлює мiру різноманітності ситуацiї, зв'язаної з тим або iншим повiдомленням або фактом, є iнформацiя.

Вiдзначимо, що поняття кiлькостi iнформацiї, укладеної в тому або iншому повiдомленнi, зв'язане з iмовiрнiстю цього повiдомлення, тобто з деякою статистичною сукупнiстю. Введемо бiльш точне визначення iнформацiї як деякої кiлькiсної величини - деякої мiри.

По визначенню кiлькiсть власної iнформацiї, укладеної в повiдомленнi Аiрiвна логарифму його iмовiрностi, взятому зі зворотнім знаком

I (Аі) = -log(P(Ai)). (1.14)

Знак мiнус в формулi (1.14) введений для того, щоб зробити цей вираз iстотно позитивним [0£Р(Аi)£1, Þ логарифм Р (Ai) - величина вiдємна]. Виразу (1. 14) можна придати вигляд

I(Аi) = log 1/P(Ai) (1.15)

з якого слiдує, що чим менша iмовiрнiсть появи повiдомлення Ai, тим бiльшою кiлькiстю iнформацiї воно володiє.

Сенс вводу логарифмичної мiри в виразах (1.14) i (1.15) полягає в наданнi кiлькостi iнформацiї властивостi адитивності. Справдi, якщо ми маємо дiло зi складним повiдомленням, що полягае в одночасному повiдомленнi двох фактiв Aii Вj, i якщо цi факти (подiї) незалежнi в iмовiрносному розумiннi, то, згiдно (1. 14),

I (A, Bj) = logP (AiÇBi).

Або, застосовуючи теорему про множення iмовiрностей, маємо

I(Аi,Bj) = - log[ Р(Аi)Р(Bj)] = -1оg Р(Ai) - log P(Вj) = I(Ai) - I(Bj). (1.16)

Іншими словами, кiлькiсть iнформацiї, вкладеної в два незалежних повiдомлення, рiвна сумi кiлькостi iнформацiї, вкладеної в кожне повiдомленнi. З наведеного вище визначення власної iнформацiї (1. 14) слiдує надто важливий висновок: з деяким повiдомленням Аiможна зв'язати поняття власної iнформацiї тiльки в тому випадку, якщо iснує поняття iмовiрностi цього повiдомлення (тобто, якщо його можна зв'язати з деяким статистичним ансамблем). Наприклад, окреме повiдомлення, не зв'язане з якою-небуть рiзноманiтнiстю, не володiє в розумiннi теорiї iнформацiї поняттям власної iнформацiї.

Можуть зустрiтися повiдомлення, що хоча i утворюють статистичну рiзноманiтнiсть, але не володiючi iмовiрнiстю внаслiдок нестационарностi випадкового механiзму. Наприклад, якщо ми пiдкидуємо абсолютно тверду монету, то випадковий механiзм випадання орла або решки стацiонарний, i обидва повiдомлення - випадання орла або решки - володiють iмовiрнiстю, що в цьому випадку рiвна половинi. Якщо же ми будемо пiдкидувати м'яку монету, то випадання орла або решки також буде випадковою подiєю. Однак випадковий механiзм вже не буде стацiонарний внаслiдок деформацiї монети. При цьому частота випадення, наприклад орла (або решки), зi збiльшенням числа кидання не буде прагнути до певної межi. Значить, з таким випадковим процесом не можна зв'язати поняття iмовiрностi (тут не дiє закон великих чисел). Отже, такi подiї (повiдомлення) не володiють iнформацiєю в сенсi (1.14).

Ця обставина має цiлком ясний фiзичний зміст: якщо в основi появи повiдомленнi на входi деякого каналу зв'язку не лежить стацiонарний випадковий механiзм, тобто для них не iснує поняття iмовiрностi, то випадковiсть такого типу не може бути нiяк завбачена, i для таких повiдомлень заздалегiдь неможливо побудувати оптимальний канал зв'язку.

Коли ми говоримо про оптимальнiсть, то маємо на увазi погодження пропускної спроможностi каналу з кiлькiстю iнформацiї, укладеною в повiдомленнях, що надходять на вхiд канала.

Може виявитися, що нестационарнiсть випадкового механiзму пiдкоряється певному закону. В цьому випадку iмовiрнiсть появи повiдомлень буде функцiєю часу. Для таких повiдомлень має мiсце поняття власної iнформацiї, що в цьому випадку також буде функцiєю часу.

Нарештi, може трапитися, що з системою повiдомлень можна зв'язати поняття iмовiрностi i, значить, кожне повiдомлення володiє власною iнформацiєю, але ми не знаємо цих iмовiрностей. В такому випадку ми також спочатку нiчого не можемо сказати про кiлькiсть iнформацiї, що несе в собi те або iнше повiдомлення. I тiльки з течiєю часу, пiсля надходження на вхiд канала достатньо великої кiлькостi повiдомлень, збирається необхiдна статистика, що дозволяє встановити кiлькiсть iнформацiї, зв'язану з кожним повiдомленням.

В технiчному сенсi це означає, що не можна заздалегiдь сконструювати хорошу систему (принаймнi в планi лiнiї зв'язку). Але ми маємо можливiсть будувати, самонавчальну систему, що адаптується, що з течiєю часу, з'ясовуючи iстинну статистику розподiлу повiдомлень, тобто визначаючи кiлькiсть iнформацiї, зв'язане з тим або iншим повiдомленням, зможе себе змiнювати, покращувати. Наприклад (в граничному випадку), по якому-небуть каналу надходить весь час одне i те ж повiдомлення А. В цьому випадку система визначить, що Р (А)=1 i, отже, I=0. Значить, можна просто запам'ятати це повiдомлення, а канал зв'язку вимкнути. Це i буде простим прикладом адаптацiї.

Другим важливим поняттям є вiдносна iнформацiя одного повiдомлення Sjвiдносно iншого Ai. Сенс цього поняття полягає в тому, що надходження деякого факту (повiдомлення Sj) може змiнити статистичну рiзноманiтнiсть, зв'язану з повiдомленням Аi, i внаслiдок цього власну iнформацiю повiдомлення Аi. Змiна власної iнформацiї повiдомлення A_і, що виникла через надходження повiдомлення Sj, i називається вiдносною iнформацiєю повiдомлення Sjвiдносно Ai.

Нехай iмовiрнiсть повiдомлення Аiдо надходження повiдомлення Sjрiвна Р(Аi). Тодi кiлькiсть власної iнформацiї, укладеної в повiдомленя Ai, рiвне

I (Ai) = -log P(Ai).

Iмовiрнiсть повiдомлення Аi, пiсля надходження повiдомлення Sjбуде рiвна Psj(Аi), тобто являє собою умовну iмовiрнiсть Aiза умови, що Sjмає мiсце. При цьому кiлькiсть iнформацiї, що мiститься в надходженнi повiдомлення Ai, рiвна

I (Ai/Sj) = - log Psj(Ai).

Тодi по визначенню iнформацiя, що мiститься в Sjвiдносно Аi, рiвна змiнi (зменшенню) власної iнформацiї повiдомлення Ai:

Isj(Ai) = I(Ai) - I(Ai/Sj) = - log P(Ai)+ log Psj(Ai) = log(Psj(Ai)/P(Ai)). (1.17)

Це нове поняття вiдносної iнформацiї зв'язане не з iмовiрнiстю повiдомлення Sj, а зi змiстом цього повiдомлення, бо саме конкретний змiст повiдомлення Sj визначає умовну iмовiрнiсть подiї Аi(Psj(Ai)). Таким чином, вiдносна iнформацiя деякого повiдомлення Sjзв'язана саме з його змiстом, а не з його власною рiзноманiтнiстю, якої може i не бути. Таким чином, навiть з окремим повiдомленням, не зв'язаним з поняттям iмовiрностi, можна зв'язати поняття iнформацiї вiдносно iншої рiзноманiтностi, якщо воно цю рiзноманiтнiсть змiнює.

В протилежнiсть власнiй iнформацiї, вiдносна iнформацiя може бути не тiльки позитивною, але i негативною. Якщо Psj(Ai)> Р(Аi), то, згiдно (1.17), Isj(Аi) = 0; якщо Psj(Ai)<P(Ai), то Isj(Ai) <0. Нарештi, при Psj(Ai)=P(Ai) Isj(Аi)=0. Останнiй випадок означає, що повiдомлення Sjне змiнює рiзноманiтностi Aii, отже, не мiстить в собi iнформацiї вiдносно повiдомлення Ai. Повертаючись до основної iнформацiйної мiри, до виразу (1.14), легко бачити, що числова величина його залежить вiд вибору основи логарифмування. Звичайно в теорiї iнформацiї в якостi основи беруть число 2; тодi числова величина кiлькостi iнформацiї, укладеної в деякому повiдомленнi Ai, рiвна

Ii=log2Рi. (1. 18)

В подальшому викладеннi для спрощення письма ми будемо опускати в записi логарифма iндекс 2, маючи на увазi, що скрiзь, за винятком спецiально обумовлених випадкiв, ми будемо мати справу з логарифмом при цiй основi. Припустимо, ми отримали повiдомлення, iмовiрнiсть якого рiвна половинi. Тодi таке повiдомлення володiє кiлькiстю iнформацiї

Ii=log2(1/2) =1 двiйкова одиниця = 1бiт.

Отже, це повiдомлення володiє однiєю двiйковою одиницею iнформацiї (двiйковою тому, що в якостi основи логарифма прийняте число 2) або, як часто говорять, несе 1 бim iнформацiї (б - bit, binary digit). В якостi дiйкової одиницi iнформацiї, приймається та кiлькiсть iнформацiї, що полягає в повiдомленi про те, що вiдбулися одне з двох рiвноможливих подiй (наприклад, iнформацiя про те, що при даному пiдкидуваннi монети випав герб).

Уявимо собi далi, що деякий дослiд може закiнчитися одним з чотирьох рiвноможливих наслiдкiв. Тодi повiдомлення про те, що має мiсце деякий конкретний наслiдок, володiє iмовiрнiстю Pi=l/4. Вiдповiдно кiлькiсть iнформацiї в цьому повiдомленнi J = - 1оg(1/4)=2 бiт. Якщо ж ситуацiя дослiду настiльки невизначена, що може з'явитися будь-який з 64 рiвноможливих наслiдкiв, то кiлькiсть iнформацiї, укладеної в повiдомлення про деякий конкретний наслiдок, рiвна J = - log(1/64) = 6 бiт i т. д.

Вже з цих прикладiв видно, що кiлькiсть iнформацiї в даному конкретному повiдомленнi тим бiльша, чим бiльша невизначенiсть ситуацiї. Як побачимо нижче, iснує дуже тiсний зв'язок мiж iнформацiєю i невизначенiстю, i що кiлькiсть власної iнформацiї може служити мiрою невизначеностi ситуацiї.

На кiнець розглянемо приклад. По каналу зв'язку передається пятизначне двiйкове число так, що в кожному розрядi може стояти цифра 0 або 1 з рiвною iмовiрнiстю, i поява тiєї або iншої цифри в даному розрядi не залежить вiд цифр що стоять в iнших розрядах. Визначимо, яка кiлькiсть iнформацiї мiститься в деякому числi, що передається. Нехай для визначеностi дано число, що передає значення 10110. Тодi iмовiрнiсть появи даного числа Ai = Рi = (1/2)5(згiдно теоремi множення iмовiрностей). Легко бачити, що будь-яке число, що передається володiє тiєю ж iмовiрнiстю. Тодi кiлькiсть iнформацiї, укладена в кожне число, що передається, рiвна

I = - log Pi = - log (1/2)5= 5 бiт.

Вiдповiдно при передачi n-розрядного двiйкового числа, кiлькiсть iнформацiї на повiдомлення рiвна I = n бiт.

З прикладу видно, що при двiйковому кодуваннi повiдомлень дуже зручно застосовувати при обчисленнi кiлькостi iнформацiї логарифм з основою два.

1.2.1 Iнформацiйна ентропія

До цих пiр ми розглядали кiлькiсть власної iнформацiї, що мiститься в даному конкретному повiдомленнi Ai, i для нього ввели мiру iнформацiї (1. 14) Ii = - log Pi. Уявимо собi тепер, що в результатi проведення деякого дослiду можливi k рiзноманiтних повiдомлень (результатiв дослiду А1, А2,..., Ak). Цей дослiд ми повторюємо велике число раз (n), наприклад n раз передаємо повiдомлення з даної вхiдної системи, i нехай з цих повiдомлень (результатiв) А1повторюється m1раз, А2повторюється m2раз i т. д. Крiм того, нехай iмовiрностi повiдомлень А1, А2,..., Akвiдповiдно рiвнi Р1, P2,..., Рk. Тодi середня власна iнформацiя на одне повiдомлення буде рiвна сумi iнформацiї, подiлленої на кiлькiсть повiдомлень,що передаються, або середня власна iнформацiя на одне повiдомлення рiвна

(- m1logP1 - m2logP2-... -mklogPk)/n.

Очевидно, межа цього вираження при n®¥ рiвна

k

H = - S Pilog Pi, (1. 19)

бо в вiдповiдностi з законом великих чисел

при n®¥ lim (mi/n)=Pi.

Вираз (1.19) являє собою середню власну iнформацiю на одне повiдомлення (на один результат дослiду) i називається iнформацiйною ентропiєю ситуацiї (дослiду) або просто ентропією. Поняття ентропiї надзвичайно важливе в теорiї iнформацiї, i щоб яснiше уявити фiзичний сенс цiєї величини, розглянемо деякi властивостi ентропiї.

1. Ентропiя завжди додатня

Н ³ 0. (1. 20)

Дiйсно, 0 £ Pi £ 1, тому log Pi£0, тобто величина вiдємна. Отже, враховуючи знак мiнус в виразi (1. 19), кожний член цiєї суми буде додатнiм, а отже, i вся сума додатня.

2. Ентропiя рiвна нулю в тому i тiльки в тому випадку, якщо iмовiрнiсть одного з результатiв рiвна одиницi, а отже, iмовiрностi всiх iнших результатiв рiвнi нулю (нагадаємо, що P1+P2+... +Pk=1). Iншими словами, ентропiя рiвна нулю, тодi коли ситуацiя повнiстю визначена, тобто результат дослiду заздалегiдь передбачено.

Дiйсно, вираз (1. 19) являє собою суму додатніх величин, тому ця сума може бути рiвна нулю тiльки в тому випадку, коли кожний з її членiв Р log P рiвний нулю. Вираз Р logР рiвний нулю або при Р=1 (що очевидно, бо при Р=1 логарифм Р рiвний 0), або при Р=0. В останньому випадку має мiсце невизначенiсть, i щоб її розкрити, запишемо вираз Р logР в виглядi

PlogP= (logP)/(1/P).

Границя цього виразу рiвна межi вiдношення похiдної числiвника до похiдної знаменника

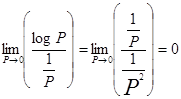
Але тiльки один результат дослiду може володiти iмовiрнiстю, рiвною одиницi, i при цьому всi iншi результатi володiють iмовiрнiстю, рiвною нулевi, тому сума (1. 19) рiвна нулю тiльки в цьому випадку i наше твердження доведене.

3. Ентропiя максимальна тодi i тiльки тодi, коли всi результати ситуацiї (дослiду) рiвноможливi. Припустимо, що наша ситуацiя може мати k результатов i всi вони рiвноможливi. Тодi Р1 = Р2.. = Рk = 1/k, оскiльки Р₁+P₂+...+Р_k=1. При цьому значення ентропiї в вiдповiдностi з (1. 19) буде рiвне

Hmax=log k. (1. 21)

Покажемо тепер, що ентропiя завжди менша або рiвна виразу (1. 21). Для цього складемо рiзницю

k

H - log k = - S Pilog Pi- log k =

k k k

= - S Pilog Pi- S Pilog k = - S Pilog 1/Pi,

1 1 1

k

оскiльки S Pi=1.

Скористаємось далi наступною властивiстю логарифмiчної функцiї: для будь-якого значення аргументу w має мiсце нерiвнiсть

ln w £ w-1. (1. 23)

Нерiвнiсть (1.23) (в лiвiй частинi стоїть натуральний логарифм) очевидно з рис. 5. Знак рiвностi має мiсце при значеннi w=1. Якщо в правій частинi (1. 22) величину 1/Рik позначимо через w i приймемо до уваги, що

log w = ln w log e,

то можна до кожного члена суми (1. 22) застосувати нерiвнiсть (1. 23). Тодi отримаємо

Оскiльки

то

H - log k £ 0 (1.24)

Таким чином, ентропiя завжди менша або рiвна величинi log k (1.22), причому знак рiвностi має мiсце при w=1, тобто при 1/Pik=1, або при всiх Pi=1/k, що означає рiвноможливiсть всiх результатiв дослiду.

З другої i третьої властивостей слiдує, що ентропiя рiвна нулю, коли ситуацiя повнiстю визначена, тобто результат дослiду заздалегiдь передбачено, i максимальна при найбiльшiй невизначенностi ситуацiї, коли всi можливi результатi дослiду рiвноможливi. Таким чином, ентропiя в принципі є мiрою невизначеностi ситуацiї i вона тим бiльша, чим бiльша ця невизначенiсть.

Всяке впорядкування ситуацiї, збiльшення її визначенностi зменшує ентропiю. Отже, вираз (1.19), з одного боку, являє собою середню iнформацiю, яку можна очiкувати вiд повiдомлення в даних умовах, а з iншого, його можна розглядати, як мiру невизначеностi ситуацiї.

Цi двi сторони, звичайно, зв'язанi мiж собою. Справдi, чим бiльш невизначена ситуацiя, тим бiльша iнформацiя буде полягати в кожному повiдомленнi про який-небуть конкретний результат. Часто в результатi деякого дослiду ми одержуємо деяку кiлькiсну величину х, що може приймати будь-яке значення в заданому iнтервалi. В цьому випадку результатом дослiду є безперервна випадкова величина, що володiє деяким законом розподiлу p (x) (рис. 6).

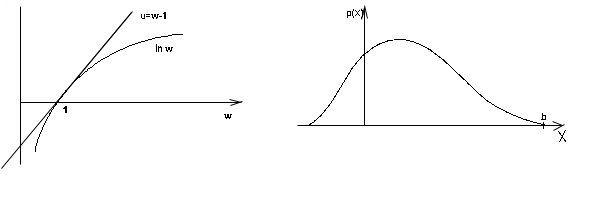
рис.5 рис.6

Отже, тут ми маємо дiло з нескiнченним числом можливих результатов i значить з нескiнченним числом можливих повiдомлень. Для такої ситуацiї по аналогiї з виразом (1.19) вводиться поняття ентропiї безперервного розподiлу

+¥

-ò p(x) log p(x) dx (1. 25)

-¥

Дата добавления: 2015-07-21