Формальный анализ исторических явлений.

1. Цель проекта

Установить, имело ли место в царской России на рубеже XIX-XX веков среди крестьянства серьёзное различие в материальном благосостояние и оказало ли оно влияние на ход революционных событий того времени, а также установить, была ли Россия капиталистическим или агарным государством на основе анализа ряда хозяйственно-экономических показателей того времени, представленных в Таблице 1.

Таблица 1

№	Губерния	Посев на душу (дес)	Лошади на дес. посева	Урожайность зерновых (пуд с дес.)	Продуктивный скот на душу населения
	Архангельская	0,19	0,66	55,6	0,4
	Астраханская	0,38	0,19	25,3	0,62
	Бессарабская	0,99	0,18	44,3	0,42
	Виленская	0,67	0,2	35,7	0,5
	Витебская	0,6	0,28	36,5	0,48
	Владимирская	0,57	0,22	40,2	0,28
	Вологодская	0,45	0,31	46,1	0,52
	Волынская	0,57	0,24	58,6	0,23
	Воронежская	0,89	0,17	38,8	0,44
	Вятская	0,99	0,18	42,7	0,44
	Гродненская	0,59	0,18		0,39
	Донская	1,55	0,18		1,07
	Екатеринославская	1,26	0,17	40,9	0,57
	Казанская	0,86	0,19	39,2	0,26
	Калужская	0,5	0,34	37,7	0,35
	Киевская	0,52	0,24	57,9	0,25
	Ковенская	0,61	0,28	44,1	0,51
	Костромская	0,64	0,24	42,7	0,37
	Курляндская	0,76	0,3	57,7	0,59
	Курская	0,87	0,21	43,5	0,29
	Лифляндская	0,66	0,28	62,6	0,57
	Минская	0,6	0,25	37,7	0,56
	Могилевская	0,56	0,41	39,6	0,43
	Московская	0,35	0,54	44,8	0,14
	Нижегородская	0,65	0,19	40,9	0,24

	Новгородская	0,48	0,37	43,1	0,44
	Олонецкая	0,37	0,42	57,6	0,5
	Оренбургская	0,94	0,29	34,2	0,64
	Орловская	0,81	0,22	41,7	0,26
	Пензенская	0,94	0,17	42,7	0,32
	Пермская	0,64	0,16	51,1	0,52
	Петербургская	0,42	0,59	46,3	0,1
	Подольская	0,66	0,32	43,8	0,42
	Полтавская	0,73	0,14	48,9	0,36
	Псковская	0,54	0,35	41,5	0,48
	Рязанская	0,75	0,19	45,1	0,31
	Самарская	1,14	0,25	30,6	0,48
	Саратовская	1,06	0,18	39,3	0,52
	Симбирская	0,91	0,17	41,2	0,29
	Смоленская	0,58	0,41	48,1	0,5
	Таврическая	1,95	0,14	35,9	0,55
	Тамбовская	0,88	0,18	50,9	0,33
	Тверская	0,5	0,38		0,41
	Тульская	0,9	0,2		0,3
	Уфимская	0,71	0,33	42,6	0,44
	Харьковская	0,9	0,16		0,41
	Херсонская	1,62	0,16	35,7	0,39
	Черниговская	0,69	0,29	34,3	0,33
	Эстляндская	0,56	0,3	61,6	0,52
	Ярославская	0,52	0,27	55,2	0,36

Данная таблица обладает только тем свойством, что названия губерний представлены в алфавитном порядке, а данные по количеству десятин посевной земли на душу населения, количеству лошадей на десятину посева, урожайности зерновых и продуктивного скота на душу населения представлены в хаотическом виде. Из этих хаотически представленных данных невозможно установить их влияние на ход исторических процессов в Европейской части России, а также установить наличие или отсутствие взаимосвязи между ними.

2. Теоретическая часть.

Известно, что историческая наука должна не только фиксировать во времени факты из жизни общества, но и устанавливать причинно – следственные связи, приводящие к тем или иным историческим явлениям.

По этому поводу известный русский историк В.О. Ключевский писал так: «В ходе человеческого общежития сменялись народы и поколения, …. изменялись порядки общежития, но нить исторического развития не прерывалась, … цивилизации чередовались последовательно, как народы и поколения, рождаясь одна из другой и порождая третью, … этот сложный процесс становится главным предметом изучения во всеобщей истории, прагматически, в хронологическом порядке и последовательной связи причины и следствия …» [1].

В рамках естественного языка причинно-следственные связи представляют цепь логически не противоречивых умозаключений. Однако, если в качестве причины берутся искажённые факты реальной действительности, то результат логического умозаключения будет неверен. Очевидно, что в таких случаях исторический прогноз социальных явлений будет ошибочен.

Такие ошибочные прогнозы имели место в русской истории. Так в [2] процитированы следующие мысли русского историка Роберта Виппера, высказанные в его книге «Кризис исторической науки» (1921).

«Напомнив выражение Цицерона: «история – наставница жизни», Виппер пишет так: Бывают эпохи, когда хочется сказать как раз обратное: не история учит понимать и строить жизнь, а жизнь учит толковать историю. Такую историю мы сами переживаем … Наши суждения о прошлом, наши исторические мнения приходится всё время пересматривать, подвергать критике и сомнению, заменять одни положения другими, иногда обратными. История из наставницы стала ученицей жизни … Мы были участниками, частицами великого государственного дела, ныне более несуществующего. Мы притягивали историю для объяснения того, как выросло русское государство и чем оно держится. Теперь факт падения России, наукой весьма плохо предусмотренный, заставляет историков проверять свои суждения. Он властно требует объяснения: надо найти его предвестие, его глубокие причины, надо неизбежно изменить толкование исторической науки.»

По поводу методов исследования исторических явлений в настоящее время там же в [2] сказано следующее.

«Безусловно, методология истории не замыкается на диалектике. Методика исследований совершенствуется, привлекаются методы других наук, расширяется, например, применение количественных методов в изучении исторических явлений, сравнительного анализа и т.п.»

Процесс анализа причинно – следственных связей должен основываться на количественных соотношениях, отражающих сущность исторических явлений. В таком случае указанный анализ будет беспристрастным, т.е. исключающем субъективизм того или иного исследователя.

Переход к беспристрастному анализу исторических фактов связан с их формализацией, т.е. установлению количественной меры того или иного явления и последующим представлением характера явления в форме математического закона.

Для иллюстрации принципа формализации исторических явлений рассмотрим ряд данных об аграрном и хозяйственном развитии 50 губерний Европейской России на рубеже XIX-XX веков (Табл. 1)

Для того, чтобы установить степень и характер влияния представленных данных на ход исторических процессов в Европейской части России на рубеже XIX-XX веков, а также выявить их возможную взаимосвязь, проведём формальный анализ каждого из 4х критериев, представленных в таблице 1 по следующему алгоритму, реализацию которого продемонстрируем на критерии «посев на душу населения».

Обозначим через x «посев на душу населения» и эту величину примем в качестве количественного признака губерний. Если сгруппировать губернии из таблицы 1 по числовым значениям этого признака, то после выявления общих исторических событий внутри сгруппированных указанным образом губерний можно установить влияние признака x, как причины тех или иных исторических событий.

Для дальнейшего анализа необходимо весь диапазон числовых значений x разделить на определённое число интервалов и с помощью данных таблицы 1 определить количество губерний, попадающих в каждый из интервалов.

В данном случае число интервалов можно выбрать равным десяти, а ширину интервала d будем определять по формуле (1), расчёт по которой в программе Excel определил d = 0,176.

(1)

Нижние и верхние границы указанных интервалов будем вычислять так:

, j = 0, 1, 2 … 9 (2)

Причём , а

Введём понятие статистического числа x_i как числа эквивалентного всем числам, попадающим в данный интервал, и его определим как середину выбранного интервала по следующей формуле

, j = 0, 1, 2 … 9; (3)

i = 1, 2 … 10

Вычисление частот p_i попадания губерний в i -ый интервал осуществляется по формуле:

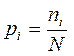(4)

Величины x_i и p_i представляют ряд распределения статистической величины x_i, т.е. таблицу значений этой величины и частоты p_i их появления. Указанный ряд распределения характеризуется математическим ожиданием:

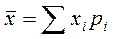(5)

и средним квадратическим отклонением равным:

(6)

В случае нормального закона распределения статистической величины x величина расположена посередине всего интервала изменения числовых значений x . В этом случае 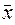есть в тоже время и наиболее вероятная величина.

Величина же определяет меру рассеяния величин x от наиболее вероятной величины 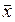. Кривая нормального закона обладает таким свойством, что для нее мера рассеяния определяется двумя точками на числовой оси, определяемыми как .

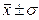Описанный выше анализ можно произвести с использованием программы MS Excel. Для этого напишем программу на языке макрокоманд. Так как любая программа требует отладки, будем проводить её посредствам сравнения получающихся в процессе написания программы результатов с образцами, представленными в виде рисунков.

1. Включение компьютера и вход в систему.

Параметры: - системный блок; - монитор.

Результат выполнения представлен на рисунке 1.

Рис. 1.

2. Запуск программы Microsoft Excel.

Параметры: - рабочий стол.

Результат выполнения представлен на рисунке 2.

Рис. 2.

3. Выбор активного листа.

Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 3.

Рис. 3.

4. Занесение заголовка в ячейку.

Параметры: - ячейка: A1; - данные: «№».

Результат выполнения представлен на рисунке 4.

Рис. 4.

5. Занесение заголовка в ячейку.

Параметры: - ячейка: B1; - данные: «Губерния».

Результат выполнения представлен на рисунке 5.

Рис. 5.

6. Занесение заголовка в ячейку.

Параметры: - ячейка: C1; - данные: «Посев».

Результат выполнения представлен на рисунке 6.

Рис. 6.

7. Автозаполнение - нумерация.

Параметры: - ячейка 1: «A1»; - ячейка 2: «A2»;

- конечная ячейка: «A51»; - данные 1: «1»;

- данные 2: «2»;

Результат выполнения представлен на рисунке 7. Рис. 7.

8. Занесение заголовка в ячейку.

Параметры: - ячейка: B2÷B51;

- данные: «Таблица1.Столбец2».

Результат выполнения представлен на рисунке 8. Рис. 8.

9. Занесение десятичных дробей в диапазон ячеек.

Параметры: - диапазон ячеек: С2¸С51;

- данные: « Таблица1.Столбец3 ».

Результат выполнения представлен на рисунке 9.

Рис. 9.

10. Активизация диапазона ячеек.

Параметры: - диапазон: B2÷C51. Результат выполнения частично представлен на рисунке 5.

Рис. 10.

11. Сортировка данных.

Параметры: - диапазон: B2÷C51; - тип: «по возрастанию»; - сортировка: «Посев». Результат выполнения частично представлен в таблице на рисунке 6.

Рис. 11.

12. Занесение формул в ячейку.

Параметры: - ячейка: D1; - данные: «=(C51-C2)/10». Результат выполнения представлен на рисунке 7.

Рис. 12.

13. Выбор активного листа.

Параметры: - лист: «Лист2». Результат выполнения представлен на рисунке 8.

Рис. 13.

14. Занесение заголовка в ячейку.

Параметры: - ячейка: A1, B1, C1, D1, E1, F1, G1, H1; - данные: «i», «y_i», «y_i+1», «x_i», «n_i», «p_i», «x_i*p_i», «p_i(x_i - )²». Результат выполнения представлен на рисунке 9.

Рис. 14.

15. Автозаполнение - нумерация.

Параметры: - ячейка 1: «A2»; - ячейка 2: «A3»;

- конечная ячейка: «A11»; - данные 1: «1»;

- данные 2: «2»; Результат выполнения частично представлен в таблице на рисунке 15.

Рис. 15.

16. Занесение десятичных дробей в ячейку.

Параметры: - ячейка: B2; - данные: «0,19».

Результат выполнения представлен на рисунке 16.

Рис. 16.

17. Автозаполнение – формула.

Параметры: - ячейка: « B3 »; - данные: «=$B$2+(Лист1!$D$1*Лист2!A2)»; - конечная ячейка: «B11». Результат выполнения частично представлен в таблице на рисунке 17.

Рис. 17.

18. Занесение десятичных дробей в ячейку.

Параметры: - ячейка: С2; - данные: «0,366».

Результат выполнения представлен на рисунке 18. Рис. 18.

19. Автозаполнение – формула.

Параметры: - ячейка: « С3 »; - данные: «=$C$2+(Лист1!$D$1*Лист2!A2)»; - конечная ячейка: «C11». Результат выполнения частично представлен в таблице на рисунке 19. Рис. 19.

20. Автозаполнение – формула.

Параметры: - ячейка: « D2 »; - данные: «=(B2+C2)/2»; - конечная ячейка: «D11». Результат выполнения частично представлен в таблице на рисунке 20. Рис. 20.

21. Специальная вставка – транспонирование.

Параметры:- диапазон: «С2÷C11»; - ячейка: « C13 ».

Результат выполнения представлен на рисунке 21.

Рис. 21.

22. Выбор активного листа.

Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 22.

Рис. 22.

23. Автозаполнение – формула.

Параметры: - ячейка: « E2 »; - данные: «=ЕСЛИ(Лист2!C$13>=Лист1!$C2;1;0)»; - конечная ячейка: «N51». Результат выполнения частично представлен в таблице на рисунке 23.

Рис. 23.

24. Автозаполнение – формула.

Параметры: - ячейка: « E52 »; - данные: «=СУММ(E2:E51)»; - конечная ячейка: «N52». Результат выполнения частично представлен в таблице на рисунке 24.

Рис. 24.

25. Автозаполнение – формула.

Параметры: - ячейка: « E53 »; - данные: «=E52-D52»; - конечная ячейка: «N53». Результат выполнения частично представлен в таблице на рисунке 25.

Рис. 25.

26. Специальная вставка – транспонирование.

Параметры:- диапазон: «E53÷N53»; - ячейка: « Лист2. E2 ».

Результат выполнения представлен на рисунке 26.

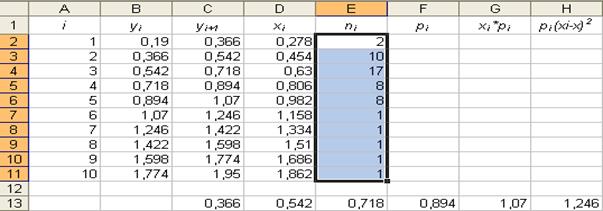
Рис. 26.

27. Занесение формул в ячейку.

Параметры: - ячейка: E12; - данные: «=СУММ(E2:E11)».

28. Автозаполнение – формула.

Параметры: - ячейка: « F2 »; - данные: «=E2/E$12»; - конечная ячейка: «F11». Результат выполнения частично представлен в таблице на рисунке 27.

Рис. 27.

29. Автозаполнение – формула.

Параметры: - ячейка: « G2 »; - данные: «=D2*F2»; - конечная ячейка: «G11».

30. Занесение формул в ячейку.

Параметры: - ячейка: G12; - данные: «=СУММ(G2:G11)».

Результат выполнения частично представлен в таблице на рисунке 28.

Рис. 28.

31. Автозаполнение – формула.

Параметры: - ячейка: « H2 »; - данные: «=F2*((D2-G$12)^2)»; - конечная ячейка: «H11».

32. Занесение формул в ячейку.

Параметры: - ячейка: H12; - данные: «=КОРЕНЬ(СУММ(H2:H11))».

Результат выполнения частично представлен в таблице на рисунке 29.

Таблица 2

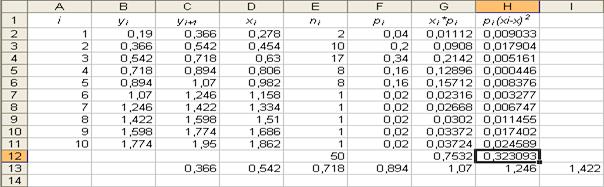
Рис. 29.

Из таблицы на рисунке 29 видно, что величина оказалась равной 0,7532 (ячейка G12), а - 0,3230 (ячейка H12).

Столбцы D и Е (рис. 29) позволяют табличный ряд распределения статистической величины представить графически в виде так называемого многоугольника распределения.

Для его построения продолжим написание программы на языке макрокоманд.

33. Построение диаграммы.

Параметры: - диапазон данных: «E2:E11»; - диапазон подписей: «D2:D11»;

- тип: « график »; - вид: « график с маркерами »; - название оси Х: « х_i »; - название оси Y: « p_i »; - название диаграммы: « Многоугольник распределения рассматриваемой случайной величины »; - размещение: «в отдельном листе »

Результат выполнения представлен на рисунке 30.

Рис. 30. Многоугольник распределения рассматриваемой

случайной величины.

Таким образом, получаем график (рис. 30), на котором по оси абсцисс отложена величина посева на душу в десятинах в губерниях Европейской части России, а по оси ординат – p_i, относительная величина числа губерний, обладающих признаком x .

Величина σ представляет диапазон 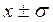, который определяет характер поведения частоты P_i в окрестности. Из многоугольника распределения статистической величины x_i можно увидеть, что получившийся график не является примером нормального распределения статистической величины по Гауссу.

Чтобы продолжить анализ нам необходимо преобразовать получившиеся данные, таким образом, чтобы можно было построить график нормального ряда распределения случайной величины по Гауссу.

Для этого выразим величину P_i = P_i(x_i) через эквивалентную ей величину P_i = P_i(z_i), где z_i – суть числа натурального ряда, которые поставлены в соответствие числам x_i. Таким образом, P_i = P_i(z_i) – суть дискретная функция, построенная на элементах z = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} дискретного множества.

После данной перенумерации получим дискретный ряд P_i = P_i(z_i), который имеет характерные свойства нормального ряда распределения случайной величины, т.е. числа P_i возрастают с ростом z до некоторого максимального значения, а потом убывают.

Теперь вычислим математическое ожидание и среднее квадратичное отклонение σ₁ по следующим формулам

(7)

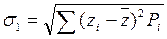(8)

Для сопоставления получившегося в результате преобразования ряд данных с теоретическим нормальным распределением Гаусса, вычислим для полученного рада данных критерий согласия распределений Пирсона - 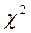по формуле

, (9)

где p_i – частота полученного в результате преобразования ряда данных, p_n – теоретическая частота каждого элемента z дискретного множества.

После чего построим график, отражающий взаимосвязь распределения частот ряда данных, полученных в результате описанного выше преобразования и теоретических частот каждого элемента z дискретного множества.

Для этого продолжим написание программы на языке макрокоманд и её отладки по посредствам сравнения получающихся в процессе написания программы результатов с образцами, представленными в виде рисунков.

34. Занесение заголовка в ячейку.

Параметры: - ячейка: A15, B15, C15, D15, E15, F15, G15, H15, I15, J15; - данные: «z_i», «x_i», «p_i», «x_i», «p_i», «z_i*p_i», «p_i(z_i - )²», «x-q», «x» «x+q». Результат выполнения представлен на рисунке 31.

Рис. 31.

35. Автозаполнение - нумерация.

Параметры: - ячейка 1: «A16»; - ячейка 2: «A17»;

- конечная ячейка: «A25»; - данные 1: «1»;

- данные 2: «2»; Результат выполнения частично представлен на рисунке 32. Рис. 32.

36. Активизация несвязанного диапазона ячеек.

Параметры: - диапазон ячеек 1: D2:D11; - диапазон ячеек 2: F2:F11. Результат выполнения представлен в таблице на рисунке 33.

Рис. 33.

37. Специальная вставка – значение.

Параметры: - ячейка: B16. Результат выполнения частично представлен на рисунке 30.

Рис. 30.

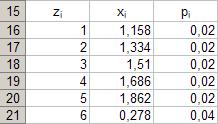38. Сортировка данных.

Параметры: - диапазон: B16÷C25; - тип: «по возрастанию»; - сортировка: «p_i». Результат выполнения частично представлен рисунке 31.

РРис. 31.

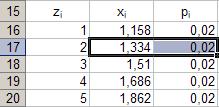39. Активизация диапазона ячеек.

Параметры: - диапазон ячеек: B17÷С17. Результат выполнения представлен в таблице на рисунке 32.

Рис. 32.

40. Копирование в буфер обмена.

Параметры: - ячейка-источник: «B17÷С17»; - ячейка-цель: «В16».

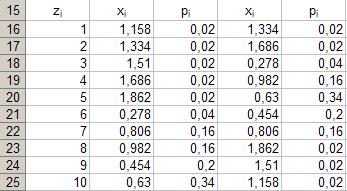Последовательно повторим выполнение пунктов 39 и 40 для всех оставшихся чётных диапазонов ячеек вплоть до диапазона B25÷C25. Вставку из буфера обмена следует производить последовательно в ячейки с D17 по D20. Рис. 33.

Аналогичным образом выполним шаги 39 и 40 для нечётных диапазонов ячеек начиная с диапазона B24÷C24 вплоть до диапазона B16÷C16. Вставку из буфера обмена следует производить последовательно в ячейки с D21 по D25. Результат выполнения представлен в таблице на рисунке 33.

41. Автозаполнение – формула.

Параметры: - ячейка: « F16 »; - данные: «=A16*E16»; - конечная ячейка: «F25».

42. Занесение формул в ячейку.

Параметры: - ячейка: F26; - данные: «=СУММ(F16:F25)». Результат выполнения пунктов 41-42 частично представлен в таблице на рисунке 34.

Рис. 34.

43. Автозаполнение – формула.

Параметры: - ячейка: « G16 »; - данные: «=E16*(A16-$F$26)^2»; - конечная ячейка: «G25».

44. Занесение формул в ячейку.

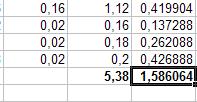Параметры: - ячейка: G26; - данные: «=КОРЕНЬ(СУММ(G16:G25))». Результат выполнения пунктов 56-58 частично представлен в таблице на рисунке 35.

Рис. 35.

45. Занесение формул в ячейку.

Параметры: - ячейка: H16; - данные: «=ОКРУГЛ(F26-G26;0)»; - ячейка: I16; - данные: «=ОКРУГЛ(F26;0)»; - ячейка: J16; - данные: «=ОКРУГЛ(F26+G26;0)». Результат выполнения представлен на рисунке 36. Рис. 36.

46. Занесение заголовков в ячейку.

Параметры: - ячейка: K15, L15; - данные: «p_n», «x²». Результат выполнения представлен на рисунке 37.

Рис. 37.

47. Автозаполнение – формула.

Параметры: - ячейка: « K16 »; - данные: «=НОРМРАСП(A16;F$26;G$26;0)»; - конечная ячейка: «K25».

48. Автозаполнение – формула.

Параметры: - ячейка: « L16 »; - данные: «=((E16-K16)^2)/K16»; - конечная ячейка: «L25».

49. Занесение формул в ячейку.

Параметры: - ячейка: L26; - данные: «=СУММ(L16:L25)». Результат выполнения шагов 47-49 представлен в таблице на рисунке 38.

Таблица 3

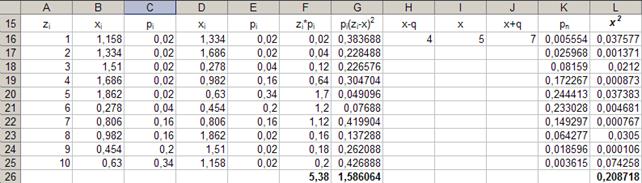
Рис. 38.

50. Активизация несвязанного диапазона ячеек.

Параметры: - диапазон ячеек 1: E16:E25; - диапазон ячеек 2: K16:K25. Результат выполнения представлен в таблице на рисунке 39.

Рис. 39.

51. Построение диаграммы.

Параметры: - диапазон данных: « E16:E25; K16:K25 »; - тип: « график »; - вид: « график с маркерами »; - название оси Х: « z_i »; - название оси Y: « p_i »; - название диаграммы: « Многоугольник распределения рассматриваемой случайной величины P_i = P_i(z_i)»; - размещение: «в отдельном листе »

Результат выполнения представлен на рисунке 40.

Рис. 40. Многоугольник распределения случайной величины P_i = P_i(z_i)

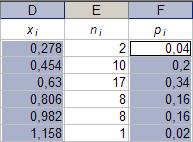
В результате проведенных вычислений получим ряд распределения P_i = P_i(z_i), который, в данном случае, определён на дискретной числовой оси z, поэтому чтобы полученные числовые параметры данного ряда распределения откладывать на числовой оси z_i их необходимо округлить, т.е. считать = 5, σ₁ = 4, σ₂ = 7.

По данным таблицы 3 построим многоугольник распределения слечайной величины z_i, а на числовой оси отложим числовые параметры = 5, σ₁ = 1, величина σ₁ определяет интервал , который характеризует рассеяние случайной величины z_i = z_i(x_i) от относительной максимальной частоты.

Из многоугольника распределения случайной величины на рисунке 42 видно, что в указанный интервал попадают точки z_i = 4, z_i = 5, z_i = 6 и z_i = 7. Дискретная функция z_i = z_i(x_i) определена в таблице 2. Из неё следует, что z_i = 4 соответствует значению x_i = 0,982, которое, согласно таблице 2 определяет диапазон посева на душу населения от 0,894 до 1,07; z_i = 5 соответствует значению x_i = 0,63, которое определяет диапазон посева на душу населения от 0,542 до 0,718; z_i = 6 соответствует значению x_i = 0,454, определяет диапазон посева на душу населения от 0,366 до 0,542; z_i = 7 соответствует значению x_i = 0,806, определяет диапазон посева на душу населения от 0,718 до 0,894.

Аналогично определим значения x_i, соответствующие точкам z_i, не вошедшим в указанный выше интервал, а также соответствующие им диапазоны посева на душу населения.

Программа Excel позволяет для указанных интервалов величины x из таблицы 1 выбрать названия губерний. Для этого в программе Microsoft Excel существует функция фильтрации с использованием автофильтра.

Воспользуемся автофильтром для проведения фильтрации. В качестве первого и второго условий фильтрации будем принимать значения указанных выше интервалов. Для проведения фильтрации напишем соответствующую программу на языке макрокоманд.

52. Выбор активного листа.

Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 43.

Рис. 41.

51. Активизация ячейки.

Параметры: - ячейка: C1.

52. Активизация автофильтра.

Результат выполнения представлен на рисунке 42.

Рис. 42.

53. Фильтрация с помощью автофильтра.

Параметры: - столбец: C; - первое условие: «значение больше или равно»; - значение: 0,894; - второе условие: «значение меньше»; - значение: 1,07. Результат выполнения представлен в таблице на рисунке 45. Рис. 43.

54. Копирование в буфер обмена

Параметры: - ячейка-источник: «B÷B»; - ячейка-цель: «Лист3.A2».

55. Выбор активного листа.

Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 44.

Рис. 44.

Аналогично, повторим выполнение макрокоманд 54-55 для остальных указанных выше интервалов. Скопированные в буфер обмена данные будем вставлять из буфера обмена в ячейки B2, C2 и D2 соответственно на «Лист 3». Результат представлен в таблице на рисунке 45.

Рис. 45.

56. Сохранение файла в сетевую папку.

Параметры: - сетевая папка: «//Public»; - имя файла: «Посев на душу населения.xls».

Для реализации целей проекта целесообразно разделить выполнение описанного выше алгоритма на отдельные этапы, которые будем называть блоками. В рамках каждого блока проекта будет проводиться анализ одного из перечисленных критериев, представленных в Таблице 1, причём, каждый блок будет выполняться независимо от других. Выполнение каждого блока будет проводиться автором, согласно Таблице 3. Каждый автор будет выполнять один блок проекта, после чего, полученные в результате выполнения каждым автором данные, могут быть объединены и использованы совместно, для формирования сводной таблицы отражающей результаты проекта в целом и реализацию его целей.

Таблица 3

Блок	Автор	Рассматриваемый в рамках блока критерий
Первый Блок		Лошади на десятину посева
Второй Блок		Урожайность зерновых (пуд с десятины)
Третий Блок		Продуктивный скот на душу населения

---

Дата добавления: 2015-07-21