Статистические методы прогнозирования.

Статистический прогноз основывается на знании общей тенденции и закономерностей развития явления за предпрогнозный период.

Процесс прогнозирования, опирающийся на статистические методы, распадается на два этапа.

Первый, индуктивный, заключается в обобщении данных, наблюдаемых за более или менее продолжительный период времени, и в представлении соответствующих статистических закономерностей в виде модели. Статистическую модель получают или в виде аналитически выраженной тенденции развития, или в виде уравнения зависимости от одного или нескольких факторов-аргументов, или в виде взаимосвязанных систем уравнений. Процесс построения и применения статистической модели для прогнозирования обязательно включает выбор формы уравнения, описывающего динамику или взаимосвязь явлений, и оценивание его параметров с помощью того или иного метода.

Второй этап, собственно прогноз, является дедукутивным. На этом этапе на основе найденных статистических закономерностей определяют ожидаемое значение прогнозируемого признака. Полученные результаты не могут рассматриваться как нечто окончательное. При их оценке и использовании должны приниматься во внимание факторы, условия или ограничения, которые не были учтены при разработке статистической модели.

Выделяют следующие методы статистического прогноза:

I. По среднегодовым абсолютным приростам или среднегодовым темпам роста – наиболее простой, но наименее надежный метод.

Пример: Выручка от реализации продукции за год составила (тыс.руб.): Январь – 100, Февраль – 112, Март – 116, Апрель – 135, Май – 140, Июнь – 124, Июль – 119, Август – 110, Сентябрь – 121, Октябрь – 140, Ноябрь – 153, Декабрь–158(рис.9.1)

Рисунок 9.1 - Динамика объема продаж

Средний абсолютный прирост за месяц составит:

= = где А_i – абсолютный прирост i-го периода

n – число периодов

Прогноз по среднему абсолютному приросту:

где t – период упреждения

i – номер последнего уровня исследуемого периода, за который рассчитан средний абсолютный прирост

Прогноз на январь следующего года = 158+5,3 = 163,3, на февраль = 158+2*5,3 = 168,6 и т.д.

Среднемесячный темп роста:

Прогноз по среднему темпу роста:

Прогноз на январь следующего года = 158*1,042 = 164,6, на февраль = 158*1,042² = 171,6 и т.д.

II. Экстраполяция полученной тенденции на основе уравнения тренда

По методологии, принятой в статистике, определяются вид и параметры уравнения тренда, оценивается ошибка тренда и ошибка прогноза. Прогноз дается в виде интервала.

Для определения линии тренда можно использовать статистические программы и табличный редактор Excel.

Пример: По данным предыдущего примера, используя возможности Excel, получим уравнение прямой y = 3,5315t + 104,38, ошибка аппроксимации данной модели 50,8%, что закономерно, т.к. динамика выручки, судя по рисунку 1, подвержена сезонности и более точно описывается рядом Фурье. (см. Статистика: национальные счета, показатели и методы анализа / под ред. Теслюка И.Е. – Минск: БГЭУ, 1995; Теория статистики /под ред. Шмойловой. – М.: Финансы и статистика, 1996)

Однако, возможности табличного редактора не позволяют получить ряд Фурье, поэтому при необходимости следует использовать более сложные специализированные статистические программы.

Уравнение прямой в общем виде может быть представлена следующей формулой:

где n – число анализируемых лет

t – порядковый номер года (1,2,…,n)

Для прогноза на перспективу необходимо подставить в уравнение порядковый номер прогнозного периода. Так как предпрогнозный период был представлен месячными данными за предыдущий год, то для нашего примера порядковый номер января – 13, февраля – 14.

Точечный прогноз на: январь = 3,5315*13+104,38 = 150,3; февраль = 3,5315*14+104,38 = 153,8

Однако, фактическая динамика, как видно на рисунке, отличается от выравненной. Следовательно, точечный прогноз может оказаться некорректным.

Для повышения точности прогноза следует построить прогнозный интервал, для чего необходимо определить ошибку прогноза. (см. Теория статистики./ под ред. Елисеевой, 1999).

В первую очередь определяют стандартную ошибку модели по следующей формуле:

где y_i, 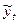– соответственно фактические и выравненные уровни

n – объем совокупности (число периодов)

р – число параметров модели прогноза (для прямой р=2, для параболы р=3 и т.д.)

Далее рассчитывается стандартная ошибка прогноза:

где к – период упреждения (порядковый номер периода, на который осуществляется прогноз)

По данным нашего примера рассчитаем ошибку прогноза. Ошибка модели также может быть определена с использованием функции “СТОШYX” EXCEL после расчета выравненных значений с помощью функции “ПРЕДСКАЗ”.

S_r = 13,14 = 24,51

Для расчета доверительных интервалов полученную ошибку прогноза умножают на t – критерий Стьюдента при заданной вероятности (a) и продолжительности предпрогнозного периода (n).

Таблица 9.1 - Выдержка из таблицы “Распределение Стьюдента”

n/a	0,1	0,05	0,02	0,01	0,001	n/a	0,1	0,05	0,02	0,01	0,001
	6,314	12,706	31,821	63,657	636,619		1,895	2,365	2,998	3,499	5,405
	2,920	4,303	6,965	9,925	31,598		1,860	2,306	2,896	3,355	5,041
	2,353	3,182	4,541	5,841	12,941		1,833	2,262	2,821	3,250	4,781
	2,132	2,776	3,747	4,604	8,610		1,812	2,228	2,746	3,169	4,583
	2,015	2,571	3,365	4,043	6,859		1,796	2,201	2,718	3,106	4,437
	1,943	2,447	3,143	3,707	5,959		1,782	2,179	2,681	3,055	4,318

Для выбора необходимой вероятности следует оценить устойчивость тренда по соответствующему коэффициенту.

где К_у – коэффициент устойчивости тренда

`y – среднее фактическое значение изучаемого показателя

По данным примера`y = 127,33, коэффициент устойчивости 10,32%. Следовательно, тренд достаточно устойчив и t-критерий можно принять с надежностью 0,90. Таким образом, границы прогноза составят:

для января - 150,3-1,782*24,51 у₁₃ 150,3+1,782*24,51

осуществив расчет, получим 106,62 у₁₃ 193,98

Аналогично рассчитываем для февраля - 110,12,62 у₁₄ 199,48

При рассмотрении квартальных или помесячных данных часто обнаруживаются определенные, постоянно повторяющиеся колебания, которые существенно не изменяются за длительный период времени. Такие колебания, которые имеют определенный и постоянный период, равный годовому промежутку, в статистике носят название “сезонные колебания” или “сезонные волны”. В этом случае более эффективным методом прогнозирования считается метод, базирующийся на аналитическом выравнивании по ряду Фурье.

Прежде чем использовать выравнивание по ряду Фурье, следует оценить наличие сезонных колебаний в динамике изучаемого показателя.

.Для этого используются следующие показатели:

1. Размах сезонных колебаний - это разность наибольшего и наименьшего значений показателя в течение анализируемого периода

2. Коэффициент сезонных колебаний представляет соотношение наибольшего и наименьшего значений показателя в течение года

3. Индексы сезонных колебаний характеризуют помесячные сезонные колебания и рассчитываются несколькими способами.

а) уровень каждого месяца сопоставляется со средним (или максимальным или минимальным в течение года) уровнем показателя

где `y – средняя, рассчитанная по фактическим значениям показателя за 12 месяцев, или средняя, исчисленная по выравненным теоретическим данным

б) если имеются помесячные данные за ряд лет, индексы сезонности рассчитываются вначале за каждый год по первому способу, а затем из индексов сезонности каждого месяца находят среднюю арифметическую за анализируемый период;

4. Обобщающим показателем величины сезонных колебаний является коэффициент вариации, который находится по следующей формуле:

где s– среднеквадритическое отклонение

`у_i - среднее значение признака за весь период (год)

где i_сез – индексы сезонности для i-го периода внутри года

Чем выше показатель вариации, тем более сильно выражены сезонные колебания признака, следовательно, тем более обоснованным является применение ряда Фурье.

По нашему примеру размах сезонных колебаний составил R = 158 (декабрь) – 100 (январь) = 58 тыс.руб. Коэффициент сезонных колебаний К_сез = 158 / 100 = 1,58 или 158%, что свидетельсвует о наличии значительных сезонных колебаний. Для расчета индексов сезонных колебаний вначале определим среднемесячное значение выручки:

`y = 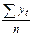= 1528/12 = 127,33.

Тогда индексы сезонности для каждого месяца составят (табл.9.2)

Таблица 9.2 - Индексы сезонности

Январь	100/127,33 = 0,78534	Июль	0,934555
Февраль	112/127,33 = 0,879581	Август	0,863874
Март	0,910995	Сентябрь	0,950262
Апрель	1,060209	Октябрь	1,099476
Май	1,099476	Ноябрь	1,201571
Июнь	0,973822	Декабрь	1,240838

Значения индексов сезонности показывает, что в январе, феврале, марте, июне, июле, августе поступления выручки были ниже среднемесячного годового значения, а в оставшиеся месяцы – больше. Среднеквадратическое значение составило s =17,1; коэффициент вариации v =13,4%.

Прогнозирование в данном случае, в самом простом варианте, осуществляется, исходя из последнего известного значения признака и полученных индексов сезонности.

Прогноз на январь = 158 (декабрь)* 0,78534 (индекс сезонности января) = 124,09.

Если каким-либо другим способом будет спрогнозировано среднемесячное значение показателя, то для каждого отдельного месяца объем выручки (по примеру) можно рассчитать путем умножения имеющегося среднего значения на индекс сезонности соответствующего месяца.

Например, среднемесячное значение в целом за год должно составить 215 тыс. руб., прогноз на январь: 215*0,78534 = 168,85

III. Прогнозирование на основе регрессионной модели

Подобный прогноз заключается в подборе факторов и оценке их влияния на формирование изучаемого показателя. Например, на объем выручки влияют цены реализации, объем продаж, рыночная конъюнктура, качество продукции и т.д. Путем статистической оценки силы взаимодействия выбранных факторов и результативного признака получают регрессионное уравнение.

Для прогнозирования в полученную модель подставляют плановые или желаемые значения факторных признаков и рассчитывают прогнозное значение результативного признака, отвечающее этим условиям.

Пример: зависимость объема предложения денег на финансовом рынке от выявленных факторов описывается следующим уравнением регрессии:

у = -151,8 – 2,5х₁ +1,5х₂ +0,74х₃

где у – предложение денег на финансовом рынке

х₁ – дефицит государственного бюджета

х₂ – кредитные вложения в экономику

х₃ – учетная ставка ЦБ

Подставляя прогнозные или желаемые значения факторов (дефицит, кредитные вложения, ставка), получим значение результативного признака (предложения денег). Если предусмотрено, что дефицит гос. бюджета сложится на уровне 1,5% от ВВП, ставка рефинансирования – 28%, а объем кредитных вложений в экономику – 245,5 млр. руб., то предложение денег на финансовом рынке составит: у = -151,8-2,5*1,5+1,5*245,5+0,74*28 = 233,42 млрд. руб.

IV. Прогнозирование на основе коэффициентов эластичности

Эластичность – это мера реагирования одной величины на изменение другой. Оценивается с помощью коэффициента эластичности:

где х₀, х₁ – значения факторного признака соответственно в базисном и отчетном периодах

у₀, у₁ – значения результативного признака соответственно в базисном и отчетном периодах

При значениях коэффициента эластичности больше 1 отмечается высокая эластичность, что свидетельствует о наличии связи между изучаемыми признаками.

В целях прогнозирования коэффициент эластичности может использоваться в том случае, если заранее известно изменение факторного признака. При этом будет прогнозироваться изменение результативного признака. Исходя из вышеописанной формулы изменение результативного признака равно:

Пример: Прибыль предприятия от реализации хлебобулочных изделий составила 386 и 250 тыс. руб. соответственно в отчетном и базисном периодах. Физический объем реализации за этот же период составил соответственно 48 тонн и 31 тонну. Определить объем прибыли в планируемом периоде при сохранении сложившихся пропорций, если физический объем реализации планируется довести до 52 тонн.

Кэ = (386-250)/(48-31):250/31 = 0,992

Dу_прог = 386/48*4*0,992 = 31,91 – на эту сумму увеличиться прибыль, следовательно прогнозная сумма прибыли составит 386+31,91 = 417,9 тыс.руб.

Дата добавления: 2015-07-21