
Читайте также:
|
Одним из основных направлений финансового анализа является оценка денежного потока Р1, Р2, Р3, …РW, генерируемого в течение ряда временных периодов в результате реализации какого-либо проекта или функционирования того или иного вида активов.
Ранее были рассмотрены методы приведения получаемых в разное время денежных потоков к одному временному периоду. При этом принималась во внимание некоторая единичная сумма – разовый поток. Однако, как известно, денежный поток может быть не только единичным, но и состоять из некоторых последовательных поступлений или выбытий денежных средств. В этом случае, алгоритмы расчета наращенной и приведенной стоимостей несколько отличаются от рассмотренных.
При общей постановке задачи, что имеется ряд платежей первоначальной стоимости с различной величиной членов Рi, выплачиваемых в течение n лет по ставке r, наращенная к концу срока сумма потока платежей методом прямого счета определяется как:
 - для простых процентов
- для простых процентов
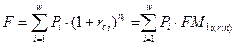 - для сложных процентов
- для сложных процентов
где i = 1…w - количество членов потока платежей.
Пример: График предусматривает следующий порядок выдачи ссуд во времени: 1 июля 2006г. – 5тыс.руб., 1 января 2007г. – 15 тыс., 1 января 2008г. – 18тыс. Необходимо определить сумму задолженности на начало 2009г. при условии, что проценты начисляются ежегодно по ставке 20%.
Схематично условия задачи можно изобразить так:
 5 15 18?
5 15 18?
t
1.06 1.01 1.01 1.01
2006 2007 2008 2009
Согласно условию примера, необходимо определить наращенную стоимость данного потока на 1.01.09. Оцениваем стоимость каждого члена потока и суммируем значения:
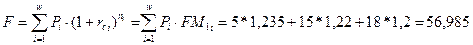
Наращенная сумма, полученная таким образом – это не что иное, как представление всех членов потока в виде одного числа, приуроченного к концу срока. В указанной формуле находит свое решение прямая задача оценки денежного потока. При этом, значения ставок процента, действовавших в отдельные периоды периода n могут совпадать, а могут и различаться.
Современная стоимость такого потока находят прямым счетом как сумму дисконтированных платежей. Современная стоимость потока платежей представляет собой его обобщающую оценку, приуроченную к началу операции:
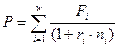 -для простых процентов
-для простых процентов
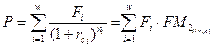 - для сложных процентов
- для сложных процентов
Между данными формулами сохраняется функциональная зависимость, которую мы уже отмечали:
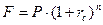
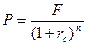

Продолжение примера:
Современная стоимость суммы долга на начало контракта (1.07.06г.) составит:
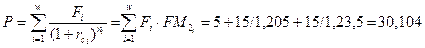
или 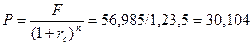
В главе 2 было рассмотрено, что денежный поток, в котором денежные поступления (или выплаты) в каждом периоде одинаковы по величине, называется финансовой рентой или аннуитетом. В связи с данной спецификой финансовых рент, расчет их будущей или дисконтированной стоимости несколько упрощается. При этом принимается во внимание вид ренты – постнумерандо (выплаты на конец периода) или пренумерандо (выплаты на начало периода).
Так как финансовая рента представляет собой поток платежей, состоящий из одинаковых членов, то в качестве первоначальной стоимости выступает размер отдельного платежа, который принято обозначать R.
Для решения прямой задачи оценки срочных аннуитетов постнумерандо (FRpst) и пренумерандо (FRpre) при заданных величинах регулярного поступления (R) и процентной ставке r используют следующие формулы:
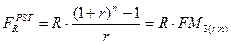
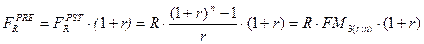
Экономический смысл показателя 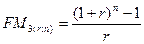 , называемого мультиплицирующим множителем для аннуитета (коэффициентом наращения ренты), заключается в следующем: он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу к концу срока его действия. Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Т.о., при оценке рент используются только сложные проценты.
, называемого мультиплицирующим множителем для аннуитета (коэффициентом наращения ренты), заключается в следующем: он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу к концу срока его действия. Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Т.о., при оценке рент используются только сложные проценты.
Пример: Для обеспечения некоторых будущих расходов создается фонд, средства в который поступают в виде постоянной годовой ренты постнумерандо (пренумерандо) в течение 5 лет. Размер разового платежа 4 млн.руб. На поступившие взносы начисляется проценты по ставке 18% годовых. Определить величину фонда на конец срока.
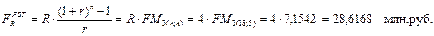
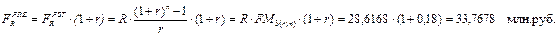
Для решения обратной задачи оценки срочных аннуитетов постнумерандо и пренумерандо, являющейся основой при анализе инвестиционных проектов, денежные притоки которых имеют вид аннуитетных поступлений, можно воспользоваться следующими формулами:
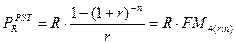
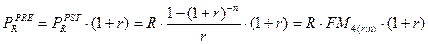
Экономический смысл показателя 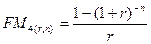 , называемого дисконтирующим множителем для аннуитета, заключается в том, что он показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы, продолжающегося n равных периодов с заданной процентной ставкой r.
, называемого дисконтирующим множителем для аннуитета, заключается в том, что он показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы, продолжающегося n равных периодов с заданной процентной ставкой r.
Между наращенной и современной стоимостью аннуитетов сохраняется указанная взаимосвязь: 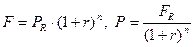 . При этом значения FR и PR определяются по вышеприведенным формулам.
. При этом значения FR и PR определяются по вышеприведенным формулам.
Если начисление процентов и\или выплаты членов ренты осуществляются чаще, чем один раз в год, используются следующие универсальные формулы. При этом количество начислений процентов в год (k) и выплат членов ренты (р) может как совпадать, так и не совпадать (к=р или к¹р):
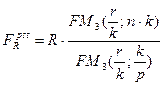
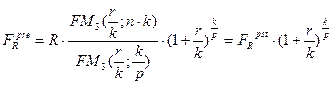
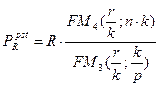
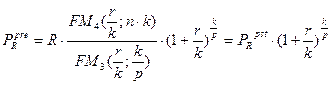
На основании рассмотренных формул можно вывести алгоритмы для расчета других параметров ренты.
Величина ежегодного платежа определяется:
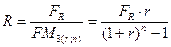 или
или 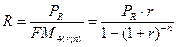
Для наиболее простого расчета срока ренты можно использовать следующие алгоритмы:
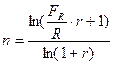
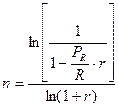
На практике часто встречаются случаи, когда члены потоков платежей изменяются во времени. Рассмотрим наиболее простой случай, когда члены денежного потока постнумерандо изменяются на постоянную абсолютную величину а.
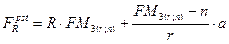
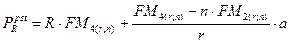
При этом, значение параметра а может быть как положительной, так и отрицательной величиной, что следует учитывать в виде соответствующего знака в формуле.
Пример: Оплата долгосрочного контракта предусматривает ежегодные выплаты в конце года. Первый платеж равен 15 млн.руб. Последующие платежи увеличиваются каждый раз на 2 млн.руб. Начисление процентов производится по ставке 20% годовых. Срок выплат 10 лет. Определим современную и наращенную стоимость денежного потока.
Табличные значения при сроке в 10 лет и ставке 20% равны: FM2(20;10) = 0,1615; FM4(20;10) = 4,192472; FM3(20;10) = 25,95868211 (см. приложение).
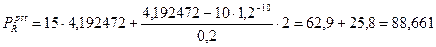
Зная, что 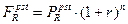 определяем наращенную стоимость аннуитета:
определяем наращенную стоимость аннуитета:
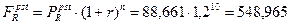
или 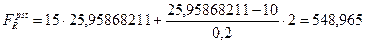
Второй вариант расчета наращенной стоимости ренты позволяет определить влияние каждого элемента потока, т.е. базового платежа и прироста. В нашем случае, постоянная рента с членом потока в 15млн.руб. дает накопление в сумме около 390 млн., при этом ежегодное увеличение члена рента на 2млн.руб. увеличивает наращенную стоимость на 160 млн.руб.
Рассмотренные формулы могут применяться и при условии систематического сокращения платежей.
Пример: Если по условиям предыдущего примера предполагается систематическое сокращение платежей на 1 млн. в год, то наращенная и дисконтированная стоимость составят:
FRpst= 15*25,95868211 +(25,9868211-10)*(-1)/0,2 = 389,380-79,793 = 30,587млн.руб.
PRpst= 15*4,192472 +(4,192472-10*1,2-10)/0,2*(-1) = 62,9-12,9 = 50млн.руб.
При решении задач по расчету первого члена ренты R или ее прироста а, необходимые значения находят из вышерассмотренных формул.
Для рент пренумерандо наращенная и дисконтированная стоимость для потока с изменяющимися членами находятся по формулам:
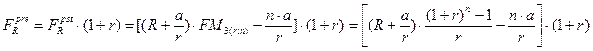
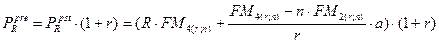
Если члены ренты изменяются согласно геометрической прогрессии, т.е. на постоянную относительную величину b, используются следующие алгоритмы расчета:
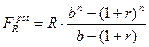
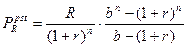
где b - темп изменения члена ренты (темп роста или темп снижения). Например, если член ренты ежегодно увеличивается на 3%, то b =1+0,03=1,03; если член ренты уменьшается на 3% в год, то b = 1-0,03=0,97
Пример: Предполагается, что плата за обучение, первоначально составляющая 20 тыс.руб. в год, будет увеличиваться на 10% ежегодно. Определите наращенную и современную стоимость такого потока платежей, если период обучения 5 лет, ставка доходности 5% годовых, а платежи осуществляются в конце периода.
Используя рассмотренные формулы, получим:
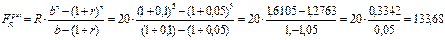 тыс.руб.
тыс.руб.
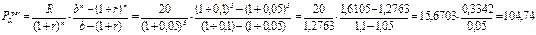 тыс.руб.
тыс.руб.
Вопросы для самоконтроля:
1. В чем заключается концепция временной стоимости денег?
2. Назовите факторы, определяющие неравноценность денежных потоков, полученных в различные периоды времени и дайте им характеристику.
3. Каким образом учитывается временной фактор при принятии финансовых решений?
4. Дайте определение процессам дисконтирования и компаудинга. В чем заключается их экономический смысл?
5. Что понимается под современной и наращенной стоимостями?
6. Дайте определение видам ставок доходности.
7. В чем различия между простыми и сложными процентами?
8. В рамках решения каких задач может проводиться оценка денежного потока?
9. В чем заключается экономический смысл мультиплицирующего и дисконтирующего множителей?
10. Что такое эффективная ставка, для чего она применяется? Что означает к-разовое начисление процентов?
11. Какие ставки называют эквивалентными?
12. В чем заключается экономический смысл показателей FM3(r;n) и FM4(r;n)?
Тестовые задания:
1. Факторы, определяющие неравноценность денежных потоков во времени:
1. рутинность, предосторожность, спекулятивность
2. метод учета выручки от реализации, способ начисления амортизации, способ оценки материалов
3. инфляция, риск, спекулятивность
4. инфляция, риск, возможность получения дохода
5. изменение покупательной способности денег, изменение валютного курса, изменение доходности финансового рынка
2. Впишите недостающие слова:
Временная ценность денег есть главнейшая …. характеристика денежных …, связанная с возможностью получения … от вложения средств в текущий момент и …. снижения их …. способности в результате … процессов в будущем.
3. В финансовых расчетах фактор времени учитывается 2 способами:
1. простым и сложным
2. наращением и дисконтированием
3. наращением и дефлятированием
4. индексацией и дисконтированием
5. дефлятированием и индексацией
4. Окончите предложение:
Смысл операций по учету временного фактора, заключается в …..
5. Эквивалентность будущих и текущих денежных сумм означает:
1. что они равны
2. что они генерируют одинаковый уровень доходности
3. что владельцу безразлично, иметь ли сегодня некоторую сумму денег, или через определенное время–ту же сумму, но увеличенную на величину процентов
4. что возможен обмен одной суммы на другую
5. что они равны и генерируют одинаковый уровень доходности
6. Окончите предложение:
Неравноценность денежных потоков разных временных периодов обусловлена влиянием таких факторов, как……..
7. Соотнесите характеристики и смысл показателей и процессов с их названием:
Название показателей Характеристика, экономический смысл
1. Современная стоимость а. Стоимость, рассчитываемая как сумма
всех членов потока платежей с
начисленными на них к концу срока
процентами
2. Компаудинг б. Процесс увеличения суммы денег в связи с
присоединением процентов в результате
проведения финансовой операции
3. Дисконтирование в. Процесс нахождения суммы,
эквивалентной будущей стоимости
денежных средств
4. Наращенная стоимость г. Стоимость, которая рассчитывается
путем суммирования всех членов потока,
дисконтированных на начало срока
финансовой операции
8. Сумма дохода от предоставления ссудного капитала в долг называется:
1. процентом
2. доходностью
3. маржой
4. прибылью
5. денежным потоком
9. По какой формуле определяется учетная ставка:
1. 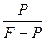 2.
2. 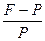 3.
3. 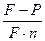 4.
4. 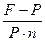 5.
5. 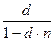
10. Прямая задача оценки денежных потоков заключается в:
1. реализации схемы дисконтирования
2. приведении членов денежного потока к некоторому начальному моменту времени
3. преобразовании выручки от реализации в чистую денежную прибыль
4. оценке с позиции настоящего
5. оценке с позиции будущего
11. 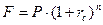 :
:
1. формула современной стоимости ренты
2. формула наращенной стоимости при начислении процентов n раз в году
3. формула наращенной стоимости для сложных процентов
4. формула наращенной стоимости для дисконтной ставки
5. формула наращенной стоимости аннуитета с изменяющимися членами
12. Экономический смысл какого процесса заключается в приведении будущих денежных потоков к настоящему времени:
1. дисконтирования
2. компаудинга
3. сложных процентов
4. дефлятирования
5. индексации
13. По какой формуле определяется сложная процентная ставка:
1. 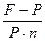 2.
2. 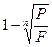 3.
3. 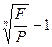 4.
4. 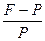 5.
5. 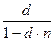
14. Какая годовая ставка дает тот же результат, что и к-разовое начисление процентов по ставке  :
:
1. простая
2. сложная
3. учетная
4. эквивалентная
5. эффективная
15. Как определяются формулы эквивалентности ставок:
1. через наращенную стоимость
2. путем приравнивания взятых попарно множителей наращения для конкретных условий
3. исходя из формулы эффективной ставки
4. путем приравнивания наращенных сумм
5. исходя из количества начислений процентов в год
16. Соотнесите название показателя с алгоритмом его расчета:
Название показателя Алгоритм расчета
1. Простая ставка дисконта а. 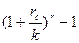
2. Сложная ставка процента б. 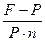
3. Сложная учетная ставка в. 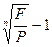
4. Простая процентная ставка г. 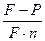
5. Эффективная процентная ставка д. 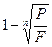
17. 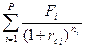
1. формула наращенной стоимости регулярного потока платежей (не ренты)
2. формула наращенной стоимости ренты
3. формула приведенной стоимости регулярного потока платежей (не ренты)
4. формула расчета члена ренты
5. формула современной стоимости потока платежей при начислении процентов чаще, чем 1 раз в год
18. Какой показатель является мультиплицирующим множителем для обычного аннуитета
1. 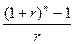 2.
2. 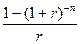 3.
3. 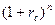 4.
4. 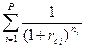 5.
5. 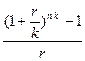
19. Формула для расчета наращенной стоимости ренты постнумерандо для любых условий выплат и начисления процентов:
1. 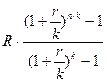 2.
2. 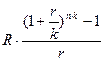 3.
3. 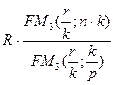
4. 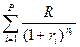 5.
5. 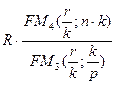
20. 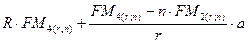
1. формула для расчета наращенной стоимости аннуитета с изменяющимися членами
2. формула для расчета наращенной стоимости ренты постнумерандо при начислении процентов к-раз в год
3. формула для расчета приведенной стоимости ренты с изменяющимися членами
4. формула для расчета современной стоимости регулярного потока R (не ренты)
5. формула для расчета срока ренты пренумерандо
21. Соотнесите название показателя с алгоритмом его расчета:
Название показателя Алгоритм расчета
1. Наращенная стоимость денежной а. 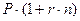
суммы по сложным процентам
2. Современная стоимость денежной б. F*FM2(r;n)
суммы по сложным процентам
3. Наращенная стоимость потока в. 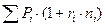
платежей по простым процентам
4. Наращенная стоимость ренты г. 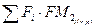
постнумерандо
5. Наращенная стоимость денежной д. R*FM3(r;n)
суммы по простым процентам
6. Современная стоимость е. P*(1+rс)n
ренты пренумерандо
7. Современная стоимость потока ж. R*FM4(r;n)*(1+r)
платежей по простым процентам
8. Наращенная стоимость потока з. 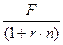
платежей по сложным процентам
9. Современная стоимость денежной и. 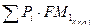
суммы по простым процентам
10. Наращенная стоимость денежной к. 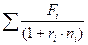
суммы при начислении процентов к-раз в год
11. Современная стоимость ренты л. 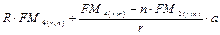
постнумерандо с изменяющимися членами
12. Современная стоимость потока м. 
платежей по сложным процентам
22. Банк выдает 100 тыс. руб. на 1 год под 10% годовых. При использовании дисконтной ставки клиент получит на руки и вернет через год соответственно:
1. 100 и 110 тыс. руб.;
2. 90 и 110 тыс. руб.;
3. 80 и 100 тыс. руб.;
4. 90 и 100 тыс. руб.
23. 10 тыс. руб. разместили в банк на 3 года, по истечении которых клиент получил 20 тыс. руб. Доходность операции в виде годовой простой процентной ставки составит:
1. 100%;
2. около 27%;
3. около 33%;
4. около 17%;
5. 50%.
24. 10 тыс. руб. разместили в банк на 3 года, по истечении которых клиент получил 20 тыс. руб. Доходность операции в виде годовой простой учетной ставки составит:
1. 100%;
2. около 27%;
3. около 33%;
4. около 17%;
5. 50%.
25. 10 тыс. руб. разместили в банк на 3 года, по истечении которых клиент получил 20 тыс. руб. Доходность за весь срок операции составит:
1. 100%;
2. около 27%;
3. около 33%;
4. около 17%;
5. 50%.
26. При вложении 100 тыс. руб. на 5 лет под 10% годовых клиент получит (соотнести результат с методом начисления % и видом применяемой ставки):
1. простая %-ставка а). 200 тыс. руб.
2. сложная %-ставка б). 161.1 тыс. руб.
3. сложный дисконт в). 169.4 тыс. руб.
4. простая учетная ставка г). 150 тыс. руб.
27. Определите результат вложений 120 тыс. руб. на 2 года под 12 % годовых начисляемых ежемесячно:
1. 124 тыс. руб.
2. 148.9 тыс. руб.
3. 152.4 тыс. руб.
4. 96.7 тыс. руб.
28. Определите самый доходный контракт:
1. ежемесячное начисление 12% годовых по процентной ставке;
2. ежемесячное начисление 24% годовых по процентной ставке;
3. ежемесячное начисление 24% годовых по дисконтной ставке;
4. ежемесячное начисление 12% годовых по учетной ставке.
29. В банк на 2 года под простую процентную ставку 10% при годовом начислении % положено 20 тыс. руб. Чтобы получить эквивалентный доход следует применить сложный процент при полугодовом начислении % в размере:
1. 9.2%;
2. 20%;
3. 10.8%;
4. 10%.
30. Значение множителя наращения ренты для 3 лет и 20% годовых составит:
1. 1.728;
2. 3.64;
3. 0.579;
4. 0.275.
31. Если множитель дисконтирования ренты постумерандо равен 0.65, а член ренты- 10 тыс. руб., то современная стоимость ренты составит:
1. 6.5 тыс. руб.;
2. 15.4 тыс. руб.;
3. 7.15 тыс. руб.;
4. 6.9 тыс. руб.
ТЕМА 7
Дата добавления: 2015-07-21; просмотров: 126 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Эквивалентность ставок доходности. | | | Влияние инфляции на финансовые инструменты. Оценка стоимости денег в условиях инфляции. |