Результаты освоения Учебной дисциплины

Студент должен обладать следующими общекультурными компетенциями (ОК):

- знаниями законов развития природы, общества, мышления и умением применять эти знания в профессиональной деятельности; умением анализировать и оценивать социально-значимые явления, события, процессы; владением основными методами количественного анализа и моделирования; теоретического и экспериментального исследования (ОК-4).

- способностью к формированию, поддерживанию и использованию конструктивных общефизических и социально-психологических ресурсов, необходимых для здорового образа жизни (ОК-17).

Студент должен обладать следующими профессиональными компетенциями (ПК):

- способностью адаптировать основные математические модели к конкретным задачам управления (ПК-23).

- способностью применять информационно-коммуникационные технологии в профессиональной деятельности с видением их взаимосвязей и перспектив использования (ПК-26).

В результате изучения дисциплины студент должен:

1) Знать: основы векторной алгебры и аналитической геометрии, теорию пределов, дифференциальное и интегральное исчисление, функции многих переменных, дифференциальные уравнения, числовые и функциональные последовательности и ряды, элементы теории функции комплексного переменного, теорию вероятностей и математическую статистику

2) Уметь: используя соответствующий математический аппарат решать примеры и задачи по темам, предусмотренным ООП дисциплины «математика», а также уметь использовать приобретенные знания для освоения дисциплин, обладающих содержательно-методической взаимосвязью с дисциплиной «математика» и обозначенных в пункте 2 настоящей программы.

3) Владеть общими принципами построения, исследования и использования математических моделей в управлении, экономике, финансах и маркетинге.

4.СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

Общая трудоемкость дисциплины составляет 5 зачетных единиц, 180 часов.

Структура учебной дисциплины

Таблица №1

№ п/п	Разделы (темы) учебной дисциплины	Семестр / подсеместр	Виды учебной деятельности, включая самостоятельную работу студентов и трудоемкость (в часах)	Формы текущего контроля успеваемости по темам.
			Лек -ции.	Прак. занят.	Само ст.раб.
	Раздел I. Элементы линейной алгебры и аналитической геометрии.
	Тема 1. Матрицы и определители.	2.2
	Тема 2. Системы линейных алгебраических уравнений.	2.2
	Тема 3. Векторная алгебра.	2.2
	Тема 4. Элементы аналитической геометрии.	2.2		-
	Раздел II. Введение в Математический анализ
	Тема 5. Основы теории множеств и математической логики.	2.2
	Тема 6. Понятие функции. Способы задания функции.	2.2	-
	Тема 7. Комплексные числа.	2.2	-
	Тема 8. Комбинаторика. Бином Ньютона.	2.2
	Раздел III. Теория пределов. Непрерывность
	Тема 9. Предел последовательности.	2.2
	Тема 10. Предел функции.	2.2
	Тема 11. Бесконечно малые и бесконечно большие величины.	2.2
	Тема 12. Непрерывность функции. Классификация точек разрыва.	2.2		-		.
	Раздел IV. Дифференциальное исчисление функции одного переменного
	Тема 13. Производная	2.2
	Тема 14. Дифференциал функции	2.2
	Тема 15. Производные и дифференциалы высших порядков.	2.2
	Тема 16. Применение производной.	2.2
	Итого за семестр	2.2				Тестирование.
	Раздел V. Интегральное исчисление функции одного переменного
	Тема 17. Неопределенный интеграл. Общие приемы интегрирования.	2.2
	Тема 18. Интегрирование рациональных дробей.	2.2
	Тема 19. Определенный интеграл и его приложения.	2.2
	Раздел VI. Функции многих переменных
	Тема 20. Функции многих переменных. Частные производные и дифференциал.
	Тема 21. Экстремум функции нескольких переменных.
	Раздел VII Дифференциальные уравнения
	Тема 22. Дифференциальные уравнения первого порядка. Задача Коши (обзор).
	Тема 23. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами (обзор).
	Раздел VIII. Элементы теории вероятностей и математической статистики
	Тема 24. Случайные события.
	Тема 25.Повторение испытаний.
	Тема 26. Случайные величины.
	Тема 27. Законы распределения случайных величин.
	Тема 28. Система случайных величин.
	Тема 29. Элементы математической статистики.
	Итого за семестр	2.3
	ВСЕГО

Итого 180 часов, в том числе 9 часов ИРС.

Форма итогового контроля: Экзамен.

СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

Раздел I. Элементы линейной алгебры и аналитической геометрии. Понятие матрицы. Сложение матриц, умножение матрицы на число. Произведение матриц. Квадратные матрицы. Транспонирование матриц. Определитель квадратной матрицы. Свойства определителей. Вычисление определителей второго и третьего порядка по правилу треугольника. Вычисление определителей n -ного порядка приведением к треугольному виду. Миноры и их алгебраические дополнения.. Вычисление определителей n -го порядка по правилу Лапласа (разложением по строке или столбцу). Невырожденная матрица, единичная матрица. Обратная матрица и правила ее отыскания. Ранг матрицы. Системы линейных алгебраических уравнений. Правило Крамера. Решение систем линейных алгебраических уравнений методом обратной матрицы. Метод Гаусса. Решение произвольных систем, теорема Кронекера-Капелли. Понятие об однородных системах и фундаментальной системе решений. Модель Леонтьева многоотраслевой экономики. Матрица прямых затрат. Уравнения межотраслевого баланса. Продуктивность матрицы прямых затрат.

Определение вектора. Коллинеарные и компланарные вектора. Равенство векторов. Линейные операции над векторами. Правило параллелограмма и треугольника. Базис. Разложение вектора по базису. Координаты вектора в данном базисе. Правая и левая тройка векторов. Ортонормированный базис. Правая и левая система координат. Декартова прямоугольная система координат. Координаты вектора в декартовой прямоугольной системе координат. Скалярное произведение векторов. Свойства скалярного произведения. Скалярное произведение векторов, заданных в ортонормированном базисе . Направляющие косинусы вектора 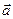. Проекция вектора на ось. Векторное произведение векторов, его свойства и геометрический смысл. Векторное произведение векторов, заданных в ортонормированном базисе . Смешанное произведение векторов. Двойное векторное произведение.

Прямая линия на плоскости. Уравнение прямой с угловым коэффициентом. Пучок прямых. Уравнение прямой, проходящей через две точки. Уравнение прямой в отрезках. Общее уравнение прямой. Нормальный вектор прямой. Взаимное расположение двух прямых. Угол между прямыми на плоскости. Нормальное уравнение прямой. Расстояние от точки до прямой. Плоскость. Общее уравнение плоскости, нормальный вектор плоскости. Взаимное расположение двух плоскостей в пространстве. Расстояние от точки до плоскости. Прямая линия в пространстве. Кривые второго порядка: эллипс, гипербола, парабола.

Раздел II. Введение в Математический анализ. Понятие множества. Подмножество. Равенство множеств. Пустое множество. Операции над множествами. Множества натуральных, целых рациональных и иррациональных чисел. Алгебраические и трансцендентные числа. Структура множества действительных чисел. Модуль действительного числа и его геометрический смысл. Свойства модуля. Основные понятия в множестве действительных чисел: сегмент, интервал, полуинтервал, ε -окрестность. Понятие расширенной системы действительных чисел и несобственного числа. Верхние и нижние границы числовых множеств. Ограниченные и неограниченные числовые множества. Множество комплексных чисел. Действия с комплексными числами в алгебраической форме. Тригонометрическая форма комплексного числа. Формула Эйлера. Показательная форма комплексного числа. Возведение в степень и извлечение корня из комплексного числа.

Высказывания. Операции над высказываниями. Необходимые и достаточные условия. Логические символы, правила построения отрицаний.

Сочетания, размещения перестановки и их свойства. Бином Ньютона, свойства биноминальных коэффициентов, треугольник Паскаля.

Понятия функции. Область определения и множество значений функции. Способы задания функции. График функции. Обратные тригонометрические функции. Преобразования графиков.

Раздел III. Теория пределов. Непрерывность. Определение числовой последовательности и ее предела. Единственность предела сходящейся последовательности. Ограниченность сходящейся последовательности. Арифметические операции с пределами последовательностей. Бесконечно малые и бесконечно большие последовательности. Монотонные последовательности. Свойства монотонных последовательностей. Подпоследовательности. Теорема Больцано-Вейерштрасса.

Определение предела функции по Коши и по Гейне. Арифметические операции с пределами функций. Односторонние пределы. Бесконечно малые величины. Главная часть бесконечно малой. Теорема о представлении бесконечно малой. Бесконечно большие величины.

Непрерывность функции в точке и на множестве. Арифметические свойства непрерывных функций. Классификация точек разрыва. Первая и вторая теоремы Вейерштрасса. Первая и вторая теоремы Коши для непрерывных функций.

Раздел IV. Дифференциальное исчисление функции одного переменного. Определение производной, ее геометрический и физический смысл. Таблица производных. Правила дифференцирования. Производные обратной и неявно заданной функции. Дифференциал функции и его геометрический смысл. Непрерывность дифференцируемой функции. Инвариантность формы первого дифференциала. Определение производной и дифференциала n -ного порядка. Основные теоремы дифференциального исчисления. Теорема Ролля. Теорема Коши для дифференцируемых функций. Теорема Лагранжа и ее геометрический смысл. Формула Коши. Правило Лопиталя. Формула Тейлора. Разложение основных функций по формуле Тейлора.

Условия монотонности функции. Экстремумы функции. Теорема Ферма. Необходимое условие экстремума. Достаточные условия экстремума. Выпуклые функции. Точки перегиба. Асимптоты графика функции. Полное исследование функций и построение графиков.

Раздел V. Интегральное исчисление функции одного переменного. Определение первообразной и неопределенного интеграла. Свойство неопределенного интеграла. Таблица интегралов. Основные методы интегрирования: метод разложения, внесение под знак дифференциала, замена переменной, интегрирование по частям. Понятие рациональной дроби. Простейшие рациональные дроби. Разложение рациональной дроби на простейшие. Интегрирование рациональных дробей.

Задачи, приводимые к понятию определенного интеграла: задача о нахождении площади криволинейной трапеции и задача о нахождении массы стержня. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла. Формула Ньютона-Лейбница. Интегрирование по частям и замена переменной в определенном интеграле. Вычисление площадей. Понятие о вычислении длин дуг и объемов тел вращения. Несобственные интегралы по бесконечному промежутку. Сходимость несобственных интегралов.

Раздел VI. Функции многих переменных. Определение функции двух и n переменных. Линии и поверхности уровня. Предел и непрерывность функции многих переменных. Теоремы о непрерывных функциях: первая теорема Вейерштрасса, вторая теорема Вейерштрасса, теорема Коши о промежуточных значениях. Определение частных производных. Дифференцируемые функции. Дифференциал. Частные производные и дифференциал высших порядков. Экстремум функции многих пременных. Необходимое условие экстремума. Достаточные условия экстремума. Условный экстремум (с ограничениями типа равенств). Метод подстановки. Функция Лагранжа. Метод неопределенных множителей Лагранжа. Определение градиента функции и его свойства. Определение производной по направлению. Связь производной по направлению и градиента.

Раздел VII. Дифференциальные уравнения. Определение дифференциального уравнения. Понятие об уравнениях в обычных и частных производных. Порядок дифференциального уравнения. Уравнения, разрешенные относительно производной. Определение решения дифференциального уравнения. Задача Коши и ее геометрическая интерпретация. Теорема существования и единственности и ее геометрический смысл. Уравнения с разделяющимися переменными.

Дифференциальные уравнения 2 -го и n -го порядка. Линейные однородные дифференциальные уравнения второго порядка (ЛОДУ). Теорема о структуре общего решения ЛОДУ. Характеристическое уравнение. Нахождение общего решения ЛОДУ по корням характеристического уравнения. Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами и структура его общего решения. Нахождение частного решения по виду правой части методом неопределенных коэффициентов.

Раздел VIII. Элементы теории вероятностей и математической статистики. Понятие случайного события. Невозможное и достоверное события. Сумма, произведение и разность событий. Противоположное событие. Полная группа событий. Полная группа попарно несовместимых событий. Классическое определение вероятности. Теоремы сложения и умножения вероятностей. Формула полной вероятности и формула Байеса. Последовательность независимых испытаний. Формула Бернулли и приближенная формула Пуассона. Теоремы Муавра Лапласа.

Дискретные и непрерывные случайные величины. Многоугольник распределения, ряд распределения. Функция распределения и ее свойства. Плотность распределения и ее свойства. Числовые характеристики случайных величин. Законы распределения и их числовые характеристики: закон равномерной плотности, биноминальный закон, закон Пуассона, экспоненциальный закон, нормальный закон.

Понятие многомерной случайной величины и закона ее распределения. Таблица (матрица) распределения двумерной дискретной случайной величины (X,Y). Условные распределения и условные вероятности одномерных составляющих двумерной случайной величины (X,Y). Функция распределения многомерной случайной величины и ее свойства. Плотность вероятности непрерывной двумерной случайной величины (X,Y) и ее свойства. Вероятность попадания двумерной случайной величины в заданную область. Числовые характеристики одномерных составляющих X и Y. Ковариация (корреляционный момент). Коэффициент корреляции.

Статистическое распределение выборки. Характеристики статистического распределения. Интервальные оценки. Эмпирическая функция распределения. Полигон и гистограмма. Выравнивание статистических рядов.

ПЛАН ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Дата добавления: 2015-07-20