Выбор подхода.

Для математического описания и получения статических характеристик ТОУ, выходная переменная которого зависит от многих входных переменных, наиболее совершенными являются экспериментально-статистические методы. Аппарат корреляционного и регрессионного анализов позволяет получить математическое описание объекта в виде полинома заданного вида, связывающего входные и выходные переменные в статическом режиме. Полученная зависимость называется уравнением регрессии.

Рис.47. Схема взаимодействия математических моделей объектов управления.

К математическим моделям объектов управления предъявляют ряд требований:

1) зависимости, описываемые моделью должны быть справедливы для всего расчетного интервала времени, на котором решается задача управления;

2) модель должна охватывать все входные переменные (управляющие, возмущающие воздействия), а также выходные (управляемые) величины.

При использовании теоретического подхода модель строится на основе соотношений, вытекающих из физических законов. При использовании формального подхода – на основе «вход–выходных» зависимостей (так называемом принципе «черного ящика»).

С целью накопления исходного статистического материала поставим пассивный эксперимент. Он основан на регистрации контролируемых параметров процесса в режиме нормальной эксплуатации работы объекта без внесения преднамеренных возмущений. Он экономически более оправдан и практически единственно возможен в том случае, когда испытаниям подвергается реальный промышленный объект с высокопроизводительным непрерывным производством дорогостоящего продукта. Если число опытов в пассивном эксперименте задано (например, из экономических соображений с учетом их стоимости), единственное, что можно сделать для увеличения точности регрессионной модели, это выбрать оптимальным образом интервал съема данных Δ t, который определяют из условия получения наиболее близкой к диагональной информационной матрицы с максимальным определителем. Для этого необходимо знать авто- и взаимную корелляционные функции случайных процессов ТОУ В частности, если при любых интервалах корреляции взаимная ковариация между переменными отсутствует, оптимальный выбор должен производиться из условия Δ t = max Δ _j, j= 1 ,k, где Δ _j - интервал корреляции (время затухания) процесса х_j (t), т.е интервал Δ t между соседними отсчетами был больше чем время затухания автокорреляционной функции самого "медленного" случайного процесса. Однако не имеет смысла делать Δ t много больше времени Δ _j, так как при этом продолжительность эксперимента существенно возрастает, а величины выборочных дисперсий практически не меняются.

Для оценки работоспособности полученной регрессионной модели часто вычисляют множественный коэффициент корреляции (характеризует тесноту связи между входными и выходной переменной), т е анализируют разность между единицей и величиной отношения дисперсии внешнего шума к выборочной дисперсии выходной переменной, рассчитанной относительно своего среднего значения. Можно считать регрессионную модель достаточно точной, если множественный коэффициент корреляции более .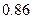

В моменты времени , ,..., , разделенные интервалом 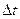будем измерять значения входных переменных , , , и выходных переменных , . Полученные данные будем использовать для нахождения оценок регрессионной модели и оценки дисперсии внешнего шума.

Проведем пассивный эксперимент и по полученным данным построим регрессионную модель ТОУ.

Дата добавления: 2015-07-20