Читайте также:
|
Для данного ТОУ мы имеем 2 случайных процесса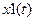 
и 
. Процессы 
и 
) являются случайными постольку, поскольку могут быть представлены как функции от 
и 
. Процессы 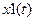и являются стационарными, т. к. они инвариантны относительно времени наблюдений. Чтобы охарактеризовать эти процессы необходимо знать их матожидание, дисперсию, автокорреляционную функцию.
Для оценивания автокорреляционной функции надо знать интервал корреляции 
Интервал корреляции – это время затухания автокорреляционной функции, когда она входит в некоторый достаточно малый коридор (в нашем случае этот коридор составляет 5%). Он может быть грубо оценен через соотношение 
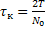, где 
– время протекания эксперимента, 
– количество пересечений графиком исследуемой функции прямой 
, где – рассчитанное среднее значение этой функции.
Существует 2 способа повлиять на сходимость автокорреляционной функции:
1. Изменение числа ординат;
2. Изменение времени снятия показаний (увеличение или уменьшение количества значений и, как следствие, информации о процессе).
Мы будем применять первый способ.
В итоге после нескольких экспериментов нам нужно получить уточненные значения коэффициентов корреляции, которые затем мы будем использовать для моделирования поведения контролируемых неуправляемых случайных величин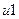 
и 
на следующих этапах исследования.
. 
Рис. 34 Предварительный эксперимент(260 значений.dat)
Рис. 35 Расчет аварийных ситуация и процента брака
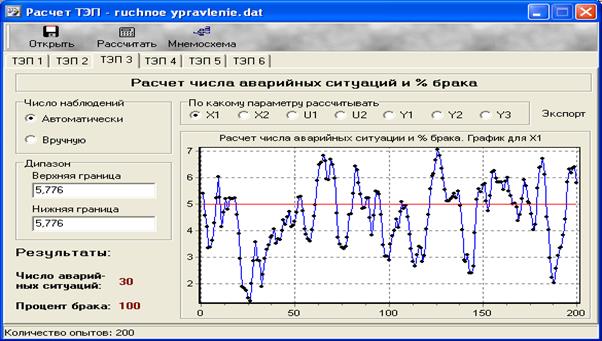
Рис. 36 Расчет числа пересечений с линей, соответствующей среднему значению
Определение коэффициента корреляции
При числе ординат равном 10
Рис. 37 Расчет числа пересечений с линей, соответствующей среднему значению
Определение коэффициента корреляции
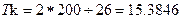
При числе ординат равном 10
Выбираем наименьшее значение. Оно равно 
Расчет количества значений: 
Рис. 38 Расчет среднего значения х2
Рис. 39 Статический анализ. Оценка математического ожидания и дисперсии. Для 17 ординат.
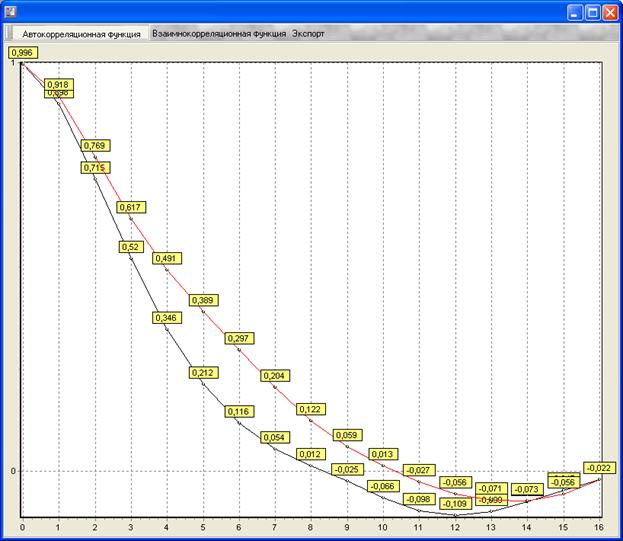
Рис. 40 Автокорреляционная функция. Для 17 ординат.
Рис. 41 Статический анализ. Для 5 ординат
Рис. 42 Автокорреляционная функция. Для 5 ординат
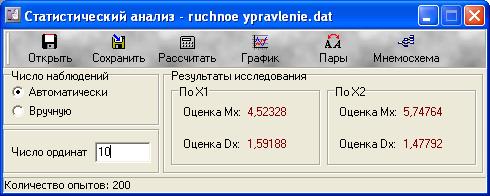
Рис. 43 Статический анализ. Для 10 ординат
Рис. 44 Автокорреляционная функция. Для 10 ординат
Рис. 45 Статический анализ. Для 15 ординат
Рис. 46 Автокорреляционная функция. Для 15 ординат
Дата добавления: 2015-07-20; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Нормальная эксплуатация с ручным управлением. | | | Выбор подхода. |