Состязания сигналов в последовательностных схемах

Принципиальная разница между комбинационными и последовательностными схемами заключается в том, что для последних рассматривают временные последовательности входных и выходных сигналов.

Однако вместо явно заданной переменной времени обычно ис­пользуют понятие состояния последовательностной схемы, считая, что ее выходной сигнал в любой момент времени t зависит от входного воздействия и состояния схемы также в момент времени t Состояние хранит информацию о прошлых входных воздействи­ях, подававшихся на последовательностную схему. Эта информа­ция запоминается в последовательностной схеме в виде внутренне­го сигнала или совокупности внутренних сигналов. Например, со­стояние счетчика указывает на количество поступивших считаемых сигналов.

Для того чтобы связать поведение последовательностной схемы с понятием состояния схемы, рассмотрим структурную модель асинхронной последовательностной схемы (рис. 7.8).

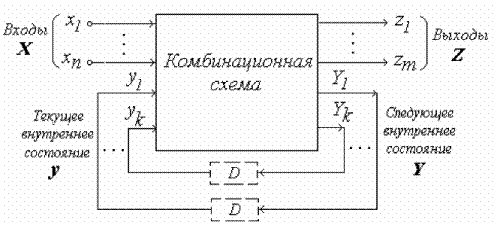
Рис. 7. 8. Структурная модель асинхронной последовательностной схемы

Она состоит из комбинационной схемы и обратных связей (ОС), каждая из ко­торых может содержать элемент задержки. Комбинационная схема имеет п - k входов, первые из которых являются входами всей схемы, а вторые — входами ОС.

Переменные y1, y2,...,yk,обозначающие входы ОС, называют внутренними переменными. Состояние входов ОС является внутренним состоянием последовательностной схемы в данный момент времени. Совокупность переменных х₁,х₂,...,х_n, y₁, y₂,...,y_k описывает полное состояние последовательностной схемы в дан­ный момент времени.

Выходами комбинационной схемы являются выходы всей схе­мы z_1, z₂,..., z_m и выходы ОС Y₁ Y₂,..., Y_k.

Если при неизменном состоянии входов X, сигналы на входе и выходе элементов задержки одинаковы, т.е. у = Y, то асинхронная последовательностная схема находится в устойчивом состоянии. При изменении состояния входов X может измениться один или несколько выходов Y комбинационной схемы. Таким образом, зна­чение выхода элемента задержки будет отличаться от значения его входов, т.е. у 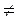Y. В этом случае схема находится в неустойчивом состоянии. Через промежуток, равный времени задержки, значения у изменятся и будут равны значениям Y. Если полученное полное состояние устойчиво, то сигналы на выходах Y комбинационной схемы больше изменяться не будут. Если же полное состояние не­устойчиво, то выходы Y будут изменяться до тех пор. пока не на­ступит устойчивое состояние. Отсюда ясно, что переменные Y опи­сывают внутреннее состояние асинхронной схемы в следующий момент времени.

Дата добавления: 2015-07-20