Синтез схем, свободных от статических состязаний

Комбинационная схема считается свободной от состязаний, если ее поведение не зависит от распределения задержек в цепях прохо­ждения сигнала. Будем рассматривать только переходы между па­рами смежных входных состояний, которые формируют одно и то же значение выхода.

Два входных состояния являются смежными, если они отли­чаются значением только одной переменной.

Обычно процесс разработки комбинационных схем начинается с нахождения минимальной ДНФ (КНФ) функции. При синтезе схем без статических состязаний необходимо несколько изменить про­цедуру отыскания выражения для функции. Если используется карта Карно, то необходимо на ней выбирать покры­тия таким образом, чтобы каждая пара смежных входных наборов, на которых функция равна 1 (или 0), входила хотя бы в одно по­крытие.

Рассмотрим функцию, занесенную на карту Карно (рис. 7.4). Минимальное выражение для этой функции:

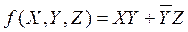
Комбинационная схема, построенная на элементах И-НЕ по этому выражению, приведена на рис. 7.1(a). В минимальном выра­жении функции два смежных входных состояния, помеченных на диаграмме буквами а и b (см. рис. 7.4), не входят в одно покрытие. Переход между этими состояниями и был рассмотрен выше (см. рис. 7.1(б)). Покрытие этой пары смежных входных состояний произведением XZ устраняет условия статического состязания.

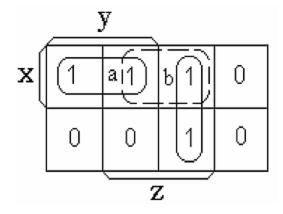
Рис. 7.4. Покрытие функции, необходимое для устранения

Дата добавления: 2015-07-20