Функциональные и логические состязания сигналов

Состязания в комбинационной схеме различают также в зависи­мости от количества входов, которые изменились при переходе от одного входного состояния в другое. Состязания, обусловленные одновременным изменением нескольких входных сигналов, отли­чаются от состязаний, возникающих при изменении одного входно­го сигнала, тем, что они не всегда могут быть устранены преобра­зованием выражения для функции. Если состязание возникает при одновременном изменении М входных сигналов, то в этом случае его называют М-состязанием.

Определение 3. Комбинационная схема содержит статическое М-состязание при одновременном изменении М входных сигналов, если:

• выходной сигнал перед изменением равен выходному сигналу после изменения входного состояния;

• во время переключения входных сигналов на выходе может появиться ложный импульс.

Существуют два различных типа статических М-состязаний. Первый тип, называемый функциональным состязанием, проиллю­стрируем с помощью карты Карно, изображенной на рис. 7.6.

Допустим, входное состояние изменяется от X = 1, Y = 1, Z = 0 (состояние "а") к Х= 1, Y = 0, Z = 1 (состояние "с"). Если измене­ние переменной Z произойдет быстрее, чем изменение переменной Y, то временно наступит промежуточное состояние "b" (X= Y = Z = = 1). Так как на данном наборе функция равна 0 (см. рис. 7.6), то на выходе схемы может появиться нулевой ложный импульс.

Пусть переход из состояния входов А к входному состоянию В осуществляется изменением т переменных, т.е.

где ai представляет собой значение 0 или 1 входной переменной xi.

Рис. 7.6. Иллюстрация функционального состязания

Определение 4. Комбинационная схема содержит функцио­нальное состязание при переходе из А в В, если для булевой функ­ции, которую реализует схема, справедливы два условия:

1) f(A)=f(B) и

2) существуют единичные и нулевые значения функции в 2^т-клетках подкуба (a_m+1,…,а_n).

Очевидно, что если схема содержит функциональное состязание при переходе из А в B, то должен быть некоторый набор для изме­няющихся переменных х₁..., х_т для которого функция не равна f(A), f(B). Следовательно, существует возможность такого распре­деления задержек в схеме, при котором входные изменения дости­гают выхода в последовательности, вызывающей ложные импуль­сы. Данное состязание является внутренне присущим функции и не может быть устранено ее преобразованием, если допускается изме­нение входных сигналов в произвольном порядке.

Второй тип статических М-состязаний, называемый логически­ми состязаниями, похож на статические состязания в том, что оба типа состязаний могут быть устранены с помощью выбора подхо­дящего выражения, используемого для построения схемы.

Определение 5. Комбинационная схема содержит логическое состязание при переходе из А в В, если справедливы следующие ус­ловия:

1) f(A)=f(B),

2) все 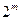значений функции f в подкубе (a_m+1... ,а_n) одинако­вы,

Дата добавления: 2015-07-20