Тоже на минимум

Если в сходной ЗЛП система ограничений в матричной форме имеет вид , то в двойственной ЗЛП она примет вид

!

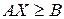
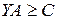
Если в исходной ЗЛП система ограничений в матричной форме имеет вид 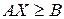, то в двойственной ЗЛП она примет вид

!

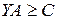
Пары двойственных задач называются симметричными, если в исходной задаче система ограничений задана в виде

!системы неравенств

системы уравнений

матричного уравнения

векторного уравнения

Пары двойственных задач называются несимметричными, если в исходной задаче система ограничений задана в виде

системы неравенств

!системы уравнений

матричного неравенства

векторного неравенства

В симметричной паре двойственных ЗЛП условие неотрицательности

накладывается только на исходные переменные

накладываются только на двойственные переменные

!накладывается и на исходные, и на двойственные переменные

не накладывается

В несимметричной паре двойственных ЗЛП условие неотрицательности

!накладывается только на исходные переменные

накладывается только на двойственные переменные

накладывается и на исходные, и на двойственные переменные

не накладывается ни на исходные, ни на двойственные переменные

Если целевая функция одной из пары двойственных задач не ограничена, то другая

имеет решение

!не имеет решения

имеет единственное решение

имеет бесконечное множество решений

Если система ограничений ЗЛП имеет вид , то в начальном опорном плане базисными переменными являются

Дата добавления: 2015-07-20