Нулевой

При получении решения системы уравнений с помощью симплексных преобразований количество итерации равно

количеству переменных

количеству ненулевых элементов разрешающего столбца

количеству нулевых элементов разрешающей строки

!количеству базисных переменных

Если при симплексных преобразованиях разрешающий элемент находится в строке с номером и в столбце с номером k, то новые значения правых частей уравнения подсчитываются по формуле

!

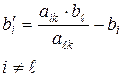
Если при симплексных преобразованиях разрешающий элемент находится в строке с номером и в столбце с номером k, то новое значение вычисляется по формуле

!

Решения систем линейных уравнений, которые принимают неотрицательные значения называются

недопустимыми

!допустимыми

нулевыми

нормальными

Совокупность всевозможных допустимых решений системы линейных уравнений называется

областью определения

областью решений

!областью допустимых решений

множеством неизвестных

Последовательное применение симплексных преобразований позволяют определить все

отрицательные решения системы

!опорные решения системы

нулевые решения системы

действительные решения системы

Указать среди базисных решений опорное

!

Указать вариант, в котором свободные члены системы уравнений могут являться результатом симплексных преобразований, если до них они были неотрицательными

(-2, 5, -6, -4)

(-1, 3, 4, -6)

!(4, 5, 7, 3)

(3, -2, 5, 1)

Какое количество опорных решений не может соответствовать перечисленным ниже числам, если число базисных решений равно десяти

!11

Если все свободные члены системы неотрицательны, то после каких преобразований они останутся неотрицательными

нормальных

!симплексных

прямых

обратных

Решения систем линейных уравнений называются допустимыми, если они принимают

отрицательные значения

нулевые значения

!неотрицательные значения

бесконечные значения

Если система уравнений приведена к единичному базису и при этом ее свободные члены неотрицательны, то соответствующее системе решение является

нулевым

!опорным

нормальным

обратным

При симплексных преобразованиях в качестве разрешающего уравнения выбирается то уравнение, для которого отношение свободного члена к положительному элементу разрешающего столбца

наибольшее

!наименьшее

равно нулю

больше нуля

Система уравнений приведена к единичному базису. Ее решение является опорным, если свободные члены

отрицательные

нулевые

!неотрицательные

неположительные

Указать вариант, в котором свободные члены систем уравнений не могут являться результатом симплексных преобразований, если до них они были неотрицательными

!(2, -5, 6, -4)

(1, 3, 2, 6)

(4, 1, 5, 3)

(3, 2, 5, 1,)

При каком преобразовании разрешающий столбец выбирается так, чтобы он имел хотя бы один положительный элемент?

при обратном

!при симплексном

при нормальном

при прямом

В качестве какого уравнения выбирается уравнение системы, для которого отношение свободного члена к положительному элементу разрешающего столбца наименьшее

нормального

линейного

!разрешающего

нелинейного

Если система уравнений приведена к единичному базису и при этом хотя бы один из ее свободных членов отрицательный, то соответствующее системе решение не является

нормальным

!опорным

базисным

обратным

Указать среди базисных решение, которое не является опорным

!

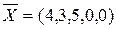
Переход от одного опорного решения к другому называется

однократной заменой

!однократным замещением

однократной перестановкой

однократным перемещением

При симплексных преобразованиях разрешающая строка отыскивается по правилу

!

Если в i – м уравнении системы линейных уравнений все , , то система не имеет

частных решений

базисных решений

общих решений

!неотрицательных решений

Симплексные преобразования применяются для отыскании неотрицательных

векторов

определителей

!решений системы уравнений

коэффициентов системы уравнений

Дата добавления: 2015-07-20