Линейно независимой

Если – линейно зависимая система векторов, а (r£n) - такая ее линейно независимая подсистема векторов, к которой нельзя присоединить ни одного вектора системы, не нарушив линейной независимости, то эта подсистема называется

минимальной линейно независимой

!максимальной линейно независимой

минимальной линейно зависимой

максимальной линейно зависимой

Всякая система векторов, содержащая нулевой вектор является

линейно независимой

нелинейно зависимой

нелинейно независимой

!линейно зависимой

Число векторов, входящих в любую максимальную линейно независимую подсистему векторов, называется

порядком системы

размером системы

!рангом системы

числом системы

Максимальное число линейно независимых векторов системы равно рангу матрицы , составленной

!из компонент векторов этой системы

из квадратов компонент этой системы

из кубов компонент этой системы

из квадратных корней компонент этой системы

Рангом системы векторов называется число векторов, входящих в любую

максимальную линейно зависимую подсистему

!максимальную линейно независимую подсистему

минимальную линейно зависимую подсистему

минимальную линейно независимую подсистему

Максимальное число линейно независимых строк матрицы равно

минимальному числу линейно независимых столбцов матрицы

минимальному числу линейно зависимых столбцов матрицы

максимальному числу линейно зависимых столбцов матрицы

!максимальному числу линейно независимых столбцов матрицы

Любая совокупность n+1 векторов n–мерного векторного пространства

!линейно зависима

линейно независима

образует базис

нелинейно независима

Максимальное число линейно независимых строк матрицы

равно размерности этой матрицы

!рангу этой матрицы

числу строк этой матрицы

числу столбцов этой матрицы

Базисом n–мерного векторного пространства называется любая совокупность

n+1 линейно независимых векторов этого же пространства

n-1 линейно независимых векторов этого же пространства

n(n-1) линейно независимых векторов этого же пространства

!n линейно независимых векторов этого же пространства

Любой вектор n–мерного векторного пространства можно представить как

нелинейную комбинацию векторов базиса

!линейную комбинацию векторов базиса

сумму векторов базиса

произведение векторов базиса

Система 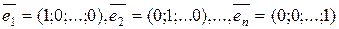называется системой

нулевых векторов n–мерного векторного пространства

зависимых векторов n –мерного векторного пространства

!единичных векторов n–мерного векторного пространства

независимых векторов (n+1)–мерного векторного пространства

называется

высотой вектора

шириной вектора

размером вектора

!длиной вектора

Числа , определяющие вектор , называются

числами вектора

!компонентами вектора

номерами вектора

неизвестными вектора

Любой вектор n–мерного пространства можно представить как линейную комбинацию векторов базиса

множеством способов

n способами

n-1 способами

!единственным образом

Рангом матрицы A называется число r такое, что у матрицы существует

!хотя бы один отличный от нуля минор r–го порядка и равны нулю все миноры более высокого порядка(³r+1)

хотя бы один отличный от нуля минор r+1–го порядка и равны нулю все миноры более высокого порядка

не более одного отличного от нуля минора r–го порядка и равны нулю все миноры более высокого порядка

не более одного отличного от нуля минора r+1–го порядка и равны нулю все миноры более высокого порядка

Если r-ранг матрицы А, то отличный от нуля минор r–го порядка называется

основным минором матрицы

минимальным минором матрицы

!базисным минором матрицы

ненулевым минором матрицы

Дата добавления: 2015-07-20