
Читайте также:
|

!!!!!!!!!!!!!!!!!! 
! 

При решении прямой ЗЛП решение двойственной задачи в симплекс – таблице с оптимальным планом получается
на пересечении столбца свободных членов и строки оценок
на пересечении последнего столбца и строки оценок
!на пересечении строки оценок и столбцов, соответствующих начальному базису ЗЛП
на пересечении первой строки и столбцов, соответствующих начальному базису ЗЛП.
Если i – е ограничение прямой ЗЛП обращается в строгое неравенство, то соответствующая компонента двойственной задачи 
не равна нулю
!равна нулю
положительна
отрицательна
Если j – е ограничение двойственной задачи обращается в строгое неравенство, то соответствующая компонента прямой ЗЛП 
отрицательна
положительна
не равна нулю
!равна нулю
Если одна из пары двойственных задач обладает оптимальным планом, то другая
!имеет оптимальное решение и 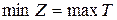 или
или 
не имеет решения и  или
или 
имеет оптимальное решение и  или
или 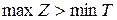
не имеет решения и 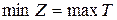 или
или 
Если исходная ЗЛП имеет вид  ,
,  ,
,  , то целевая функция симметричной двойственной задачи имеет вид
, то целевая функция симметричной двойственной задачи имеет вид
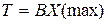
! 


Если исходная ЗЛП имеет вид  ,
, 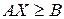 ,
,  , то целевая функция симметричной двойственной задачи имеет вид
, то целевая функция симметричной двойственной задачи имеет вид
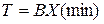
! 


Если исходная ЗЛП имеет вид  ,
,  ,
,  , то ограничения симметричной двойственной задачи имеют вид
, то ограничения симметричной двойственной задачи имеют вид

! 


Если исходная ЗЛП имеет вид  ,
, 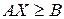 ,
,  , то ограничения симметричной двойственной задачи имеют вид
, то ограничения симметричной двойственной задачи имеют вид
! 



Опорным планом ЗЛП называется
неотрицательное решение системы ограничений
базисное решение системы ограничений
неотрицательное решение целевой функции
!базисное неотрицательное решение системы ограничений
Если множество наряду со своими точками содержит и отрезок, соединяющий любые его две точки, то оно называется
вогнутым
!выпуклым
полным
ограниченным
Множество планов ЗЛП
полно
вогнуто
!выпукло
не ограниченно
Если при решении ЗЛП на максимум для некоторого фиксированного j найдется оценка  , то опорный план является
, то опорный план является
оптимальным
!неоптимальным
отрицательным
недопустимым
Дата добавления: 2015-07-20; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| На пересечении строки оценок со столбцом первоначального базиса | | | Тоже на минимум |