Теорема Гаусса
Электрический заряд. Закон сохранения электрического заряда. Проводники, диэлектрики, полупроводники. | Закон сохранения электрического заряда. Проводники, диэлектрики, полупроводники. | Электрическое поле и его характеристики. Закон Кулона. Электрическое поле точечного заряда. Принцип суперпозиции. | Модели заряженных тел. | Два заряженных тела взаимодействуют между собой с силами, пропорциональными произведению этих зарядов и обратно пропорциональны квадрату расстояния между ними. | Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. | Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность. | Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника. | Таким образом, при параллельном соединении электроемкости складываются. | При последовательном соединении конденсаторов складываются обратные величины емкостей. |
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка Δ S. Произведение модуля вектора 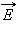 на площадь Δ S и на косинус угла α между вектором
на площадь Δ S и на косинус угла α между вектором 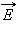 и нормалью
и нормалью 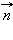 к площадке называется элементарным потоком вектора напряженности через площадку Δ S (рис. 1.3.1):
к площадке называется элементарным потоком вектора напряженности через площадку Δ S (рис. 1.3.1):
ΔΦ = E Δ S cos α = En Δ S
где En – модуль нормальной составляющей поля 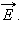
|
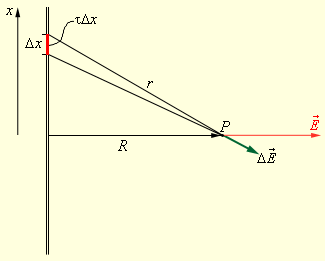
| Рисунок 1.20.
Электрическое поле заряженной нити
|
Дата добавления: 2015-07-20; просмотров: 61 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.009 сек.)

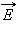 на площадь Δ S и на косинус угла α между вектором
на площадь Δ S и на косинус угла α между вектором 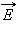 и нормалью
и нормалью 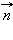 к площадке называется элементарным потоком вектора напряженности через площадку Δ S (рис. 1.3.1):
к площадке называется элементарным потоком вектора напряженности через площадку Δ S (рис. 1.3.1):