Принцип суперпозиции

Принцип суперпозиции: напряжённость результирующего поля находится путём определения геометрической суммы простых полей.

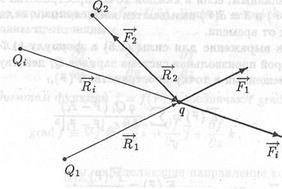
Рис.1.8. К формулировке принципа суперпозиции

Выражение, характеризующее принцип суперпозиции

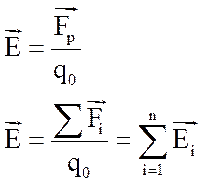(1.14)

Напряженность поля, как сила, действующая на пробный заряд, отнесенная к величине этого заряда, является количественной характеристикой поля

Рис.1.9. Сила, с которой заряд Q_i действует на пробный заряд q

(1.15)

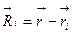
В соответствии с законом Кулона напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю

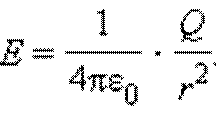
Это поле называется кулоновским. В кулоновском поле направление вектора 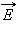зависит от знака заряда Q: если Q > 0, то вектор 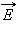направлен по радиусу от заряда, если Q < 0, то вектор 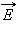направлен к заряду.

Для наглядного изображения электрического поля используют силовые линии. Эти линии проводят так, чтобы направление вектора 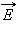в каждой точке совпадало с направлением касательной к силовой линии (рис. 1.10). При изображении электрического поля с помощью силовых линий, их густота должна быть пропорциональна модулю вектора напряженности поля.

Рис.1.10. Силовые линии электрического поля

По определению напряженности поля справедливы соотношения

(1.16)

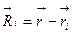(1.17)

- напряжённость поля точечного заряда q.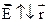

Для упрощения графического изображения векторного поля вводится параллельные линии вектора напряжённости (силовые линии). Линии напряжённости – линии, касательные к которым в каждой точке совпадают с вектором напряжённости.

Число линий, которое используется для изображения этого поля, численно равно значению напряжённости в данной точке.

Вектор касательной к силовым линиям и вектор напряженности коллинеарны(совпадают по направлению в точке приложения)(рис. 1.11).

Рис 1.11. Коллинеарность силовых линий

Линии напряжённости начинаются на положительных и отрицательных зарядах или уходит в бесконечность.

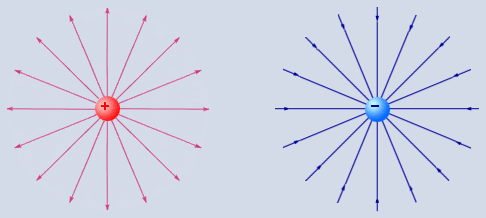
Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рис. 1.12. Так как электростатическое поле, создаваемое любой системой зарядов, может быть представлено в виде суперпозиции кулоновских полей точечных зарядов, изображенные на рис. 1.12 поля можно рассматривать как элементарные структурные единицы («кирпичики») любого электростатического поля.

Рисунок 1.12 Силовые линии кулоновских полей

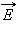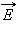Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор от заряда Q к точке наблюдения. Тогда при Q > 0 вектор параллелен а при Q < 0 вектор антипараллелен Следовательно, можно записать:

где r – модуль радиус-вектора .

Рис.1.13.Поле точечного заряда

Пример

Напряжённость электростатического поля.

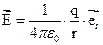- напряжённость поля, созданного точечным зарядом

Напряжённость электростатического поля суммы зарядов

(1.19)

В частности для двух зарядов(диполь)

Рис.1.14. Поле двух зарядов(диполь)

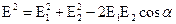
Для непрерывного распределения заряда суммирование определяется всеми зарядами в произвольной точке пространства:

- по всему объёму тела (1.20)

Пример. Напряженность равномерно заряженной нити

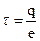, , -? (1.21)

точка О – начало отсчёта

(1.22)

(1.23)

Количество линий, пересекающих единичную перпендикулярную поверхность должно быть равно модулю вектора напряжённости.

Поток вектора напряжённости.

Количество линий напряжённости пронизывающих данную поверхность:

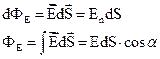(1.24)

(интеграл по поверхности)

Есл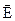и и 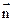= const, то

. (1.25)

Рис. 1.15. К определению потока вектора напряженности

Рис. 1.16. К вычислению потока напряженности поля точечного заряда через сферу

Диполь

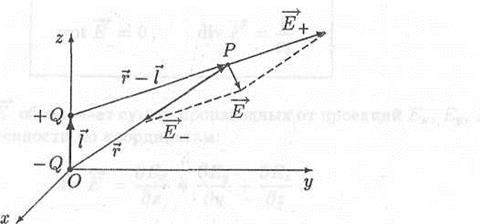
Электрический диполь – система из двух одинаковых по модулю зарядов разного знака q и – q, расположенных на некотором расстоянии l.

Рис.1.17. Поле двух зарядов(диполь)

В качестве примера применения принципа суперпозиции полей на рис. 1.18. изображена картина силовых линий поля электрического диполя.

Рисунок 1.18. Силовые линии поля электрического диполя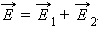

Важной характеристикой электрического диполя является так называемый дипольный момент

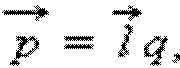
где 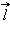– вектор, направленный от отрицательного заряда к положительному, модуль Диполь может служить электрической моделью многих молекул.

Электрическим дипольным моментом обладает, например, нейтральная молекула воды (H₂O), так как центры двух атомов водорода располагаются не на одной прямой с центром атома кислорода, а под углом 105° (рис. 1.19). Дипольный момент молекулы воды p = 6,2·10^–30 Кл · м.

Рисунок 1.19. Дипольный момент молекулы воды

Пример. Во многих задачах электростатики требуется определить электрическое поле 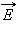по заданному распределению зарядов. Пусть, например, нужно найти электрическое поле длинной однородно заряженной нити (рис. 1.20) на расстоянии R от нее.

Поле в точке наблюдения P может быть представлено в виде суперпозиции кулоновских полей, создаваемых малыми элементами Δ x нити, с зарядом τΔ x, где τ – заряд нити на единицу длины. Задача сводится к суммированию (интегрированию) элементарных полей Результирующее поле оказывается равным

Вектор 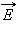везде направлен по радиусу Это следует из симметрии задачи. Уже этот простой пример показывает, что прямой путь определения поля по заданному распределению зарядов приводит к громоздким математическим выкладкам. В ряде случаев можно значительно упростить расчеты, если воспользоваться теоремой Гаусса, которая выражает фундаментальное свойство электрического поля.

Дата добавления: 2015-07-20