Сочетания с повторениями.

Для лучшего усвоения содержания проблемы рассмотрим следующую задачу. Имеется урна, содержащая n шаров. Предполагается, что все шары занумерованы от 1 до n. Выясним, сколько возможностей выбора соединений, содержащих m шаров, можно составить. При этом будем предполагать, что выборки отличаются друг от друга хотя бы одним элементом. Порядок элементов безразличен. В отличие от предыдущего случая будем предполагать, что после выбора каждого шара он снова возвращается в урну. Таким образом, соединения могут содержать повторяющиеся элементы (шары). Например, {3, 3, 2, 3} или {3, 4, 3, 3}. Такие соединения называются сочетаниями с повторениями или сочетаниями с возвращениями. Можно показать. что число сочетаний из n элементов по m имеет вид

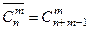
П р и м е р. Трое ребят собрали 63 яблока. Сколькими способами они могут разделить их между собой?

Р е ш е н и е. Поставим в соответствие каждому делению яблок между ребятами сочетание с повторениями следующим образом. Будем считать, что множество А = {a, b, c} (ребята). Следует составить сочетания с повторениями длины m = 63, n = 3. Таким образом, имеем три типа элементов, из которых надо составить соединения длины m = 63. Наличие в соединении какого-либо из элементов a, b, c означает принадлежность данного яблока соответствующему мальчику. Порядок элементов в таком соединении не играет роли. Число способов разделить яблоки между ребятами равно

Дата добавления: 2015-07-20