Поняття і параметри виробничої функції, її ізокванта та ізокоста

Сучасна теорія виробництва склалася наприкінці XIX – початку XX ст. У явному вигляді виробнича функція була представлена в 1890р. англійським математиком А.Беррі, який допомагав А.Маршаллу при підготовці математичного додатку до “Принципів економікс”.

Процес виробництва пов'язаний із споживанням різних ресурсів (факторів виробництва), які згідно з тією чи іншою технологією перетворюються на продукцію, яку випускають. Уособлені економічні одиниці, що здійснюють трансформацію факторів виробництва на продукти, називаються фірмами.

Для того щоб описати поведінку фірми, треба знати, яку кількість продукту вона може виробити, використовуючи ресурси у тих чи інших обсягах. При аналізі будемо виходити з припущення, що фірма виробляє однорідний продукт, кількість якого вимірюється в натуральних одиницях (тоннах, штуках, метрах і т. ін.). Залежність кількості продукту, яку може виробити фірма від обсягів витрат ресурсів, дістала назву виробничої функції.

Виробнича функція враховує тільки технічно ефективні варіанти. Технічно ефективними називають варіанти виробництва, які не можна покращити ні збільшенням виробництва продукту без зростання витрат ресурсів, ні скороченням витрат якого-небудь ресурсу без зниження випуску і збільшення витрат інших ресурсів.

Значення виробничої функції - це найбільша кількість продукту, яку може виробити фірма при даних обсягах споживання ресурсів.

Властивості виробничої функції:

1. При збільшенні витрат одного ресурсу, при незмінності інших відбувається збільшення обсягу виробництва продукції, але лише до певної межи.

2. Існує певна взаємозамінність та комплектарність факторів виробництва.

3. Зміни використання факторів виробництва менш еластичні в короткостроковому, ніж у довгостроковому періоді.

Двофакторна виробнича функція моделює виробничий процес, у якому змінним є обсяг використання двох факторів виробництва, але обсяг виготовленої продукції при цьому залишається незмінним. Тому більш реальною є виробнича функція виду:

q = f(x₁,х₂),

де q - величина випуску; x₁ і х₂ - витрати факторів виробництва.

Виробничу функцію даного виду неможливо зобразити на площині, вона може бути подана у тривимірному просторі. Дві координати (х₁ та x₂) відкладаються на горизонтальних осях, а третя (q) – на вертикальній осі і відповідає випуску продукту. Розглянемо цю ситуацію на рис. 2.1.1.

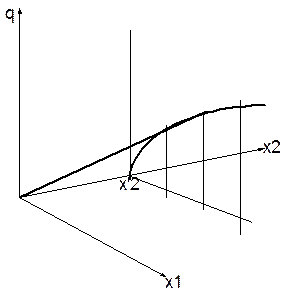
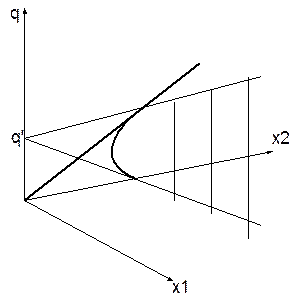
а) б)

Рис 2.1.1 – Виробнича функція у випадку двох ресурсів

Графіком виробничої функції служить поверхня "горба", що підвищується зростанням кожної з координат х₁ і x₂. При цьому графік на рис. 2.1.1. можна розглядати як вертикальний розріз «горба» площиною, паралельною осі х₁, що відповідає фіксованому значенню другої координати x₂= x'₂.

Якщо горизонтальний переріз поверхні «горба» зобразити окремо на площині з координатами х₁ і x₂, то буде крива, що об'єднує такі комбінації витрат ресурсів, які дозволяють отримати даний фіксований обсяг випуску продукту. Ця крива отримала назву ізокванти (isoquant) виробничої функції Вона подана на рис.2.1.2.

Ізокванта виробничої функції – це лінія, кожна точка якої відображає множинність усіх комбінацій кількості ресурсі, що відповідають різним ефективним способам виробництва заданого обсягу випуску продукції.

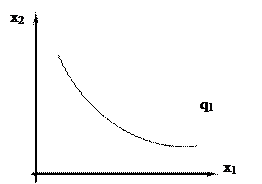Рис. 2.1.2 – Ізокванта виробничої функції

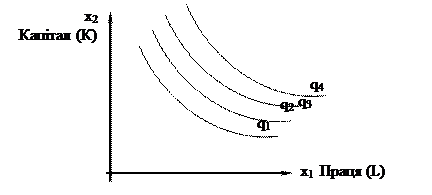Одну і ту ж кількість продукції можна отримати при різних поєднаннях витрат двох факторів (наприклад, праці та капіталу). Якщо зафіксувати обсяги випуску продукту на різних рівнях, одержимо ряд ізоквант тієї ж виробничої функції, тобто карту ізоквант (рис. 2.1.3).

Рис. 2.1.3 – Карта ізоквант

Безліч комбінацій ресурсів, витрати на купівлю яких однакові, графічно зображуються прямою, яка в теорії виробництва називається ізокостою виробничої функції (рис. 2.1.4). Їх нахил встановлюється співвідношенням цін:

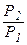або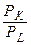

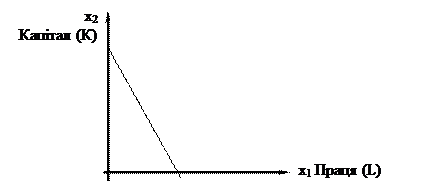Рис. 2.1.4 – Ізокоста виробничої функції

Ізокоста графічно відображує безліч усіх комбінацій ресурсів, які може придбати фірма за певну кількість грошей.

Зауважимо, що виробнича функція схожа на функцію корисності в теорії споживання, ізокванта – на криву байдужості, ізокоста – на бюджетну лінію. І справа тут не в простій схожості, бо за відношенням до ресурсів фірма поводить себе як споживач, і виробнича функція характеризую саме цей бік виробництва (виробництво як споживання).

Значення виробничої функції показує корисність для виробництва відповідного набору ресурсів. Виробнича функція є зростаючою функцією кожного із своїх аргументів і через кожну точку площини ресурсів з координатами х₁, х₂ проходить єдина ізокванта. Всі ізокванти мають негативний нахил. Ізокванта, що відповідає більшому виходу продукту розташована праворуч і вище ізокванти для меншого виходу. Усі ізокванти є випуклими в напрямку початку координат.

Теоретичний аналіз вимагає кожний вид ресурсу вважати абсолютно однорідним. Але сировина має різні сорти, машини різні марки, праця розрізняється професійно і за кваліфікацією. Тому більш реальною є виробнича функція значного числа аргументів, вона має вигляд:

q = f(x₁, x₂, …x_n).

Усе, що було сказано про виробничу функцію двох аргументів, можна перенести і на функцію значного числа аргументів із застереженням: ізокванти цієї функції – не плоскі криві, а n-мірні поверхні. Проте ми і в подальшому аналізі будемо користуватися «плоскими ізоквантами» – в ілюстративних цілях, і як зручним способом аналізу у випадках, коли витрати двох ресурсів є змінними, а інші – постійними.

Дата добавления: 2015-07-25