|
Читайте также: |
1. Разложите в ряд Фурье периодическую функцию 
с периодом 
, заданную на указанном сегменте.
а)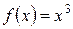 
, 
, 
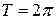; б)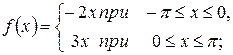 
.
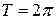2. Разложите в ряд Фурье периодическую функцию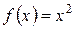 
с периодом 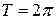на отрезке 
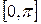. Продолжите на сегмент 
нечетным образом.
3. Разложите в ряд по синусам периодическую функцию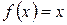 
с периодом 
на отрезке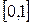 
.
4. Закончите выполнение ИДЗ №9.
5. Подготовьтесь к коллоквиуму.
Вопросы к коллоквиуму №3
Темы «Интегральное исчисление функции одной переменной. Ряды»
1. Первообразная функция, определение и теоремы.
2. Неопределенный интеграл и его свойства. Таблица основных интегралов.
3. Метод непосредственного интегрирования в неопределенном интеграле.
4. Метод замены переменной в неопределенном интеграле.
5. Метод интегрирование по частям для неопределенного интеграла. Классы интегралов, берущихся по частям.
6. Интегрирование рациональных выражений, содержащих квадратный трехчлен.
7. Интегрирование иррациональных выражений, содержащих квадратный трехчлен.
8. Интегрирование рациональных функций: сведение неправильных рациональных дробей к правильным, разложение дробно-рациональных выражений на простейшие дроби.
9. Интегрирование простейших рациональных дробей.
10. Интегрирование иррациональных функций: случаи сведения к интегрированию рациональных функций.
11. Применение подстановок Эйлера к интегрированию иррациональных выражений.
12. Интегрирование тригонометрических и других трансцендентных функций.
13. Интегралы, не выражающиеся в элементарных функциях.
14. Понятие об уравнении поверхности. Плоскость в пространстве. Различные уравнения плоскости: общее, в отрезках, нормальное. Уравнение плоскости, проходящей через три данных точки.
15. Прямая в пространстве. Прямая как линия пересечения двух плоскостей. Канонические уравнения плоскости. Параметрические уравнения плоскости. Приведение уравнений прямой к каноническим.
16. Угол между двумя плоскостями, между двумя прямыми, между прямой и плоскостью и их нахождение. Условия параллельности двух прямых, двух плоскостей, прямой и плоскости. Условия перпендикулярности двух прямых, двух плоскостей, прямой и плоскости.
17. Поверхности второго порядка: сфера, эллипсоид. Исследование их формы и построение.
18. Однополостный и двуполостный гиперболоиды. Исследование их формы и построение.
19. Эллиптический и гиперболический параболоиды. Исследование их формы и построение.
20. Цилиндрические и конические поверхности. Исследование их формы и построение.
21. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл как предел интегральных сумм.
22. Основные свойства определенного интеграла. Формула Ньютона-Лейбница.
23. Замена переменной и интегрирование по частям в определенном интеграле.
24. Приложения определенного интеграла для вычисления площади, длины дуги, площади поверхности вращения, объема.
25. Несобственные интегралы с бесконечными пределами интегрирования, интегралы от неограниченных функций.
26. Числовые ряды: основные понятия, необходимые условия сходимости ряда. Остаток ряда.
27. Ряды с положительными членами и признаки их сходимости: признаки сравнения, Даламбера, Коши (радикальный и интегральный).
28. Знакочередующиеся ряды, признак Лейбница.
29. Степенные ряды и область их сходимости.
30. Разложение функций в степенной ряд. Разложение некоторых элементарных функций (
, 
, 
, 
, 
, 
, 
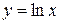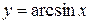) в ряд Тейлора (Маклорена).
31. Применение степенных рядов к приближенным вычислениям значений функций, интегралов, пределов.
32. Системы ортогональных функций. Примеры.
33. Тригонометрические ряды и их сходимость. Ряды Фурье. Формулы для вычисления коэффициентов ряда Фурье.
34. Ряды Фурье для четных и нечетных периодических функций.
Дата добавления: 2015-07-25; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задания, решаемые в аудитории | | | Для развития и контроля владения компетенциями |