Определите интервал сходимости ряда .

Решение. Воспользуемся признаком Даламбера. Выпишем -й и члены ряда: , . Тогда находим

- интервал сходимости ряда.

При ряд с положительным членами. Так как для любого натурального (, , ), следовательно, ряд расходится.

При ряд сходится, но условно.

Заметим, что так как среди коэффициентов данного ряда - нет равных нулю, то для нахождения радиуса сходимости можно было воспользоваться формулой 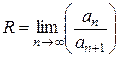. Тогда вычисляем

.

Следовательно - интервал сходимости.

5. Разложите в ряд Маклорена функцию .

Решение. Если функция на интервале разлагается в степенной ряд , то коэффициенты этого ряда определяются по формулам

, .

Подставляя выражения коэффициентов, получаем ряд

, (*)

который называется рядом Маклорена для функции .

Имеем откуда при получаем . Подставляя полученные числа в формулу (*), находим

Так как 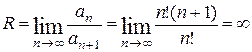, то ряд сходится на всей числовой прямой.

6. Разложите в ряд Маклорена функцию .

Решение. Воспользуемся разложением функции , полученным выше. Положим тогда . Имеем

.

При находим искомое разложение

,

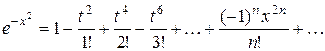которое справедливо, очевидно, для всех значений x.

7. Разложите в ряд Маклорена функцию

Решение. Имеем Используя формулу , запишем разложение функции заменив там на :

,

или

.

Таким образом,

.

Окончательно получаем

.

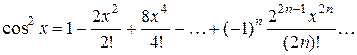Полученный ряд сходится при всех .

8. Разложите в ряд Маклорена функцию .

Решение. Имеем Воспользовавшись известным разложением ,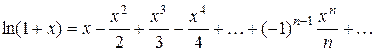

можем записать

.

Отсюда получаем

Раскрывая скобки и приводя подобные члены, находим искомое разложение:

.

Очевидно, ряд сходится в интервале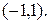

9. Разложить в ряд Маклорена функцию

Решение. Имеем Воспользовавшись разложением

,

нетрудно получить разложение

,

справедливое для интервала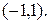

10. Найдите сумму ряда .

Решение. Рассмотрим ряд 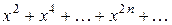, исследуем его на сходимость:

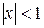, при - ряд сходится (при - расходится). Сумма этого ряда , так как ряд представляет собой геометрическую прогрессию. Таким образом, . Проинтегрируем обе части полученного разложения:

,

,

.

11. Найдите сумму ряда .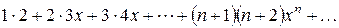

Решение. Воспользуемся бесконечной геометрической прогрессией

(сходится при ).

Дважды продифференцируем ряд:

,

.

Дата добавления: 2015-07-25