Методические рекомендации. Практическое занятие № 39

Практическое занятие № 39

Тема занятия « Числовые ряды. Ряды с положительными членами и признаки их сходимости: признаки сравнения, Даламбера, Коши »

Цель занятия: Формирование умений исследовать знакоположительные ряды на сходимость.

Организационная форма занятия: практикум с применением интерактивной доски.

Компетенции, формируемые на занятии:

- способность и готовность анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических, и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1).

Формирование у будущих специалистов этой компетенции предполагает обучение студентов

- сформулировать гипотезу и проверить ее в дальнейшем;

- анализировать ситуации и делать выводы;

- ставить новые вопросы и видеть проблемы в традиционных ситуациях;

- абстрагировать содержание и выделять существенное.

Вопросы, выносимые на обсуждение

1. Определение числового ряда, суммы ряда.

2. Необходимый признак сходимости числового ряда.

3. Признаки сравнения для сходимости знакоположительных рядов.

4. Признак Даламбера сходимости знакоположительных рядов.

Методические рекомендации

Для подготовки к занятию дома

1. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.

2. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.

3. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.

4. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.

5. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.

На занятии по указанию преподавателя

1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.

2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.

3. Разберите с преподавателем вопросы, которые остались Вами не понятыми по теме этого занятия.

Дома закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.

Рекомендуемая литература

[1] глава 10 пп 10.1.

[2] часть 2, глава III §1.

[3] глава 5 §§ 21– 22.

[6] глава 14 §§ 1 - 2.

[7] глава XIV §§ 1 - 2.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

1. Исследуйте ряд на сходимость .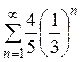

Решение. Ряд представляет собой бесконечно убывающую геометрическую прогрессию и поэтому является сходящимся. Согласно свойств числовых рядов данный ряд будет также сходящимся, так как если сходится ряд , то сходится и ряд , где С - некоторое число.

2. Определите сходится или расходится ряд .

Решение. Проверим необходимое условие сходимости числового ряда. Находим предел n -го члена ряда

следовательно, данный ряд расходится.

3. Примените признак сравнения для исследования сходимости ряда , если p < 1.

Решение. Так как для любых n > 1 и гармонический ряд 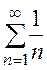расходится, то, по первому признаку сравнения числовых рядов, данный ряд является расходящимся.

4. Примените признак сравнения для исследования сходимости рядов

а) ; б) .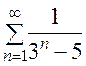

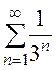Решение. а)Так как для любого n и ряд сходящийся, как бесконечно убывающая геометрическая прогрессия, то данный ряд сходится по первому признаку сравнения числовых рядов.

б) Сравним данный ряд вновь с рядом . В отличие от предыдущего примера для всех n, поэтому первый признак сравнения ответа не даст.

Воспользуемся вторым признаком сравнения числовых рядов. Для рядов и находим . Если этот предел есть конечное число, отличное от нуля, то ряды сходятся и расходятся одновременно.

Находим .

Следовательно, данный ряд сходится.

5. Примените признак Даламбера для исследования ряда .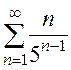

Решение. Выпишем n -й член ряда , тогда 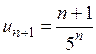. Воспользуемся признаком Даламбера.

Вычисляем . Так как D < 1, то данный ряд сходится.

---

Дата добавления: 2015-07-25