
Читайте также:
|
Для синтеза схемы любого автомата необходимо составить словесную формулировку условий его работы. Для синтеза схемы автомата Мили словесная формулировка должна включать в себя перечень всех возможных входных воздействий U и перечень соответствующих им выходных воздействий V, т.е. заказчиком должна быть составлена таблица соответствия входных воздействий и выходных воздействий. Индекс каждой буквы входа U и выхода V, соответствует двоичному числу входа и выхода. Пусть будет задана следующая таблица соответствия:
 .
.
 |
Рис. 5.1. Структурная схема автомата
Отсюда входные и выходные воздействия автомата в двоичном коде будут следующие


Синтез схем конечных автоматов делится на два этапа:
- абстрактный синтез,
- структурный синтез.
Основной задачей абстрактного синтеза является составление таблиц переходов и выходов, а также получение минимального числа элементов памяти.
В процессе структурного синтеза производится кодирование двоичными числами входов, выходов и внутренних состояний, получаются уравнения выходов, уравнения возбуждения элементов памяти и строится электрическая схема автомата.
5.1.1. Абстрактный синтез конечного автомата Мили
Пусть задана следующая таблица соответствия:
| Входы: | U 0 | U 1 | U 3 | U 7 | U 6 | U 2 | U 0 | U 4 | U 3 | U 1 | U 5 | U 2 | U 3 | U 7 | U 6 | U 4 | U 0 |
| Выходы: | V 0 | V 2 | V 3 | V 2 | V 3 | V 1 | V 3 | V 2 | V 1 | V 3 | V 2 | V 3 | V 3 | V 1 | V 1 | V 3 | V 0 |
Известно, что в конечном автомате Мили каждый выход формируется не только входным воздействием, но и внутренним состоянием. Поэтому в таблице соответствия каждому переходу необходимо присвоить внутреннее состояние, которое обозначим буквой а. Таблица соответствия будет следующая:
| Входы: | U 0 | U 1 | U 3 | U 7 | U 6 | U 2 | U 0 | U 4 | U 3 | U 1 | U 5 | U 2 | U 3 | U 7 | U 6 | U 4 | U 0 |
| Внутреннее состояние: | а 0 | а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 | а 8 | а 9 | а 10 | а 11 | а 12 | а 13 | а 14 | а 15 | а 16 |
| Выходы: | V 0 | V 2 | V 3 | V 2 | V 3 | V 1 | V 3 | V 2 | V 1 | V 3 | V 2 | V 3 | V 3 | V 1 | V 1 | V 3 | V 0 |
Совмещенная таблица переходов и выходов составляется следующим образом (см. таблицу 5.1). В верхнюю строку заносятся все внутренние состояния  . Число следующих строк будет равно числу различных входных воздействий
. Число следующих строк будет равно числу различных входных воздействий  , число столбцов таблицы равно числу внутренних состояний.
, число столбцов таблицы равно числу внутренних состояний.
Заполняются клетки совмещенной таблицы переходов и выходов следующим образом. Руководствуясь таблицей соответствия с присвоенными внутренними состояниями, в клетки таблицы записываются внутренние состояния и соответствующие им выходы. Данные из таблицы соответствия заносятся слева направо в порядке очередности. Начинается таблица соответствия с входного воздействия U 0, внутреннего состояния а 0 и выходного сигнала V 0. В клетку на пересечении строки U 0 и столбца а 0 заносятся в виде дроби  (внутреннее состояние а 0 в числителе, выходной сигнал V 0 в знаменателе). Данная заполненная клетка таблицы переходов и выходов является исходным состоянием автомата, следующее входное воздействие U 1 переводит его в состояние а 1 из состояния а 0, поэтому в клетку не пересечении столбца а 0 и строки U 1 записывается дробь
(внутреннее состояние а 0 в числителе, выходной сигнал V 0 в знаменателе). Данная заполненная клетка таблицы переходов и выходов является исходным состоянием автомата, следующее входное воздействие U 1 переводит его в состояние а 1 из состояния а 0, поэтому в клетку не пересечении столбца а 0 и строки U 1 записывается дробь  и повторяется в этой строке на пересечении со столбцом а 1. Повторение записи необходимо для того, чтобы автомат остановился в состоянии а 1 и ожидал поступления очередного входного воздействия. Последующие переходы автомата выполняются аналогично.
и повторяется в этой строке на пересечении со столбцом а 1. Повторение записи необходимо для того, чтобы автомат остановился в состоянии а 1 и ожидал поступления очередного входного воздействия. Последующие переходы автомата выполняются аналогично.
Таблица 5.1.
Совмещенная таблица переходов и выходов
| а 0 | а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 | а 8 | а 9 | а 10 | а 11 | а 12 | а 13 | а 14 | а 15 | а 16 | |
| U 0 | 
| 
| 
| 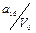
| 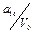
| ||||||||||||
| U 1 | 
| 
| 
| 
| |||||||||||||
| U 2 | 
| 
| 
| 
| |||||||||||||
| U 3 | 
| 
| 
| 
| 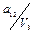
| 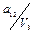
| |||||||||||
| U 4 | 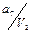
| 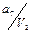
| 
| 
| |||||||||||||
| U 5 | 
| 
| |||||||||||||||
| U 6 | 
| 
| 
| 
| |||||||||||||
| U 7 | 
| 
| 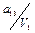
| 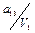
|
Полученная таблица переходов и выходов позволяет построить схему автомата Мили, который будет работать согласно заданной таблицы соответствия. Основным недостатком этого автомата является наличие в нем семнадцати внутренних состояний. Для того, чтобы создать семнадцать внутренних состояний необходимо в схеме автомата иметь пять элементов памяти, т.к. число внутренних состояний всегда равно 2n, где n – число элементов памяти.
Для сокращения числа элементов памяти в автомате необходимо выполнять минимизацию числа внутренних состояний в таблице 5.1.
Минимизация таблицы переходов и выходов сводится к сокращению числа столбцов путем наложения их друг на друга. Для этого существует два условия: необходимое и достаточное.
Необходимое условие заключается в том, что два столбца могут накладываться друг на друга, если клетки каждой строки будут или пустые, или одна заполнена, а другая пустая, или если обе заполнены, но имеют одинаковые выходные сигналы. Согласно этого условия друг на друга могут накладываться несколько столбцов. Единого варианта объединения столбцов не существует. Важно сократить число столбцов таблицы до минимума и чтобы при этом выполнялись необходимое и достаточное условие.
Достаточное условие заключается в том, чтобы в объединяемых клетках, если они обе заполнены были одинаковые внутренние состояния после их переобозначения.
По необходимому условию произведем объединение столбцов таблицы, переобозначив их буквой в:

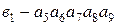

Таким образом, число внутренних состояний проектируемого автомата по необходимому условию сократилось с 17-ти до 3-х. Для того чтобы проверить выполнение достаточного условия надо построить таблицу аналогичную первой, только внутренние состояния в ней обозначить буквами в 0, в 1, в 2.
Из таблицы 5.2. следует, что все столбцы, намеченные к объединению по необходимому условию, объединяются и по достаточному условию, т.к. все заполненные клетки, которые объединяются между собой, заполнены одинаковыми внутренними состояниями. В результате объединения столбцов получим минимальную таблицу переходов и выходов (табл. 5.3).
Таблица 5.2.
Таблица переходов и выходов с переобозначенными
внутренними состояниями
| в 0 | в 0 | в 0 | в 0 | в 0 | в 1 | в 1 | в 1 | в 1 | в 1 | в 2 | в 2 | в 2 | в 2 | в 2 | в 0 | в 0 | |
| а 0 | а 1 | а 2 | а 3 | а 4 | а 5 | а 6 | а 7 | а 8 | а 9 | а 10 | а 11 | а 12 | а 13 | а 14 | а 15 | а 16 | |
| U 0 | 
| 
| 
| 
| 
| ||||||||||||
| U 1 | 
| 
| 
| 
| |||||||||||||
| U 2 | 
| 
| 
| 
| |||||||||||||
| U 3 | 
| 
| 
| 
| 
| 
| |||||||||||
| U 4 | 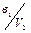
| 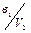
| 
| 
| |||||||||||||
| U 5 | 
| 
| |||||||||||||||
| U 6 | 
| 
| 
| 
| |||||||||||||
| U 7 | 
| 
| 
| 
|
Если бы какая-либо группа столбцов, намеченная к объединению по необходимому условию, по достаточному условию не объединилась, то необходимо выполнить новое переобозначение столбцов для их объединения по необходимому условию и вновь проверить выполнение достаточного условия. Таким образом, объединять столбцы можно только после выполнения обоих условий.
Таблица 1.3
Минимальная таблица переходов и выходов
| в 0 | в 1 | в 2 | |
| U 0 | 
| 
| |
| U 1 | 
| 
| |
| U 2 | 
| 
| 
|
| U 3 | 
| 
| 
|
| U 4 | 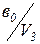
| 
| 
|
| U 5 | 
| 
| |
| U 6 | 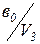
| 
| |
| U 7 | 
| 
|
5.1.2. Структурный синтез конечного автомата Мили
Кодирование входов и выходов осуществляется путем перевода индексов входных воздействий U и выходных сигналов V в двоичные числа. В результате получим:



Для кодирования внутренних состояний необходимо по полученной минимальной таблице переходов и выходов 5.3. построить граф автомата. Граф состоит из вершин (кружков) и ребер (линий), которыми соединяются вершины между собой. Вершины представляют собой все внутренние состояния автомата, а ребра переходы автомата из одного состояния в другое при подаче входных воздействий. Каждое ребро на графе обозначается входом и через дробь соответствующим ему выходом. Если под воздействием какого-либо входа автомат не меняет своего внутреннего состояния, то данное ребро проводится в виде полукольца около данной вершины.
На основе минимальной таблицы переходов и выходов получается граф автомата (рис. 5.2.).
В графе различают вершины смежные 1-го ранга, вершины смежные 2-го ранга и т.д. Вершинами смежными 1-го ранга являются те вершины, переход автомата, в которые происходит из другой вершины только с помощью одного ребра. Например, из вершины в 0 в вершину в 1 с помощью ребра  или с вершины в 2 в вершину в 0 с помощью ребра
или с вершины в 2 в вершину в 0 с помощью ребра  .
.



Рис. 5.2. Граф автомата
В графе все вершины смежные 1-го ранга должны кодироваться соседними двоичными числами, которые отличаются между собой только в одном разряде. Количество разрядов двоичных чисел, которыми кодируются вершины графа, зависит от количества вершин в графе, т.е. от количества внутренних состояний автомата. Следовательно, каждый разряд двоичного числа, которым закодирована вершина графа, соответствует одному элементу памяти. Если все смежные вершины 1-го ранга в графе автомата закодированы соседними двоичными числами, то переход автомата из одного состояния в другое при подаче одного входного воздействия U будет происходить за счет изменения состояния только одного элемента памяти. В этом случае сбоев в работе автомата не будет. В случае, если смежные первого ранга (внутренние состояния) будут закодированы не соседними двоичными числами (например в 1 – 01, в 2 – 10), то при переходе автомата из состояния в 1в состояние в 2 необходимо изменить состояние обоих элементов памяти. Так как совершенно одинакового быстродействия элементов автоматики не бывает, то автомат из состояния 01 (6) может перейти или в состояние 00, или в состояние 11, а, следовательно, будет появляться ложный выходной сигнал. Это и будет являться сбоем в работе автомата.

в 0 в 1
в 3 в 2
Рис. 5.3. Граф автомата с четным числом вершин
После построения графа автомата определяется возможность кодирования вершин графа смежных первого ранга соседними двоичными числами. Одним из условий такой возможности является четное число вершин во всех замкнутых контурах графа. Если имеют место контуры с нечетным числом вершин, то необходимо в эти контуры добавить вершину, которая будет соответствовать неустойчивому внутреннему состоянию автомата. В рассматриваемом автомате граф (рис. 5.2) состоит из контура с тремя вершинами, которые закодировать соседними двоичными числами не представляется возможным, поэтому в граф вводим дополнительную вершину в 3 (рис. 5.3).
Вершина в 3будет неустойчивой, т.е. автомат из вершины в 2 под воздействием ребра  сигнала перейдет в состояние в 3 и, не останавливаясь в этом состоянии, перейдет в состояние в 0.
сигнала перейдет в состояние в 3 и, не останавливаясь в этом состоянии, перейдет в состояние в 0.
Так как в граф введена дополнительная вершина в 3, то минимальная, абстрактная таблица будет иметь вид (табл. 5.4), где добавлен столбец, соответствующий в 3 и показано, что по сигналу U 4 автомат переходит из состояния в 2 в неустойчивое состояние в 3, а затем в состояние в 0 без изменения входного сигнала.
Таблица 5.4.
Минимальная абстрактная таблица
| в 0 | в 1 | в 2 | в 3 | |
| U 0 | 
| 
| ||
| U 1 | 
| 
| ||
| U 2 | 
| 
| 
| |
| U 3 | 
| 
| 
| |
| U 4 | 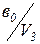
| 
| 
| 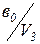
|
| U 5 | 
| 
| ||
| U 6 | 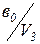
| 
| ||
| U 7 | 
| 
|
Кодирование вершин соседними двоичными числами показано на графе (рис. 5.2).
Выполнив кодирование входов, выходов и внутренних состояний автомата двоичными числами на основе совмещенной минимальной абстрактной таблицы 5.4. построим отдельно структурную таблицу переходов и структурную таблицу выходов путем замены букв входов U, выходов V, внутренних состояний в их двоичными кодами.
Таблица 5.5.
Структурная таблица переходов
Таблица 5.6.
Структурная таблица выходов
Получение уравнений выходов
Известно, что количество разрядов двоичных чисел, которыми кодируются входы равно количеству входов автомата, соответственно внутренние состояния – количеству элементов памяти, выходы – количеству выходов автомата. В рассматриваемом примере количество входов три Х 1 Х 2 Х 3, элементов памяти два Q 1 Q 2, выходов два Y 1 Y 2 (см. таблицу 5.5). Отсюда следует, что выходы Y 1 и Y 2 будут зависеть от пяти переменных X 1 X 2 X 3 q 1 q 2, т.к. выходы автоматов Мили формируются входными воздействиями и внутренними состояниями. Уравнения выходов Y 1 Y 2из структурной таблицы выходов можно получить двумя способами:
7. Сначала получить уравнения в виде СДНФ, а потом их минимизировать.
8. Сразу получить минимальные уравнения, используя матрицу на пять переменных.
Получим сразу минимальные уравнения выходов. Для этого необходимо в структурной таблице выходов произвести перестановку строк таким образом, чтобы все рядом расположенные строки имели соседние двоичные числа кодов входных воздействий. Преобразованная таблица выходов имеет следующий вид:
Таблица 5.7.
Преобразованная таблица выходов
Уравнения выходов Y 1 и Y 2 получаем с помощью матриц на пять переменных, которые строятся на основе таблицы 5.7.
Для получения уравнения выхода Y 1 строим матрицу на пять переменных. В клетки матрицы заносим значение Y 1из таблицы 5.7.
Объединив клетки, в которых Y 1равен 1, в контуры получим уравнение выхода Y 1:

Аналогично строим матрицу на пять переменных для Y 2 и получим уравнение выхода Y 2.
 Таблица 5.8.
Таблица 5.8.
Матрица на пять переменных для выхода Y 1
| q 1 q2 Х 1 Х 2 Х 3 | ||||
| (1) | (1) | |||
| (1) | (1) | |||
| (1) | ||||
| (1) | ||||
| (1) | ||||
| (1) | ||||
| (1) | (1) | |||
| (1) |
Таблица 5.9.
Матрица на пять переменных для выхода Y 2
 q 1 q 2
X 1 X 2 X 3 q 1 q 2
X 1 X 2 X 3
| ||||
| (1) | (1) | |||
| (1) | (1) | |||
| (1) | ||||
| (1) | ||||
| (1) | (1) | |||
| (1) | ||||

Получение уравнений возбуждения элементов памяти Q 1 и Q 2
Для получения уравнений возбуждения элементов памяти необходимо структурную таблицу переходов преобразовать в таблицу возбуждения элементов памяти.
Если в клетках структурной таблицы переходов стоят состояния элементов памяти, то в клетках таблицы возбуждения должны находиться состояния входов элементов памяти. Поэтому прежде, чем строить таблицу возбуждения, необходимо выбрать элементы автоматики и телемеханики, которые будут использоваться в качестве элементов памяти. Элементами памяти могут быть нейтральные реле или триггеры. Для выбранного элемента памяти строится таблица его переходов, на основе которой делается вывод о зависимости состояния входа элемента памяти от состояния самого элемента памяти. После этого в клетках таблицы переходов проектируемого автомата, состояния элементов памяти заменяются состояниями входов этих элементов памяти.
Рассмотрим применение в проектируемом автомате в качестве элементов памяти реле и триггеров с одним входом.
Построение таблицы возбуждения
Если в качестве элемента памяти используется реле, то его таблица переходов будет следующая.
Таблица 5.10.
Таблица переходов реле
Столбцы таблицы обозначаются устойчивыми состояниями самого реле. У реле два устойчивых состояния: якорь отпущен «0» и якорь притянут к сердечнику «1». Строки таблицы обозначены состояниями входа реле: нет тока в катушке «0», подается ток в катушку «1». В клетках таблицы находятся состояния реле, в которые оно переходит под воздействием входов. Из таблицы следует, что если на вход реле подается «0», то оно всегда перейдет в состояние «0» как из начального состояния «0», так и из состояния «1». Если на вход реле подается «1», то реле всегда переходит в состояние «1». Таким образом, для реле его состояния всегда повторяют состояния входов. Отсюда можно сделать вывод о том, что таблица переходов автомата одновременно будет являться и таблицей возбуждения, т.к. состояния элементов памяти, находящиеся в клетках, будут и состояниями входов.
На основе таблицы возбуждения построим две матрицы на пять переменных и получим уравнения возбуждения элементов памяти Q 1 и Q 2 аналогично тому, как это делалось при получении уравнений выходов.
Таблица 5.11.
Матрица на пять переменных для Q 1
 001 001
| ||||
| (1) | (1) | |||
Таблица 5.12.
Матрица на пять переменных для Q 2
 000 000
| ||||
| (1) | ||||
| (1) | ||||
| (1) | (1) | |||
| (1) | (1) | |||
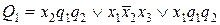
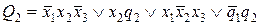
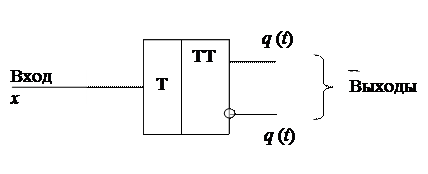 Рассмотрим построение таблицы возбуждения и получение уравнений возбуждения элементов памяти, если в качестве элементов памяти будут использоваться Т-триггеры, имеющие один информационный вход.
Рассмотрим построение таблицы возбуждения и получение уравнений возбуждения элементов памяти, если в качестве элементов памяти будут использоваться Т-триггеры, имеющие один информационный вход.
 |
Рис. 5.4. Триггер с одним входом
Триггер имеет два устойчивых внутренних состояния, которые обозначаются 0 и 1. На вход триггера могут, подаваться двоичные сигналы 0, не изменяющий состояние триггера, и 1, переводящий триггер в противоположное состояние. У триггера есть два выхода: прямой q (t) и инверсный  . Сигнал q (t) на прямом выходе соответствует внутреннему состоянию триггера 0. При переходе триггера в состояние 1 сигналы на выходах меняют местами. Функционирование триггера осуществляется в соответствии с таблицей 5.13.
. Сигнал q (t) на прямом выходе соответствует внутреннему состоянию триггера 0. При переходе триггера в состояние 1 сигналы на выходах меняют местами. Функционирование триггера осуществляется в соответствии с таблицей 5.13.
Таблица 5.13.
Таблица переходов Т-триггера
| q (t) | ||
| Состояние Вход | ||
Из таблицы переходов следует, что входной сигнал Т-триггера всегда будет равен сумме по модулю 2 внутренних состояний триггера, в котором он был (одна из клеток верхней строки) и в которое переходит под воздействием этого входного сигнала (соответствующая клетка таблицы).
Согласно установленной зависимости входного сигнала из таблицы переходов автомата 5.5 получаем таблицу возбуждения автомата путем суммирования состояний элементов памяти, находящихся в клетках таблицы, с состояниями элементов памяти, которыми обозначены столбцы таблицы.
Таблица 5.14.
Таблица возбуждения автомата
На основе полученной таблицы возбуждения автомата строим матрицы на пять переменных для каждого элемента памяти, и получаем уравнения возбуждения элементов памяти (триггеров с одним входом).
Таблица 5.15.
Матрица для Q 1
 000 000
| (1) | |||
| (1) | ||||
| (1) | ||||
| (1) | ||||
| (1) | ||||
| (1) | ||||
| (1) | (1) | |||

Таблица 5.16.
 Матрица для Q 2
Матрица для Q 2
| (1) | ||||
| (1) | ||||

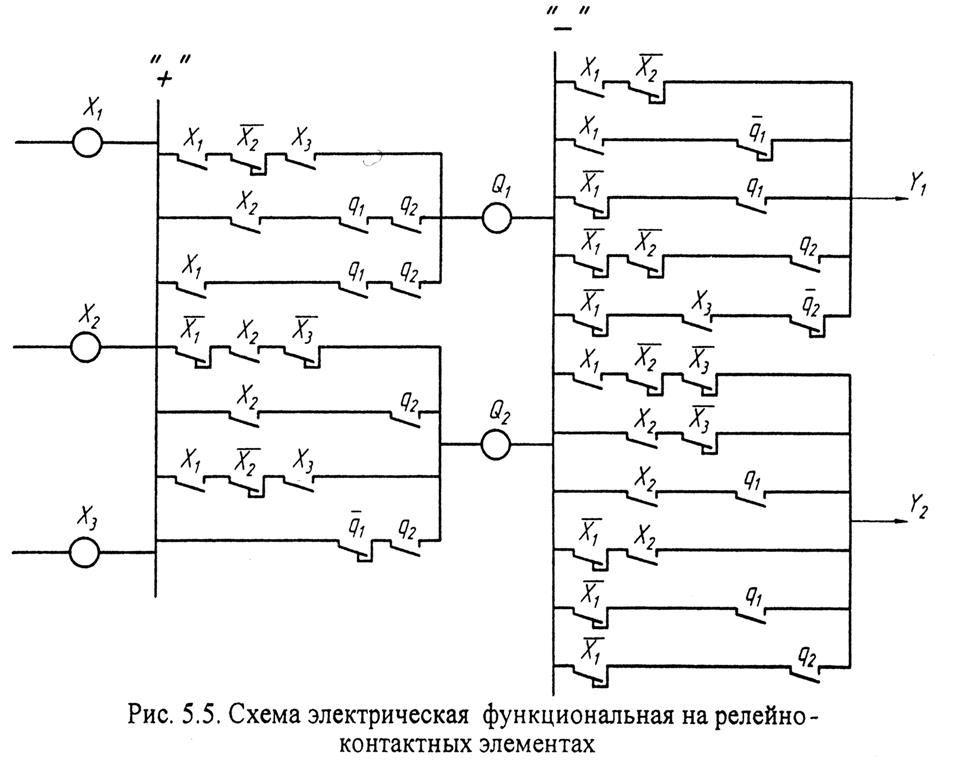
5.1.3. Построение схем электрических функциональных автомата Мили
Схема электрическая функциональная на релейно-контактных элементах строится на основе уравнений возбуждения Q 1 и Q 2 и уравнений выходов Y 1 Y 2


Схема представлена на рис. 5.4.
Для построения электрической схемы на логических элементах необходимо решить две задачи:
1. Выбрать базис логических элементов.
2. Выбрать элемент автоматики, который будет использоваться в качестве элемента памяти (триггер с одним входом или триггер с двумя входами).
В данной случае три базиса логических элементов:
1. «И», «ИЛИ», «НЕ».
2. «И-НЕ».
3. «ИЛИ-НЕ».
В качестве элемента памяти используем только триггер с одним входом. Функциональная схема автомата на логических элементах базиса «И», «ИЛИ», «НЕ» строится согласно уравнений возбуждения элементов памяти 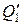 ,
,  и уравнений выходов Y 1 Y 2. Схема представлена на рис. 5.5.
и уравнений выходов Y 1 Y 2. Схема представлена на рис. 5.5.
Для построения функциональных электрических схем на логических элементах базисов «И-НЕ» и «ИЛИ-НЕ» необходимо уравнения  ,
,  , Y 1и Y 2привести к этим базисам. Для этого используются два закона алгебры логики:
, Y 1и Y 2привести к этим базисам. Для этого используются два закона алгебры логики:
- закон двойного отрицания,
- закон инверсии.
Если выбирается базис «И-НЕ», то уравнения возбуждения элементов памяти  ,
,  и уравнения выходов Y 1 Y2 будут следующими:
и уравнения выходов Y 1 Y2 будут следующими:

Из полученных уравнений следует, что применение двух законов алгебры логики позволяет в уравнениях избавиться от операции логического сложения, т.е. в уравнениях остаются только операции логического умножения и отрицания, что соответствует базису «И-НЕ».
Схема электрическая функциональная, построенная на логических элементах «И-НЕ» представлена на рисунке 5.6.
Для базиса «ИЛИ-НЕ» уравнения будут иметь вид:

Схема электрическая функциональная на логических элементах «ИЛИ-НЕ» представлена на рис. 5.7.



Если в качестве элемента памяти будет использоваться триггер с двумя входами (IK-триггер или RS-триггер), то для построения таблицы возбуждения необходимо использовать таблицу переходов одного из указанных триггеров. Например, для IK-триггера таблица переходов будет следующая
Таблица 5.16.
Таблица переходов IK-триггера
| IK | ||
| – | – |
Из таблицы 5.16 следует, что единичный сигнал на входе I переводит триггер в состояние 1, а единичный сигнал на входе К в состояние 0. Таким образом, получается система подстановок состояний триггера и состояний его входов
 . (5.1)
. (5.1)
В скобках с дробью показаны переходы состояний триггера из ноля (числитель) в ноль (знаменатель), из ноля в единицу, из единицы в ноль и из единицы в единицу, а в скобках без дроби состояния входов триггера. Прочерк вместо одного из входов означает, что данный вход может быть равен или нулю, или единице (важно значение другого входа).
Таблица возбуждения синтезируемого конечного автомата Мили с учетом структурной таблицы переходов 5.5 и системы подстановок представлена таблицей 5.16.
Таблица 5.16.
Таблица возбуждения при использовании в качестве
элемента памяти IK-триггера
| Q 1 Q 2 | ||||
| х 1 х 2 х 3 | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 0 | 0 – 0 – | 0 – – 0 | ||
| 0 0 1 | 0 – 0 – | 0 – – 0 | ||
| 0 1 0 | 0 – 1 0 | 0 – – 0 | – 0 – 0 | |
| 0 1 1 | 0 – 0 – | 0 – – 0 | – 0 – 0 | |
| 1 0 0 | 0 – 0 – | 0 – – 0 | – 0 0 1 | 0 1 0 – |
| 1 0 1 | 1 0 – 0 | – 0 – 0 | ||
| 1 1 0 | 0 – 0 – | – 0 – 0 | ||
| 1 1 1 | 0 – 0 – | – 0 – 0 |
Ранее было отмечено, что таблица переходов 5.5 содержит два элемента памяти Q 1, Q 2. В таблице возбуждения 5.16 столбцы обозначены так же, как и в таблице переходов 5.5 внутренними состояниями элементов памяти, а клетки таблицы на основе системы подстановок заполняются состояниями входов триггеров. При этом числитель скобки с дробью стоит в верхней строке таблицы переходов, а знаменатель в соответствующей клетке таблицы. В этой клетке таблицы возбуждения вместо внутреннего состояния триггера ставится состояние входов триггера на основе системы подстановок. Из таблицы возбуждения 5.16 необходимо получить уравнения возбуждения для четырех входов двух элементов памяти IK-триггеров Q 1 I, Q 1 K, Q 2 I и Q 2 K.
Для этого необходимо построить четыре матрицы минимизации на пять переменных.
Таблица 5.17.
Матрица для входа Q 1 I
 0 0
| ||||
| (1) | (1) | (1) | ||
 .
.
Таблица 5.18.
 Матрица для входа Q 1 К
Матрица для входа Q 1 К
 .
.
Таблица 5.19.
Матрица для входа Q 2 I
 0 0
| ||||
 .
.
Таблица 5.20.
 Матрица для входа Q 2 К
Матрица для входа Q 2 К
| (1) | (1) | |||
| (1) |
 .
.
Получив уравнения возбуждения элементов памяти (триггеров с двумя входами), построим электрическую функциональную схему на логических элементах базиса «И», «ИЛИ», «НЕ».

Рис. 5.8. Схема электрическая функциональная возбуждения элементов
памяти автомата Мили на логических элементах
базиса «И», «ИЛИ», «НЕ»
Контрольные вопросы
1. Задачи абстрактного синтеза конечных автоматов?
2. Задачи структурного синтеза конечных автоматов?
3. В чем заключается минимизация таблицы переходов и выходов автомата?
4. Дать определение необходимого и достаточного условия для объединения столбцов таблицы переходов и выходов синтезируемого автомата.
5. Как кодируются входные, выходные воздействия и внутренние состояния автомата?
6. Для чего необходимо вершины смежные первого ранга в графе автомата кодировать соседними двоичными числами?
7. Для чего строится таблица возбуждения автомата, и чем она отличается от таблицы переходов?
8. Пояснить таблицу переходов реле.
9. Пояснить таблицы переходов триггеров с одним и двумя входами.
10. Чем отличаются конечные автоматы от комбинационных автоматов?
11. Чем отличаются конечные автоматы Мили от конечных автоматов Мура?
12. Дать определение необходимого и достаточного условий для минимизации отмеченной таблицы переходов автомата Мура.
Дата добавления: 2015-07-25; просмотров: 116 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СИНТЕЗ КОМБИНАЦИОННЫХ АВТОМАТОВ | | | СИНТЕЗ КОНЕЧНЫХ АВТОМАТОВ МУРА |