Лабораторна робота № 4

ОСОБЛИВОСТІ МОДЕЛЮВАННЯ ТВЕРДОТІЛЬНИХ ЛАЗЕРІВ ЗІ СКЛАДНОЮ СИСТЕМОЮ ЕНЕРГЕТИЧНИХ РІВНЕЙ

Мета роботи: засвоїти навички моделювання твердотільних лазерів зі складною системою енергетичних рівнів.

ТЕОРЕТИЧНІ ВІДОМОСТІ

Для деяких твердотільних активних середовищ наближення дворівневої моделі може виявитися недостатнім при проведенні досліджень деяких типів лазерів. Так, наприклад, неможливо оцінити вплив кінцівки часу життя нижнього лазерного рівня на процеси генерації. Вивчення процесів кросу-релаксації в активних середовищах, поглинання зі збуджених станів під дією випромінювання накачки також не можуть бути досліджені в рамках дворівневого наближення. У цьому розділі буде показано, як можна провести дослідження процесів генерації в рамках точкової моделі твердотільного лазера, але з великою кількістю енергетичних рівнів, залучених в схему генерації. Прототипом такої моделі можуть служити кристалічні лазери на базі середовищ, активованих іонами ербію, при розгляді генерації випромінювання на переході ⁴I_11/2 – ⁴I_13/2. Особливістю даного переходу є відносно великий час життя нижнього лазерного рівня ⁴I_13/2 - (8-10)мс для всіх матриць. Часи життя верхнього лазерного рівня ⁴I_11/2 для більшості кристалічних матриць також мають значення в діапазоні мілісекунди (YLF:Er - 4мс, YSGG:Er - 2мс). Виняток складає досить поширена і широко вживане на практиці активне середовище на основі ітрій алюмінієвого граната YAG:Er, для якого час життя рівня ⁴I_11/2 складає всього 0,1мс.

На рис.1 приведена спрощена схема енергетичних рівнів іонів ербію Er³⁺ в кристалі YLF (YLiF₄). Окрім основного ⁴I_15/2, нижнього ⁴I_13/2 і верхнього ⁴I_11/2 лазерних рівней на рис.3 зображені ще два вищерозміщені енергетичні рівні: ⁴I_9/2 і самий верхній енергетичний рівень, в який умовно об'єднані вищерозміщені енергетичні рівні іонів ербію: ⁴F_9/2, ⁴S_3/2, ²Н_11/2, ⁴F_7/2. Таким чином, в даному випадку застосовується п'ятирівнева фізична модель іонів ербію в матриці YLF.

На рис.1 прямі лінії, з’єднані пунктиром, позначають найбільш важливі крос-релаксаційні переходи в іонах ербію. Під крос-релаксаційними переходами розуміють взаємодію між двома іонами ербію, що знаходяться в різних або в одному і тому ж збуджених станах. В результаті взаємодії енергетичні стани іонів міняються, причому енергія одного іона збільшується, а іншого іона зменшується. Даний процес відноситься до процесів апконверсії, тобто процесам, при яких відбувається заселення верхніх рівнів іонів ербію. Спостерігаються і релаксаційні процеси іншого типу, при яких релаксація іона з вищерозміщеного рівня вниз (наприклад, ⁴IS_3/2 → ⁴I_9/2) супроводжується одночасним збудженням іншого іона з основного стану ⁴I_15/2 на нижній лазерний рівень ⁴I_13/2. Такі переходи приводять до самотушення люмінесценції, оскільки кількість іонів ербію, що знаходяться на верхніх енергетичних рівнях і беруть участь в процесах люмінесценції з верхніх рівнів іонів ербію, зменшується. Відзначимо, що всі наведені вище процеси відбуваються практично без передачі або з мінімальною передачею енергії збуджених іонів ербію фононам кристалічної решітки.

Генерація в іонах ербію реалізується на переході між одним з шести штарковських підрівнів верхнього лазерного рівня ⁴I_11/2 і одним з семи підрівнів нижнього лазерного рівня ⁴I_13/2. Розщепленя мультіплетов і положення штарковських рівнів для іонів ербію Er³⁺ в YLiF₄ приведені в таблиці 1.

Таблиця 1

Положення штарковських підрівнів для мультіплетів ⁴I_11/2 і ⁴I_13/2 іона Er³+ в кристалі Er:YLF

Мультиплет	Положення штарковських рівнів, см^-1
^4I13/2	6540; 6545; 6585; 6680; 6704;6731;6745
^4I11/2	10213; 10230; 10290; 10300; 10309;10329

Довжина хвилі генерації 2.81 мкм відповідає переходам між 3, рахуючи знизу вверх, підрівнем верхнього лазерного рівня ⁴1_11/2 і 6 підрівнем нижнього лазерного рівня ⁴1_13/2. Теплова рівновага між підрівнями мультіплетов іонів ербію встановлюється дуже швидко, так що можна вважати, що розподіл іонів по підрівнях всередині мультиплета підкоряється закону Больцмана.

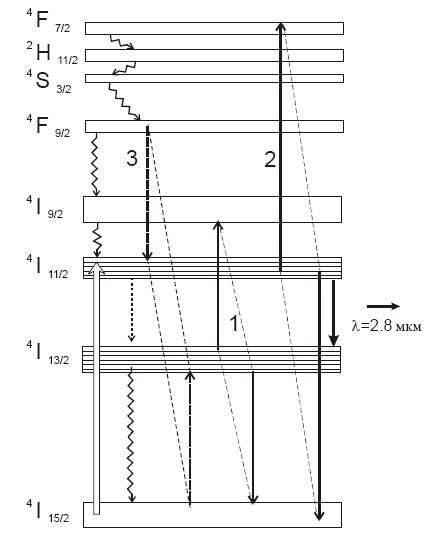
Рис.4.1 Спрощена схема енергетичних рівнів в лазерному кристалі YLiF₄, активованому іонами ербію. Прямими лініями, з’єднаними пунктиром, показані крос-релаксаційні переходи, 1 і 2 процеси апконверсиі, 3 - самотущення люмінесценції.

Приведемо систему швидкісних рівнянь, що описують в одномодовому наближенні, генерацію в YLF:Er лазері з урахуванням переходів між 5 нижніми рівнями. Додатково передбачається, що накачка іонів ербію здійснюється за допомогою лазерних діодів з довжиною хвилі генерації приблизно 0.98мкм.

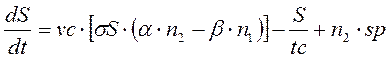
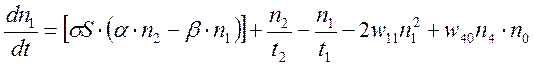
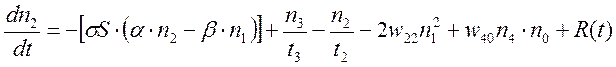
(4.1)

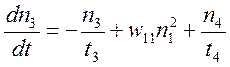
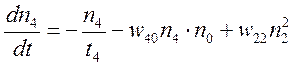
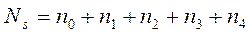
Позначення:

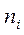- щільність населеності і-рівня;

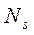- об'ємна щільність іонів ербію в кристалі;

S - щільність потоку випромінювання, що генерується, всередині резонатора;

vc - швидкість світла в середовищі;

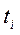- час життя і-рівня;

w₄₀ - швидкість безвипромінювальних крос-релаксаційних переходів з рівня 4 на рівень 2 і з основного рівня 0 на рівень 1.

w₁₁ і w₂₂ визначають вірогідності крос-релаксаційних процесов апконверсії на рівнях 1 і 2;

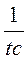- зворотний час життя фотона в резонатор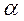і;

і 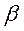визначають відносні населеності підрівнів мультіплетов ⁴1_11/2 і ⁴1_13/2;

R(t) - швидкість когерентної накачки верхнього лазерного рівня, яка може, в принципі, мінятися в перебігу імпульсу накачування.

Дана система рівнянь може бути розрахована із застосуванням математичних пакетів, наприклад, Mathcad 14. Приведемо скріншоти для програми, що дозволяє зробити моделювання характеристик YLF:Er лазера. Заздалегідь зробимо наступні зауваження по прийнятих нижче позначеннях. Шукані функції при рішенні мають стандартне позначення у вигляді масиву (матриці) <<х>>. Позначення <<х₀>> відноситься до функції S з системи рівнянь 4.1, тобто до щільності потоку випромінювання, що генерується, усередині резонатора. Розмірність величини S дорівнює [фотон/см² ∙с]. Функції <<x_i>>для і=1,2,3,4 представляють щільність населенностей відповідних рівнів 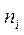з системи 4.1. Населеність основного нижнього рівня 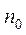знаходиться за допомогою нижнього рівняння з системи 4.1:

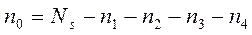(4.2)

Передбачається, що активне середовище має повну довжину Lar. Довжина прокачуваної області активного середовища має величину lar < Lar, величина показника заломлення активного середовища позначена як nar. Параметр µ характеризує міру заповнення резонатора активним середовищем. Величина µ розраховується по формулі:

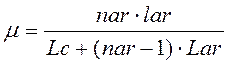(4.3)

Тут Lс геометрична довжина резонатора лазера. Величина, зворотна часу життя фотона в резонаторі 1/tc, що характеризує швидкість (вірогідність) втрат випромінювання в резонаторі лазера може бути знайдена з вираження:

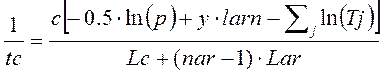(4.4)

В формулі (4.4) <<с>>- швидкість світла у вакуумі, 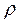- коефіцієнт віддзеркалення вихідного напівпрозорого дзеркала, 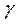- показник неактивних втрат випромінювання в активному середовищі в [см^-1], T_j коефіцієнти

пропускання випромінювання оптичними елементами, що встановлюються в резонаторі лазера.

Величина швидкості накачки R₀ рівня n₂ під дією випромінювання накачки для випадку подольної накачки визначається з рівняння:

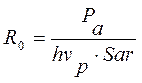(4.5)

де P_a - повна потужність випромінювання накачки, що поглинається в ефективному об'ємі Var=Sar∙lar активного середовища, Sar - площа поперечного розрізу активного середовища, hv_p- енергія кванта випромінювання накачки з довжиною хвилі λ_p = с/v_р. Нагадаємо, що, в загальному випадку нерівномірного по довжині активного середовища щільності випромінювання накачки, швидкість накачки робочого рівня в одиниці об'єму активного середовища на відстані << х>> від початкової плоскості введення випромінювання накачки в активне середовище, може бути представлена у вигляді:

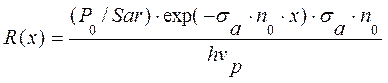(4.6)

Тут 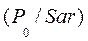- щільність потужності випромінювання накачки, падаючого на вхідну плоскість активного середовища.

Як учбове завдання, покажіть, що якщо довжина активного середовища при продольній накачці така, що все випромінювання поглинається всередині активного середовища, то формула (4.6) переходить у формулу (4.5).

Далі приведені скріншоти програми для розрахунку динаміки генерації YLF:Er лазера. Деякі додаткові роз'яснення по вибраній системі одиниць і позначенням параметрів проведені безпосередньо в тексті програми. Вживання позасистемних одиниць виміру дозволяє істотно зменшити розкидання діапазонів змін вживаних величин, що зменшує погрішність обчислень по програмах.

Введені вище функції tt, S, N1 - N4 є рішеннями системи рівнянь D(t,х) за допомогою оператора Rkadapt. Тривалість імпульсу випромінювання накачки складає в прикладі 900мкс, повна потужність накачки 500Вт. При записі початкових умов початковою тепловою заселеністю всіх рівнів нехтуємо. Початкова щільність потоку фотонів в резонаторі задається параметром s₀, вірогідність спонтанних переходів в одну генеруючу моду резонатора за допомогою параметра s_p. При заданні загальної кількості точок рішення NN множник 10 показує, що щільність вузлів рішення складає 10 точок на одну мкс. Природно, що всі параметри можуть бути легко змінені в процесі проведення модельних досліджень динаміки генерації YLF:Er лазера.

Функція U, яка дорівнює:

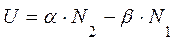(4.7)

представляє собою щільність інверсної населеності в активному середовищі між 3 і 6 робочими підрівнями рівнів ⁴I_11/2 и ⁴I_13/2 відповідно.

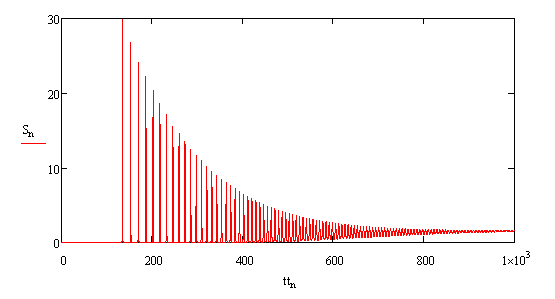На рис. 4.2а представлена ​​тимчасова залежність внутрірезонаторного потоку випромінювання геніраціі S. На рис. 4.2б зображені часові залежності для повних населенностей верхнього N2 і нижнього N1 рівнів іонів ербію, а також тимчасова залежність для щільності інверсної населеності U (t).

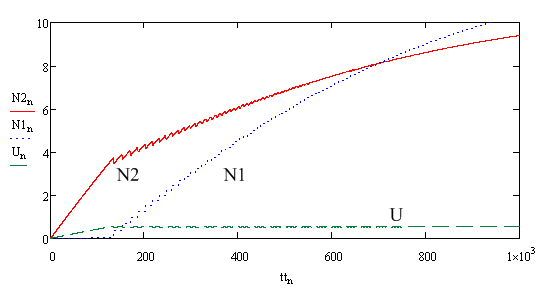
Рис. 4.2 Часові залежності

а) для внутрірезонаторного потоку випромінювання S,

б) щільностей повної заселеності верхнього N2 і нижнього N1 лазерних рівнів, а також щільності інверсної населеності U між підрівнями, які беруть участь у генерації.

З даних рис. (4.2) видно, що динаміка генерації для YLF:Er лазера має звичайний для більшості твердо тільних лазерів вигляд. Залежність щільності потоку S (t) має характерні релаксаційні коливання, поступово переходять у безперервний режим генерації випромінювання. Слід відзначити досить велике відношення амплітуди перших пучків генерації до стаціонарного значення. Залежність U (t) також має стандартний вигляд: зростання на першій часовій ділянці при відсутності генерації і стабілізацію середнього значення після початку генерації випромінювання.

Вищенаведене рішення передбачає накачування в верхній лазерний рівень N2. Населеність рівня N1 починає зростати тільки після початку генерації. Цікаво відзначити, що приблизно з 700мкс населеність нижнього лазерного рівня стає більше щільності населеності верхнього лазерного рівня N2 і різницею (N2-N1) продовжує зменшуватись з ростом часу. Це свідчить про те, що повний стаціонарний режим у лазера, який передбачає встановлення стаціонарних процесів в динаміці переходів між рівнями іонів ербію, в даному часовому періоді ще не наступив, хоча щільність потоку генерованого випромінювання стає практично незмінною. Проведення розрахунків при великій тривалості імпульсу випромінювання накачування показав, що стаціонарний режим для населенностей рівнів N2 i N1 настає при тривалості імпульсу накачки більше 2.3мс. 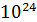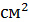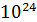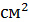Цікаво відзначити, що на тимчасовому відрізку від 1мс і далі відбувається поступове збільшення середньої величини внутрірезонаторної щільності потоку випромінювання від 1.6* 1/ с до стаціонарної величини 1.96* 1/ с.

Дослідження на представленій моделі лазера на основе YLF:Er дозволяють визначити вплив крос-релаксаційних констант на параметри режиму генерації і на встановлення стаціонарних значень для характеристик S і U. Деякі результати дослідження зведені в таблицю 1.

В таблиці 2 величина t_N відповідає часу встановлення стаціонарних значень для щільності населеності рівнів N₁ і N₂. Прочерки для значень S означають, що стаціонарний режим безперервної генерації випромінювання в лазері не встановлюється. Часи встановлення стаціонарних значень для рівнів N₁ і N₂ можуть істотно відрізнятися один від одного залежно від величин початкових значень параметрів моделі. Для таких умов час встановлення для рівня N₁ завжди виявляється більше, ніж час встановлення для рівня N₂, оскільки час життя нижнього лазерного рівня істотно більше часу життя верхнього лазерного рівня за відсутності крос-релаксаційних переходів.

Таблиця 2

Вплив крос-релаксаційних констант W₁₁, W₂₂ і W₄₀ на параметри генерації YLF:Er лазера

	Умовні значення крос-релаксаційних констант
W11∙1016^16,см^3/с
W22∙10^16,см^3/с
W40∙10^17,см^3/с
S∙10^-24,1/см^2с	-	3.9	-	-	-	3.3	1.93	1.96
tN, мс	>40	2.6	>40	>40	>40	2.5	2.3	2.3

З даних таблиці виходить:

- наявність крос-релаксаційного процесу з ненульовою вірогідністю W₁₁, що розселяє нижній лазерний рівень, необхідного для встановлення режиму генерації безперервного випромінювання,

- рівність крос-релаксаційної константи W₂₂=0 приводить до істотного збільшення енергетичних параметрів генерації,

- наявність крос-релаксаційного процесу з вірогідністю W₄₀, що приводить до гасіння люмінесценції з верхніх рівнів іонів ербію і одночасного збільшення заселенностей рівнів N₁ і N₂, приводить до незначного зростання параметра S від значення S~1.96 при W₄₀=10^-17 см³/с до значення S~2.28 при W₄₀=10^-13 см³/с. Цей результат можна пояснити тим, що при одночасному заселенні верхнього і ніжнего лазерних рівнів значення параметра інверсної населеності

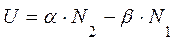збільшується, оскільки для даного генераційного переходу > .

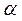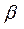Слід зазначити, що рамки справедливості наведених вище виводів залежать від конкретних співвідношень між прийнятими в моделі лазера константами крос-релаксаційних переходів. Експериментальне визначення крос-релаксаційних констант представляє істотні труднощі, тому точність їх завдання в даній моделі лазера відносно невелика.

Наявність апконверсійних крос-релаксаційних процесів приводить до можливості реалізувати генерацію в ербієвих лазерах, якщо випромінювання накачки виробляє заселення нижнього лазерного рівня N₁. Для цього випадку в системі рівнянь D(t,х) необхідно перенести параметр R₀ з рівняння для х₂ в рівняння для величини х₁, а також змінити енергію фотона кванта накачки. Останні параметри моделі можна залишити без зміни.

На рис. 4.3 наведено характеристики, аналогічні характеристикам рис. (4.2), але для випадку накачування випромінюванням в нижній лазерний рівень. Видно, що динаміка зміни заселеності лазерних рівнів інша. Щільність населеності нижнього лазерного рівня N1 завжди перевищує щільність заселеності рівня N2. Переклад частинок з рівня N1 на верхні рівні в даній моделі здійснюється тільки за рахунок апконверсії. (Це справедливо тільки в рамках наближень, прийнятих для даної моделі. Існує додатковий процес порушення верхніх рівнів іонів ербію з ненульовою ймовірністю, пов'язаний з поглинанням випромінювання накачування безпосередньо з порушеної спочатку рівня N1). Зауважимо, що при рівній повної поглиненої потужності випромінювання накачування, кількість поглинених фотонів для випадку накачування в нижній лазерний рівень буде приблизно в 1,5 рази більше. Щільність потоку випромінювання генерації для даних рис. 4.3 становить S=0/5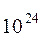1* 1/ 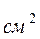с, що май же в 4 рази меньше щільності потоку випромінювання генерації при накачуванні в верхній лазерний рівень.

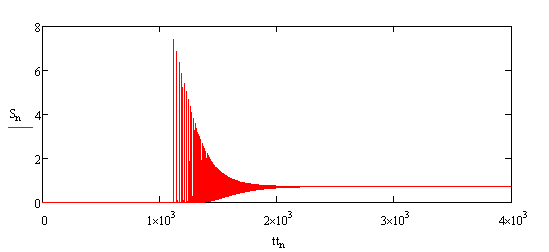
а)

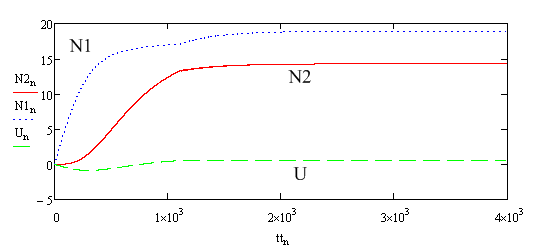
б)

Рис. 4.3 Часові характеристики величин S, N2, N1, U лазера на основі YLF:Er при накачуванні випромінюванням в нижній лазерний рівень N1.

Дата добавления: 2015-07-11