|
Читайте также: |
МОДЕЛЮВАННЯ СТАЦІОНАРНОГО РІВНЯННЯ ШРЕДІНГЕРА
Мета роботи полягає у засвоєні навичок роботи в системі MATLAB та моделювання стаціонарного рівняння Шредінгера.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Розглянемо рішення одновимірного стаціонарного рівняння Шредінгера частинки, яка рухається в одновимірному потенціалі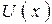 
. При цьому вважатимемо, що його форма має потенціал, представлений на рис. 1: в точках 
, 
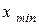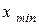потенціал стає нескінченно великим. Це означає, що в точках , розташовані вертикальні стінки, а між ними знаходиться яма кінцевої глибини. Для зручності подальшого рішення запишемо рівняння Шредінгера у вигляді:
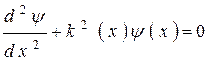, (1.1)
де
. (1.2)
З математичної точки зору завдання полягає у відшуканні власних функцій оператора 
, що відповідають граничним умовам
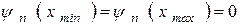, (1.3)
і відповідних власних значень енергії E.
Так як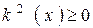 
при 
і 
при 
, 
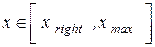, то можна очікувати, що власному рішенню даної задачі відповідає власна функція, що осцилює в класично дозволеної області руху 
(
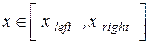) і експоненціально затухаючим в заборонених областях, де 
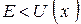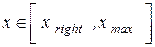(, ), при 
, 
. Оскільки всі стани частки в потенційній ямі опиняються зв'язаними (тобто локалізованими в кінцевої області простору), спектр енергій є дискретним. Частка, що знаходиться в потенційній ямі кінцевих розмірів (
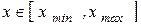при 
, 
при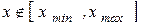 
), має дискретний спектр при 
та безперервний спектр при 
.
Традиційно для рішення задачі про знаходження власних значень рівняння Шредінгера використовується метод пристрілки. Ідея методу пристрілки полягає в наступному. Допустимо, як шукане значення шукається один із зв'язаних станів, тому як пробне початкове значення енергії вибираємо негативне власне значення. Проінтегруємо рівняння Шредінгера яким-небудь відомим чисельним методом на інтервалі 
. В ході інтегрування від 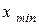в бік більших значень x спочатку обчислюється рішення 
, експоненціально наростаюче в межах класично забороненої області. Після переходу через точку повороту 
, що обмежує зліва область руху дозволену класичною механікою, рішення рівняння стає таким, що осцилює. Якщо продовжити інтеграцію далі за праву точку повороту 
, то рішення стає чисельно нестійким. Це обумовлено тим, що навіть при точному виборі власного значення, для якого виконується умова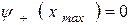 
, рішення в області 
завжди може містити деяку домішку експоненціально зростаючого рішення, що не має фізичного вмісту. Відмічена обставина є загальним правилом: інтеграція по напряму усередину області, забороненою класичною механікою, буде неточним. Отже, для кожного значення енергії розумніше обчислити ще одне рішення 
, інтегруючи рівняння від у бік зменшення x. Критерієм збігу даного значення енергії є збіг значень функцій і у деякій проміжній точці 
. Зазвичай як дану точку вибирають ліву точку повороту . Оскільки функції , є рішеннями однорідного рівняння, їх завжди можна віднормувати так, щоб в точці виконувалась умова 
. Окрім збігу значень функцій в точці для забезпечення гладкості зшивання рішень зажадаємо збігу значень їх похідних 
:
. (1.4)
Використовуючи прості ліву і праву кінечно-різницеві апроксимації похідних функцій , в точці , знаходимо еквівалентну умову гладкості зшивання рішень:
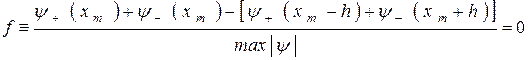, (1.5)
Число 
є масштабуючим множником, який вибирається з умови 
. Якщо точки повороту відсутні, тобто 
, то в якості можна вибрати будь-яку точку відрізку 
. Для потенціалів, що мають більше двох точок повороту і, відповідно, три або однорідних рішень, загальне рішення отримується зшиванням окремих шматків. У описаному нижче документі, для інтеграції диференціального рівняння другого порядку ми використовуємо метод Нумерова. Для здобуття обчислювальної схеми апроксимуємо другу похідну триточковою різницевою формулою:
. (1.6)
З рівняння (16.9) маємо
(1.7)
Підставив (1.6) в (1.7) і перегрупувавши члени, отримуємо
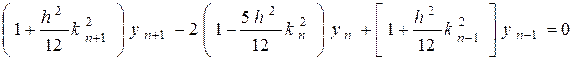. (1.8)
Вирахувавши (1.8) відносно 
або 
, знайдемо рекурентні формули для інтегрування рівняння вперед або назад по x з локальною похибкою 
. Відзначимо, що похибка даного методу виявляється на порядок вище, ніж похибка методу Рунге-Кутта четвертого порядку. Крім того даний алгоритм ефективніший, тому що значення функції 
обчислюються лише у вузлах сітки.
Для знаходження чисельного рішення виявляється зручним провести знерозмірюванне рівняння, використовуючи в якості одиниць виміри відстані а - ширину потенційної ями, в якості одиниц виміру енергії - модуль мінімального значення потенціалу 
. У вибраних одиницях виміру рівняння має вигляд
, (1.9)
де
, 
, 
, 
. (1.10)
Таким чином, обчислювальний алгоритм для знаходження власних функцій і власних значень рівняння Шредінгера реалізується наступною послідовністю дій:
1. Задати вираження, що описує безрозмірний потенціал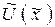 
.
2. Задати значення 
.
3. Задати просторову сітку, на якій проводиться інтегрування рівняння.
4. Задати , .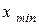
5. Задати початкове значення енергії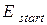 
.
6. Задати кенцеве значення енергії 
.
7. Задати крок зміни енергії 
.
8. Проінтегрувати рівняння для значення енергії 
зліва направо на відрізку 
.
9. Проінтегрувати рівняння для значення енергії зправа наліво на відрізку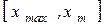 
.
10. Вирахувати значення змінної 
для значения энергии .
11. Збільшити поточне значення енергії на : 
.
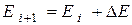12. Проінтегрувати рівняння для значення енергії 
зліва направо на відрізку .
? 13. Проинтегрировать уравнение для значения энергии справа налево на отрезке .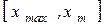
14. Вирахувати значення змінної 
для значения энергии .
15. Порівняти знаки , 
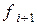
16. Якщо 
і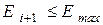 
, збільшити поточне значення енергії на і повторити дії, описані в пп. 8 - 17.
17. Якщо 
, уточнити методом лінійної інтерполяції.
18. Якщо 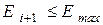, повторити дії, описані в пп. 8 - 18.
19. Якщо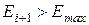 
, закінчити розрахування.
Для реалізації описаного обчислювального алгоритму в пакеті MATLAB необхідно створити три m-файли: 1) файл Num.m, який містить опис функції, що повертає для заданої енергії величину f, обчислювану у відповідності з (5), і значення хвилевої функції у вузлах координатної сітки; 2) файл U.m, який містить опис функції, повертаючий значення потенціалу; 3) файл Elevel.m, який містить опис функції, що повертає власні значення і власні функції рівняння Шредінгера.
% лістинг файла Num.m
function [f,psi]=Num(gamma,E,V,Xmin,Xmax,Ngreed)
% функція, яка повертає для заданої енергії величину f, що обчислюється
% у відповідності з (18), і значення хвильової функції у вузлах
% координатної сітки
% gamma - коефіцієнт, що входить в знерозмірене рівняння
% Шредінгера (1.9)
% E - задане значення енергії
% V - вектор, який містить значення потенціалу в вузлах координатної
% сітки
% Xmin - ліва границя координатної сітки
% Xmax - права границя координатної сітки
% Ngreed - число вузлів координатної сітки
dx=(Xmax-Xmin)/Ngreed;
c=dx.^2*gamma^2/12;
Imatch=1;
psi(1)=0;
psi(2)=9.99999*10^-10;
% інтегрування рівняння Шредінгера зправа наліво
Kim1=c*(E-V(1));
Ki=c*(E-V(2));
for i=2:Ngreed-1
Kip1=c*(E-V(i+1));
if and(Ki*Kip1<=0,Ki>0)
Imatch=i;
i=Ngreed;
End;
if i<=Ngreed-1
psi(i+1)=(psi(i)*(2-10*Ki)-psi(i-1)*(1+Kim1))/(1+Kip1);
if abs(psi(i+1))>=10^10
for k=1:i+1
psi(k)=psi(k)*9.99999*10^-6;
End;
End;
Kim1=Ki;
Ki=Kip1;
End;
End;
if Imatch==1
Imatch=Ngreed-10;
End;
% інтегрування рівняння Шредінгера зліва направо
psi_Left=psi(Imatch);
psi(Ngreed)=0;
psi(Ngreed-1)=9.99999*10^-10;
Kip1=c*(E-V(Ngreed));
Ki=c*(E-V(Ngreed-1));
for i=Ngreed-1:-1:Imatch+1
Kim1=c*(E-V(i-1));
psi(i-1)=(psi(i)*(2-10*Ki)-psi(i+1)*(1+Kip1))/(1+Kim1);
if abs(psi(i))>10^10
for k=Ngreed:-1:i
psi(k)=psi(k)*9.99999*10^-6;
End;
End;
Kip1=Ki;
Ki=Kim1;
End;
if psi_Left<0
for i=Imatch:Ngreed
psi(i)=-psi(i);
End;
End;
psi1=abs(psi);
Psimax=max(psi1);
% обчислення різниці між хвилевими функціями, отриманими
% інтегруванням рівняння Шредінгера зліва направо і справа наліво,
% в вузлі з номером Imatch
f=(psi_Left+psi(Imatch)-(psi(Imatch-1)+psi(Imatch+1)))/Psimax;
% лістинг файла U.m
function z = U(x,Xmin,Xmax)
% функція, що повертає значення потенціалу у вузлах координатної
% сітки
% x - вектор, який містить координати вузлів
% Xmin - ліва границя потенціалу
% Xmax - права границя потенціалу
if and(Xmin<=x,x<=Xmax)
z=-1;
Else
z=10^309;
End;
% лістинг файла Elevel.m
function [EL,Psi]=Elevel(gamma,dE,V,Emax,Xmin,Xmax,Ngreed)
% функція, що повертає власні значення і власні функції
% рівняння Шредінгера
% gamma - коефіцієнт, що входить в знерозмірене рівняння
% Шредінгера
% dE - приріст енергії
% V - вектор, що містить значення потенціалу у вузлах координатної
% сітки
% Emax - максимальне значення енергії
% Xmin - ліва границя координатної сітки
% Xmax - права границя координатної сітки
% Ngreed - число вузлів координатної сітки
Tolf=10^-6;
Emin=-1;
E=Emin+dE;
m=1;
Start=0;
while E<Emax
if Start==0
E1=E;
[f,psi]=Num(gamma,E,V,Xmin,Xmax,Ngreed);
E=E+dE;
F1=f;
Start=1;
End;
E2=E;
[f,psi]=Num(gamma,E,V,Xmin,Xmax,Ngreed);
F2=f;
if F1*F2>0
E1=E;
F1=F2;
E=E+dE;
End;
if F1*F2<0
% уточнення власного значення енергії і обчислення значень
% власної функції у вузлах координатної сітки
a=(E2-E1)/(F2-F1);
E=E1-a*F1;
[f,psi]=Num(gamma,E,V,Xmin,Xmax,Ngreed);
F1=F2;
E1=E2;
EL(m,1)=m;
EL(m,2)=E;
if m==1
Psi0=psi';
Else
Psi0=cat(2,Psi0,psi');
End;
m=m+1;
E=E+dE;
End;
End;
dx=(Xmax-Xmin)/(Ngreed-1);
N1=size(Psi0,2);
% нормування власних хвильових функцій
for i=1:N1
S=Psi0(:,i);
S1=S.^2;
Norm=0;
for j=1:Ngreed-1
Norm=Norm+0.5*(S1(j)+S1(j+1))*dx;
End;
S=S./(Norm^0.5);
if i==1
Psi=S;
Else
Psi=cat(2,Psi,S);
End;
End;
Далі необхідно виконати наступну послідовність команд:
>> Xmin=-0.5; % ліва границя координатної сітки
>> Xmax=0.5; % права границя координатної сітки
>> gamma=20;
>> Ngreed=500; % число вузлів координатної сітки
% обчислення координат вузлів сітки
>> i=1:Ngreed;
>> x(i)=Xmin+(Xmax-Xmin)/(Ngreed-1)*(i-1);
>> dE=10^-3; % приріст енергії
>> Emax=-0; % максимальне значення енергії
>> V(i)=U(x(i),Xmin,Xmax); % обчислення значення потенціалу у вузлах
% координатної сітки
% обчислення власних значень і власних функцій рівняння
% Шредінгера
>> [EL,Psi]=Elevel(gamma,dE,V,Emax,Xmin,Xmax,Ngreed);
>> EL
EL =
1.0000 -0.9751
2.0000 -0.9005
3.0000 -0.7761
4.0000 -0.6020
5.0000 -0.3782
6.0000 -0.1046
% візуалізація власних функцій
>> plot(x(i),Psi(:,1),'k',x(i),Psi(:,2),'--k',x(i),Psi(:,3),'-.k');
>> plot(x(i),Psi(:,4),'k',x(i),Psi(:,5),'--k',x(i),Psi(:,6),'-.k');
Результат виконання описаної послідовності команд представлений
на рис. (1.1), (1.2), (1.3).
Рис. 1.2 Хвильові функції, що відповідають першому, другому і третьому власним значенням енергії
Рис. 1.3 Хвильові функції, відповідні четвертому, п'ятому і шостому власним значенням енергії
Дата добавления: 2015-07-11; просмотров: 50 | Нарушение авторских прав