Лабораторна робота № 2

ОЦІНКА ЕНЕРГІЇ ОСНОВНОГО СТАНУ КВАНТОВОЇ СИСТЕМИ МЕТОДОМ МОНТЕ-КАРЛО

Мета роботи: навчитися оцінювати енергию основного стану квантової системи методом Монте-Карло

ТЕОРЕТИЧНІ ВІДОМОСТІ

В основу методу знаходження енергії і хвильової функції основного стану покладений зв'язок рівняння Шредінгера з процесом дифузії в уявному часі [2—4]. Продемонструємо основні ідеї даного методу на прикладі руху частинки в одновимірному потенціалі, що описується одномірним рівнянням Шредінгера, яке для вільної частинки має вигляд

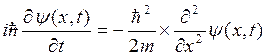(2.1)

Виконавши заміну змінної t→ -i´τћ, отримаємо:

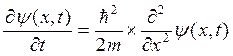(2.2)

Рівняння (2.2) по свій формі збігається з рівнянням дифузії

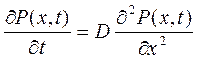(2.3)

де Р(х,t) — щільність вірогідності виявити частинку в момент часу t в точці з координатою х.

Отже, можна інтерпретувати хвильову функцію ψ(х,τ) як щільність вірогідності дифузійного процесу з коефіцієнтом дифузії 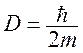. Пригадаємо, що раніше в гл. 12 ми продемонстрували можливість використання методу випадкових блукань для моделювання решень рівняння дифузії. Таким чином, виявлена аналогія між рівняннями, дозволяє замість безпосереднього рішення рівняння Шредінгера шукати рішення задачі про випадкові блукання.

Рівняння Шредінгера відноситься до класу лінійних діфференційних рівнянь в приватних похідних, тому при рішенні задачі можна розглянути рух не одного, а великої кількості пішоходів, що рухаються незалежно один від одного. Для розуміння ролі потенціальної енергії, перепишемо одновимірне рівняння Шредінгера в наступному вигляді:

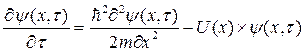(2.4)

За відсутності члена U(x)ψ(x,τ) у правій частині рівняння (2.4), рівняння перетворюється на звичайне рівняння дифузії. З іншого боку, за відсутності в правій частині члена рівняння (2.4) можна трактувати як кінетичне рівняння, що описує процеси, такі як, наприклад, радіоактивний розпад або динаміка чисельності біологічної популяції. Отже, рівняння (2.4) можна трактувати як комбінацію дифузійних процесів, в яких число пішоходів збільшується або зменшується залежно від знаку функції U(х). Відзначимо, що дифузійній інтерпретації потрібно, щоб амплітуда вірогідності була не негативною функцією.

Виконавши заміну змінної t→ -i∙τћ, отримаємо загальне рішення рівняння у вигляді:

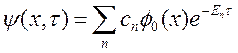(2.5)

З (2.5) видно, що для чималих τ основний вклад в суму дає член, відповідний стану з мінімальною енергією Е₀ (основному стану):

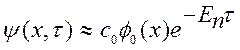(2.6)

а просторова залежність щільності розподілу вірогідності пропорційна власній функції основного стану φо(х).

В той же час рішення у вигляді (2.6) має істотний недолік, що полягає в тому, що

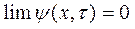(2.7)

для всіх х. Для усунення відміченого недоліку можна відлічувати Е₀ від довільного значення початкової енергії U ref, яка вибирається з умови досягнення стаціонарного розподілу.

Для знаходження формули при оцінці Е₀ перепишемо (2.4) і (2.6) в явному вигляді, ввівши початок відліку енергії в точці U ref:

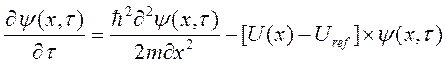(2.8)

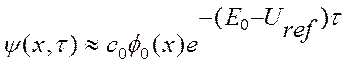(2.9)

Про інтегрувавши по х і врахувавши, що

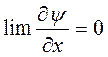
Отримаємо:

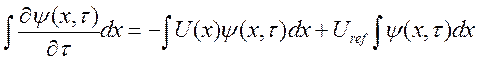(2.10)

Продиференціювавши (1.9) по τ, знайдемо

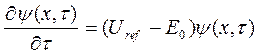(2.11)

Підставивши (2.11) в (2.10), отримуємо:

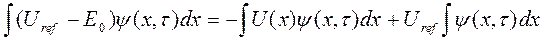(2.12)

Скоротивши в (1.12) члени, пропорційні U ref, отримуємо

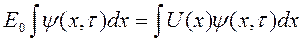(2.13)

звідки

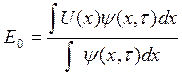(2.14)

Оскільки ψ(x,τ) дорівнює щільності пішоходів n(x,τ) в точці х в момент часу t, для випадку випадкових блукань рівняння (2.14) можна остаточно записати у вигляді

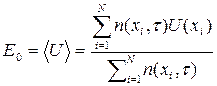(2.15)

де N — кількість пішоходів.

Оцінка Е₀ виходить, як середнє декількох значень τ, що відповідають стаціонарному розподілу.

Хвильова функція основного стану φо(х) є функція розподілу щільності вірогідності пішоходів по вузлах сітки n(xi), обчислювана як середнє декількох значень τ, що відповідають стаціонарному розподілу.

Метод випадкових блукань для знаходження енергії основного стану квантової частинки і відповідної хвильової функції реалізується наступною послідовністю дій.

1. Розміщення N 0 випадковим чином в початковій точці xi.

2. Обчислення опорного потенціалу .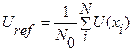

3. Переміщення випадковим чином пішохода вправо або вліво на заданий крок Δs. (Довжина кроку Δs пов'язана з кроком за часом відношенням 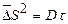, D — коефіцієнт дифузії. У системі одиниць ћ = m = 1, D=0.5)

4. Обчислення 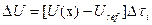і випадкового числа r, рівномірно розподіленого на відрізку [0,1].

5. Якщо ΔU > 0 і r< ΔU, видалити пішохода.

6. Якщо ΔU ≤ 0 і r ≤ -ΔU, добавити пішохода в точку х.

7. Повторити пп. 3-6 для кожного з N 0 пішоходів.

8. Замінити опорний потенціал на

,

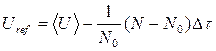де N - нова кількість пішоходів, {U} - середня потенційна енергія N пішоходів, що є оцінкою енергії основного стану.

9. Повторення пп. 3—8 до досягнення енергією стаціонарного значення

10. Повторення пп. 3—9 для здобуття декількох стаціонарних значень енергії.

11. Здобуття усередненого значення енергії по декількох стаціонарних значеннях.

12. Здобуття усередненої функції розподілу щільності вірогідності по декількох стаціонарних значеннях.

Для реалізації описаного алгоритму створимо файл WaIkSh.ni, що містить опис функції, яка повертає середнє значення енергії основного стану і миттєві (на кожному кроці Монте-Карло) значення кількості пішоходів в заданих інтервалах.

% лістинг функції WalkSh.m

function [Em,h]=WalkSh(N,Srange,K,ds,NTrial,Interval)

% функція, яка повертає середнє значення енергії основного

% стану та миттєві (на кожному кроці Монте-Карло) значення

% кількості пішоходів в заданих інтервалах

% N - число пішоходів

% Srange - розмір початкової області розміщення пішоходів

% К - доля невживаних нестаціонарних станів

% ds - розмір кроку пішохода

% NTrial - число випробувань

% Interval - вектор, що містить координати кінців відрізку,

% використовуваних для обчислення щільності розподілу пішоходів

Vref=0;

% ініціалізація початкової конфігурації пішоходів

for i=1:N

Xsite(i)=Srange*(0.5-rand(1));

Vref=Vref+V(Xsite(i));

End;

Vref=Vref/N;

Ninitial=N; % кількість пішоходів на початку випробування

Nwalker=N; % кількість пішоходів в ході випробування

dt=ds.^2; % крок за часом

Nequial=K*NTrial; % номер першого стаціонарного стану

m=1;

for i=1:NTrial

Vsum=0; % повна потенціальна енергія

for j=Ninitial:-1:1

if rand(1)<0.5

Xsite(j)=Xsite(j)+ds;

Else

Xsite(j)=Xsite(j)-ds;

End;

Potential=V(Xsite(j));

dv=Potential-Vref;

if dv<0 % перевірка на додавання пішохода

if rand(1)<-dv*dt

Nwalker=Nwalker+1;

Xsite(Nwalker)=Xsite(j); % новий пішохід

Vsum=Vsum+2*Potential;

Else

Vsum=Vsum+Potential; % додаємо лише енергію старого пішохода

End;

Else

if rand(1)<dv*dt % перевірка на видалення пішохода

Xsite(j)=Xsite(Nwalker);

Nwalker=Nwalker-1;

Else

Vsum=Vsum+Potential;

End;

End;

End;

Vave=Vsum/Nwalker; % середній потенціал

if i>Nequial

E(m)=Vave;

for n=1:Nwalker

X(n)=Xsite(n);

End;

h1=hist(X,Interval);

if m==1

h=h1';

Else

h=cat(2,h,h1');

End;

m=m+1;

End;

Vref=Vave-(Nwalker-N)/(N*dt); % новий опорний потенціал

End;

Em=mean(E);

function z=V(x);

% функція, що описує потенціал

z=0.5*x.^{^}2;

>> N=1000; % початкова кількість пішоходів

>> ds=0.1; % довжина кроку пішохода

>> NTrial=1000; % число випробувань

>> Srange=2; % розмір початкової області розміщення пішоходів

>> K=0.2; % доля невживаних нестаціонарних станів

>> Ni=40; % кількість інтервалів, використовуваних для обчислення

% щільності розподілу пішоходів

% обчислення границь інтервалів

>> i=1:Ni+1;

>> Interval(i)=-2*Srange+(4*Srange/Ni*(i-1));

% обчислення усередненої енергії основного стану

% і обчислення миттєвих (на кожному кроці Монте-Карло)

% хвильових функцій

>> [A h]=WalkSh(N,Srange,K,ds,NTrial,Interval);

>> A % енергія основного стану

ans =

0.4978

% обчислення значень усередненої хвильової функції

>> Nx=size(h,1)

>> Ny=size(h,2)

>> for i=1:Nx

for j=1:Ny

A(j)=h(i,j);

End;

A1(i)=sum(A);

End;

% візуалізація потенціалу і усередненої хвильової функції

>> Ni=500;

>> dx=(max(Interval)-min(Interval))/(Ni-1);

>> i=1:Ni;

>> x(i)=min(Interval)+dx*(i-1);

>> plot(x,0.5*x.^{^}2,'k',Interval,A1/max(A1),'k')

Результати виконання описаної послідовності команд передcтавлені на рис. (2.1), (2.2).

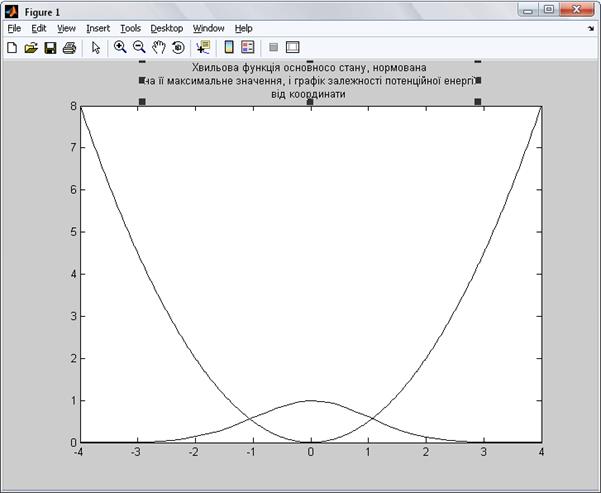
Рис. 2.2 Хвильова функція основного стану, нормована на її максимальнезначення, і графік залежності потенційної енергії від координати

Дата добавления: 2015-07-11