Лабораторна робота № 3

ОЦІНКА ЕНЕРГІЇ ОСНОВНОГО СТАНУ КВАНТОВОЇ СИСТЕМИ ВАРІАЦІЙНИМИ МЕТОДАМИ МОНТЕ-КАРЛО

Мета роботи: навчитися оцінювати енергию основного стану квантової системи варіаційними методами Монте-Карло.

ТЕОРЕТИЧНІ ВІДОМОСТІ

Альтернативний підхід до оцінки енергії основного стану квантових систем полягає у використанні варіаційного методу, що дозволяє отримати оцінки верхніх границь значень енергії основного стану. Даний варіаційний метод знаходить багаточисельні застосування в атомній фізиці, молекулярній фізиці, ядерній фізиці і фізиці середовищ, що конденсують. Детальний розгляд багаточисельних прикладів, що відносяться до перерахованих вище розділів фізики, виходить за рамки нашої книги, тому далі ми обмежуємося обговоренням основних ідей варіаційного методу Монте-Карло.

Розглянемо квантову систему, що описується оператором Гамільтона Ĥ. Варіаційний принцип стверджує, що для довільної функції φ(х) виконується нерівність

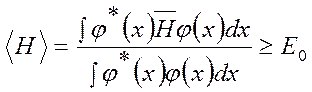(3.1)

де Е₀ – енергія основного стану системи.

Нерівність (3.1) перетворюється на точну рівність лише у тому випадку, коли функція φ(х) буде власною функцією оператора Ĥ, яка відповідає власному значенню Е_0. Величину {Н} можна трактувати як математичне сподівання повної енергії для наближеної хвильової функції φ(х).

Нерівність (3.1) є основою варіаційного методу. Механізм реалізації даного методу полягає у фізично обгрунтованому виборі пробної функції, залежної від декількох параметрів: обчисленні {Н} відповідно до (3.1), варіюванні одного або більш параметрів до тих пір доки не буде досягнуте мінімальне значення {Н}. Дане значення є верхньою границею дійсного значення енергії основного стану.

Розглянемо реалізацію варіаційного методу Монте-Карло на прикладі одновимірної системи. Введемо просторову тимчасову сітку хі = = іΔх, де Δх - крок сітки, у вузлах якої обчислюватимемо значення функції.

Алгоритм варіаційного методу Мотне-Карло реалізується наступною послідовністю дій:

1. Вибрати фізично обгрунтовані значення пробної функції φ(х) в точках хі.

2. Вибрати випадкову точку хі, і змінити значення φі= φ(хі) на випадкову величину Δφ Є [-δ; δ].

3. Обчислити зміну енергії ΔЕ для {Н}.

4. ЯкщоΔ Е ≤ 0, прийняти виконану зміну φі.

5. Якщо Δ Е > 0, відхилити виконану зміну φі.

6. Повторювати пп. 2-5 до досягнення постійного (із заданою точністю) значення {Н}.

Розглянемо реалізацію описаного алгоритму в пакеті MATLAB для випадку, коли хвильова функція є симетричною. Далі приводиться лістинг m-файлу Variation.m, що містить опис функції, яка повертає верхнію границю значення енергії основного стану, відповідну хвильову функцію, і миттєві (на кожному кроці ітераційного процесу) значення енергії.

% листинг файла Variation.m

function [Em,psi,W] = Variation(Xmax,delta,N)

% функція, що повертає верхню границю значення енергії основного

% стану, відповідну хвильову функцію, і миттєві

% (на кожному кроці ітераційного процесу значення енергії)

% Хmax – максимальне значення координати

% delta - максимальна зміна хвильової функції

% N - число вузлів координатної сітки в кожному напрямі

dx=Xmax/N; % число вузлів координатної сітки в кожному напрямі delta=2*delta;

Nmove=1000*N; % число кроків ітераційного процесу

Norm=0;

k=1;

% обчислення значень початкового наближення

for i=1:2*N+1

psi(i)=f(-Xmax+dx*(i-1));

End;

Norm=sum(psi.^{^}2); % нормований множник

% обчислення початкової енергії

E=0;

for i=N+2:2*N

x=-Xmax+(i-1)*dx;

pe=psi(i)*psi(i)*V(x); % потенціальна енергія

ke=0.5*psi(i)*(2*psi(i)-psi(i+1)-psi(i-1))/dx^{^}2; % кінетична енергія E=E+2*(pe+ke);

End;

E=E+E*V(0)*psi(N+1)^{^}2;

E=E+0.5*psi(N+1)*(2*psi(N+1)-psi(N+2)-psi(N))/dx^{^}2;

% варіювання хвильової функції

Ecum=0;

for Imove=1:Nmove

i=floor((N-1)*rand(1))+N+2; % координата точки

dpsi=delta*(rand(1)-0.5); % зміна хвильової функції

Psi_Trial=psi(i)+dpsi; % пробне значення хвильової функції

% у і-м вузлі обчислення зміни енергії, обумовлене

% зміною хвильової функції в і-ом вузлі

dpsi2=Psi_Trial*Psi_Trial-psi(i)*psi(i);

dV=dpsi2*V(-Xmax+(i-1)*dx); % зміна потенціальної енергії dK=(dpsi2-dpsi*(psi(i+1)+psi(i-1)))/dx^{^}2; % зміна

% кінетичної енергії

if i==N+1

Etrial=E+dK+dV;

Norm_Trial=Norm+dpsi2;

Else

Etrial=E+2*(dV+dK);

Norm_Trial=Norm+2*dpsi2;

End;

dE=Etrial/Norm_Trial-E/Norm;

if dE<0 % прийняття зміни хвильової функції

psi(i)=Psi_Trial;

psi(2*N+2-i)=Psi_Trial;

Norm=Norm_Trial;

E=Etrial;

End;

Ecum=Ecum+E/Norm;

W(Imove)=E/Norm;

End;

Em=Ecum/Nmove;

functionz = f(x)

% функція, що описує початкове наближення

z=exp(-x.^{^}2);

function z = V(x)

% функція, що описує потенціал

z=0.5*x.^{^}2;

Далі необхідно виконати наступну послідовність команд:

>> Xmax=4; % максимальне значення координати

>> N=40; % число вузлів в кожному напрямі осі оХ

>> delta=0.1; % максимальна зміна хвильової функції

>> [Em psi W] = Variation(Xmax,delta,N);

% візуалізація хвильових функцій і залежності миттєвого

% значення енергії від номера кроку ітерації рис. (3.1)

>> Ni=1000;

>> i=1:Ni;

>> dx=Xmax/Ni;

>> x(i)=-Xmax+2*dx*i;

>> j=1:length(psi);

>> X(j)=-Xmax+2*Xmax/length(psi)*(j-1);

>> plot(X(j),psi(j),'k',x,exp((-x.^{^}2)/2),'-.k',x,exp(-x.^{^}2),'--k');

>> plot(W,'k'); plot(W,'k');axis([0 length(W) 0.5 0.65])

Результати виконання описаної послідовності команд передcтавлені на рис. (3.1), (3.2), (3.3).

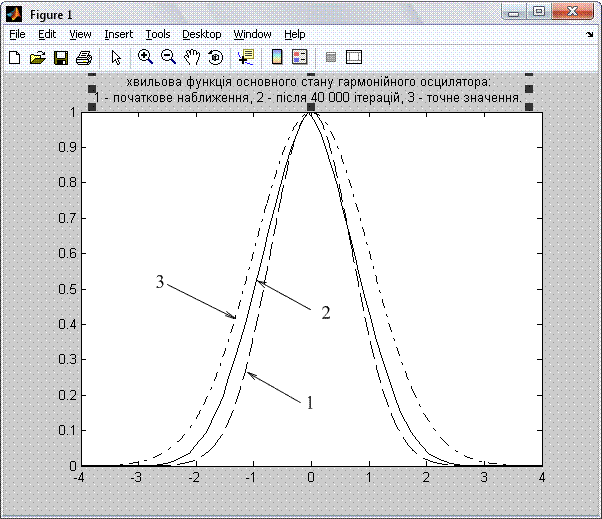
Рис. 3.2 Хвильова функція основного стану гармонійного осцилятора: 1 - початкове наближення, 2 - після 40 000 ітерацій, 3 - точне значення.

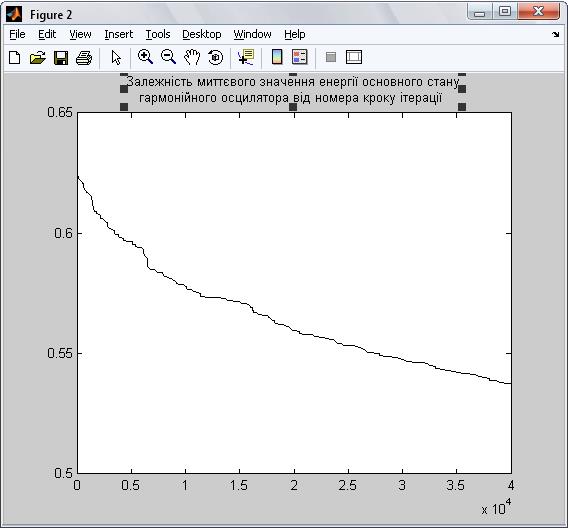
Рис. 3.3 Залежність миттєвого значення енергії основного стану

гармонійного осцилятора від номера кроку ітерації

Дата добавления: 2015-07-11