Квадратичная форма и ее приведение к каноническому виду.

Пусть 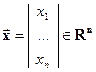, -вещественная симметричная матрица,

В общем случае, скалярное произведение векторов каждому вектору ставит в соответствие вещественное число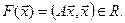

Определение. Пусть A_n – вещественная симметричная матрица и x=[ x₁,…,x_n ]^T∊Rⁿ.
Функция (отображение, однозначное соответствие) F

(1)

которая каждому вектору ∊Rⁿ (точке M()) ставит в соответствие вещественное число , называется квадратичной формой (КФ), матрица А_n – матрицей квадратичной формы, значением функции КФ в точке .

Так как матрица А_n симметричная (a_ik=a_ki), КФ можно записать в виде суммы

,

в каждом слагаемом которой сумма степеней координат вектора равна 2.

ЭКЗ: Записать в общем виде КФ и её матрицу для n=3.

Теорема. Пусть:

(1) ; (2) - её собственные значения и B_ОНБ=[ - ортонормированный базис, в котором вектор имеет координаты Тогда

«В системе координат, определяемой ортонормированным базисом из собственных векторов матрицы A_n, квадратичная форма имеет канонический вид:

(2)

Дата добавления: 2015-07-11