Собственные значения матрицы A.

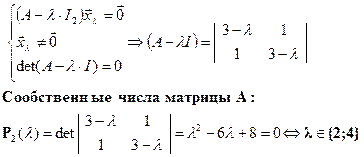
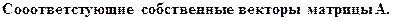
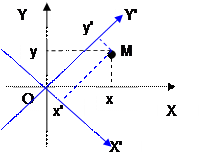
Определим на плоскости (новую) прямоугольную систему координат, например, так:
X’OY’(e₁,e₂): OX’(e₁)∧ OY’(e₂)

2.2 Найдем уравнения, связывающие координаты точки М плоскости в двух координатных системах XOY(i,j), X’OY’(e₁,e₂), записав радиус-вектор точки в этих системах: 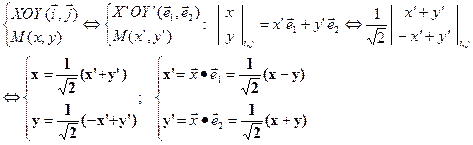(2)

Запишемквадратичную форму и уравнение кривой второго порядка в новой системе координат X’OY’(e₁,e₂).

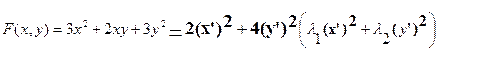
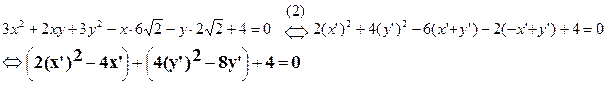
2.3 Выделим в полученном уравнении «полные квадраты» по x’ и y’

,

и получим уравнение кривой в системе X’OY’:

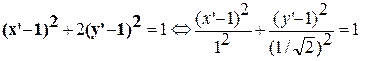(3)

Выполним «преобразование параллельного переноса» системы X’OY’ в точку С(1,1): X’OY’→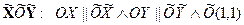

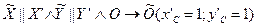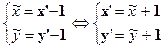ó (4)

В системе координат 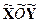(e₁,e₂) получим каноническое уравнение заданной кривой второго порядка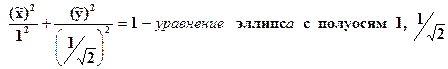

Изобразим схематически график этой кривой на координатной плоскости.

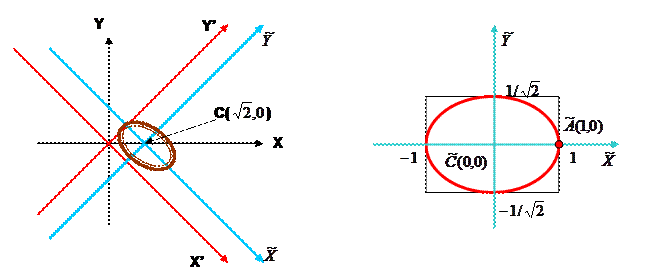
2.4 Очевидно, что точка лежит на эллипсе. Используя соотношения (4) и (2), найдем ее координаты в двух других системах координат:

A(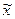 =1; ) ↔ A(x’=2; y’=1) ↔ A()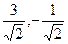

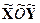X’OY’ XOY

и убедимся в том, что координаты 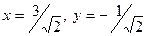удовлетворяют Уравнению (1): [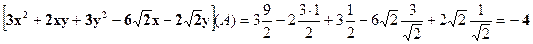

РЕЗУЛЬТАТЫ:

1) XOY: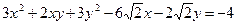

2) X’OY’ (e₁,e₂):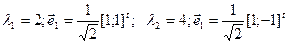

3)

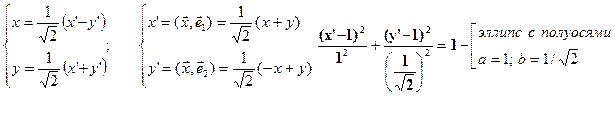
4)

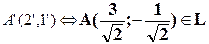
Замечание. Уравнение ax² + bxy + cy² + dx + ey + f=0 определяет на плоскости:

· параболу, если одно из собственных чисел матрицы К₂ равно нулю (l₁=0;l₂¹0).

· Эллипс, если собственные числа матрицы к.ф. одного знака (l₁ ∙l₂>0).

· Гиперболу, если собственные числа матрица к.ф. разного знака (l₁ ∙l₂>0).

Дата добавления: 2015-07-11