Корреляционно-регрессивный анализ (КРА).

Одной из задач статистики является изучение существующих взаимосвязей между различными социально-экономическими явлениями и процессами.

При изучении этих взаимосвязей выявляются причинно-следственные отношения между явлениями или их признаками, при которых изменение причины приводит к изменению следствия. Поскольку на одно и то же социально-экономическое явление могут оказывать влияние различные факторы, то необходимо определить воздействие главных факторов, абстрагируясь от второстепенных. Признаки по их влиянию для изучения взаимосвязей подразделяются на факторные и результативные. Признаки, которые оказывают влияние на другие, связанные с ними признаки, называются факторными [х]. Признаки, которые изменяются под воздействием факторных, называются результативные [y_x].

Регрессионный анализ заключается в определении аналитического выражения связи между изучаемыми признаками, а корреляционный анализ состоит в определении тесноты связи между этими признаками. Различают виды зависимости между признаками: функциональную и стохастическую. При функциональной зависимости каждому значению факторного признака соответствует только одно значение результативного признака. При стохастической зависимости каждому значению факторного признака могут соответствовать 2 и более значений результативного признака. Частным случаем стохастической зависимости является корреляционная связь.

Различают виды корреляционной зависимости между признаками:

· парная корреляция, при которой изучается зависимость одного результативного признака от одного факторного признака или связь между двумя факторными признаками

· частная корреляция, при которой изучается зависимость одного результативного признака от одного факторного признака, при фиксированном значении других факторных признаков

· множественная корреляция, при которой изучается зависимость одного результативного признака от двух и более факторных признаков

Связи между признаками классифицируются по аналитическому выражению, направлению и степени тесноты. По аналитическому выражению различают линейную и нелинейную связь. Связь линейная. Если он может быть выражена с помощью линейной функции 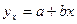, в противном случае связь считается нелинейной. По направлению связи различают прямую и обратную связь. Прямая связь, при которой с увеличением (уменьшением) значений факторного признака, значения результативного признака увеличиваются (уменьшаются). В случае обратной связи между признаками, значение результативного признака изменяется под воздействием факторного в противоположном направлении. Степень тесноты связи между признаками изучается с помощью величины корреляционного отношения – [ 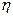]. 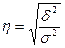, где 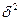- межгрупповая дисперсия, 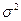- общая дисперсия; 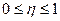; 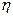=1 – сильная связь между признаками; 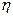=0 – отсутствие связи.

В случае линейной зависимости между двумя признаками вместо корреляционного отношения вычисляют линейный коэффициент корреляции [r].

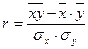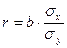; ; где 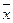- средняя величина факторного признака; 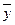- средняя величина результативного признака; 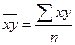(n – число пар значени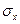й); и 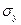- среднее квадратическое отклонение в ряду факторного и результативного признаков; b – параметр линейной функции, выражающий зависимость результативного признака от факторного.

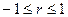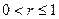: - прямая связь между признаками; 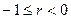- обратная связь. В зависимости от величины линейного коэффициента корреляции различают следующие виды связи между признаками:

значение	комментарий
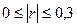
	связь отсутствует
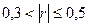
	связь слабая
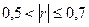
	связь умеренная
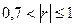
	связь сильная

Параметр “ b ” – показывает на сколько, в среднем, изменяется значение результативного признака при изменении факторного признака на 1 единицу.

Пример: По имеющимся данным составим уравнение линейной функции, выражающее зависимость среднемесячной заработной платы от уровня производительности труда в 5 отраслях промышленности в РФ за 2002 год:

Отрасль промышленности	Уровень производительности труда (млн. руб. на 1 работника), Х	Размер среднемесячной зарплаты (тыс. руб.), Y	Х^2	ХY	Y^2
Электроэнергетика	0.916	7,49	0,839	6,86	56,1001
Топливная	1,450	12,70	2,1025	18,415	161,29
Черная металлургия	0,684	5,92	0,468	4,049	35,0464
Цветная металлургия	0,780	9,48	0,6084	7,3944	89,8704
Машиностроение	0,322	4,18	0,104	1,346	17,4724
Итого:	4,152	39,77	4,1219	38,0644	359,7793

Для определения параметров a и b линейной функции, составляют систему уравнений:

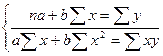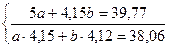; ; a=1,74; b=7,48; 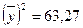; y=1,74+7,48х; 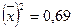; ; 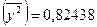; 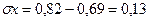r=0,93 – связь очень сильная и прямая.

В некоторых случаях для определения степени тесноты связи между двумя признаками вычисляют ранговые коэффициенты связи Спирмена и Кендалла. Ранжирование – процедура упорядочения объектов изучения в порядке возрастания или убывания количественных значений. Коэффициент корреляции рангов (коэффициент Спирмена):

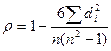, где 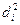- квадрат разности рангов; n – число наблюдений (число пар рангов).

Пример:

Отрасли промышленности	X	Y	Rx	Px	di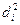
Электроэнергетика	0,916	7,49
Топливная	1,450	12,70
Черная М.	0,684	5,92
Цветная М.	0,780	9,48			-1
Машиностроение	0,322	4,18
Итого:

1) Значения факторного признака ранжируют и ранги по Х записывают строго в порядке возрастания количественных значений.

2) Значения результативного признака записывают строго в порядке возрастания.

3) Находят разность рангов: .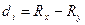

4) Полученные разности возводят в квадрат и рассчитывают их сумму.

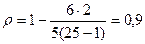
Дата добавления: 2015-07-11