
|
Читайте также: |
При нарушениях равновесия в средах возникают потоки тепла, либо массы, либо импульса и т.п. В связи с этим, соответствующие процессы носят название явлений переноса. Явления переноса представляют собой необратимые процессы.
Введем некоторую скалярную величину  , которая характеризует некоторое молекулярное свойство, отнесенное к одной молекуле. Этим свойством может быть энергия, импульс, концентрация, электрический заряд и т.д.
, которая характеризует некоторое молекулярное свойство, отнесенное к одной молекуле. Этим свойством может быть энергия, импульс, концентрация, электрический заряд и т.д.
Известно, что градиентом какой-либо величины (скалярной)  , зависящей от координат, называется вектор, характеризующий быстроту изменения этой величины в пространстве. Этот вектор направлен в сторону наиболее быстрого возрастания
, зависящей от координат, называется вектор, характеризующий быстроту изменения этой величины в пространстве. Этот вектор направлен в сторону наиболее быстрого возрастания  и численно равен быстроте этого возрастания.
и численно равен быстроте этого возрастания.
Если в равновесном состоянии величина  постоянна по объему, то при наличии градиента
постоянна по объему, то при наличии градиента  , имеет место движение этой величины в направлении его уменьшения.
, имеет место движение этой величины в направлении его уменьшения.
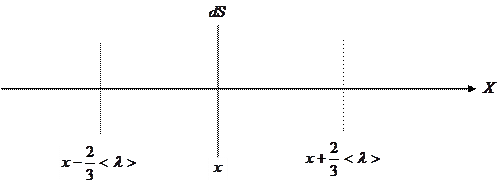 |
 происходит в одном направлении, вдоль которого направим ось
происходит в одном направлении, вдоль которого направим ось 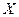 . То есть, пусть ось
. То есть, пусть ось 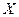 направлена вдоль градиента
направлена вдоль градиента  . Выделим в среде площадку
. Выделим в среде площадку 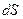 , перпендикулярную к оси
, перпендикулярную к оси 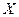 (рис.1).
(рис.1).
Рис.3. К выводу общего уравнения переноса
Площадку 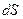 пересекают молекулы, пришедшие со всевозможных направлений и пересекающие ее в направлении отрицательных значений оси
пересекают молекулы, пришедшие со всевозможных направлений и пересекающие ее в направлении отрицательных значений оси 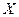 . Число молекул в объеме
. Число молекул в объеме 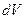 равно
равно 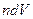 , где
, где  – концентрация молекул вещества. Частица движется со средней скоростью
– концентрация молекул вещества. Частица движется со средней скоростью 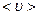 и, следовательно, проходит среднюю длину свободного пробега
и, следовательно, проходит среднюю длину свободного пробега  за время
за время 
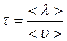 . Поэтому средняя частота столкновений (среднее число столкновений за одну секунду) равна
. Поэтому средняя частота столкновений (среднее число столкновений за одну секунду) равна 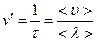 . В течение времени
. В течение времени 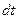 число молекул
число молекул 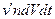 из данного объема в результате столкновений летят изотропно по всевозможным направлениям, в том числе и в направлении площадки
из данного объема в результате столкновений летят изотропно по всевозможным направлениям, в том числе и в направлении площадки 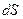 , которая видна из элемента объема
, которая видна из элемента объема 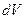 под углом
под углом 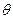 . Число молекул, пересекших площадку
. Число молекул, пересекших площадку 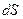 и на пути от элемента объема
и на пути от элемента объема 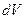 не испытавших ни одного последующего столкновения, равно:
не испытавших ни одного последующего столкновения, равно:
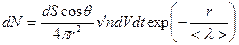 , (1)
, (1)
где 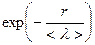 – множитель, который учитывает выбывание молекул из пучка из-за столкновений с другими молекулами;
– множитель, который учитывает выбывание молекул из пучка из-за столкновений с другими молекулами;
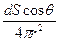 – множитель, который определяет число молекул, приходящихся на данный телесный угол;
– множитель, который определяет число молекул, приходящихся на данный телесный угол;
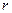 – расстояние от объема
– расстояние от объема 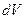 до центра площадки
до центра площадки 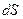 .
.
Поток числа молекул, пересекающих поверхность в единицу времени, равен:
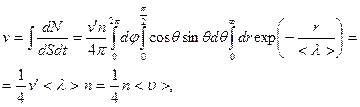 (2)
(2)
где  – концентрация молекул вещества,
– концентрация молекул вещества,
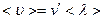 – средняя скорость молекул вещества,
– средняя скорость молекул вещества,
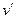 – среднее число столкновений в секунду,
– среднее число столкновений в секунду,
 – средняя длина свободного пробега.
– средняя длина свободного пробега.
Теперь вычислим среднее расстояние вдоль оси 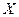 , которое проходят молекулы, пересекающие площадку
, которое проходят молекулы, пересекающие площадку 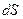 после последнего столкновения. Из теории вероятности известно, что среднее значение непрерывно изменяющейся величины равно
после последнего столкновения. Из теории вероятности известно, что среднее значение непрерывно изменяющейся величины равно
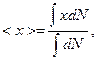 (3)
(3)
где  дается формулой (1). В результате интегрирования (3) выражение для среднего расстояния, пробегаемого молекулами, пересекающими площадку
дается формулой (1). В результате интегрирования (3) выражение для среднего расстояния, пробегаемого молекулами, пересекающими площадку 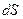 (рис.1) после последнего столкновения примет вид:
(рис.1) после последнего столкновения примет вид:
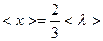 , (4)
, (4)
где  – средняя длина свободного пробега молекулы.
– средняя длина свободного пробега молекулы.
Запишем  на расстоянии
на расстоянии 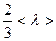 от площадки
от площадки 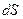 с учетом того, что эта величина
с учетом того, что эта величина 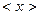 в большинстве случаев достаточно мала и ограничившись первым членом разложения в ряд Тейлора в точке
в большинстве случаев достаточно мала и ограничившись первым членом разложения в ряд Тейлора в точке  :
:
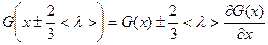 . (5)
. (5)
Поток числа молекул в направлении оси 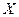 , согласно формуле (2) равен
, согласно формуле (2) равен 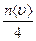 . Следовательно, поток
. Следовательно, поток  сквозь площадку
сквозь площадку 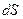 в направлении отрицательных значений оси
в направлении отрицательных значений оси 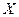 равен
равен

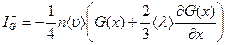 , (6)
, (6)
а в направлении положительных значений оси 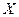 дается выражением
дается выражением
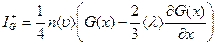 , (7)
, (7)
Следовательно, суммарный поток в положительном направлении оси 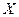 в точке
в точке  имеет вид
имеет вид
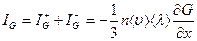 , (8)
, (8)
где  – концентрация молекул вещества,
– концентрация молекул вещества,
 – средняя скорость молекул вещества,
– средняя скорость молекул вещества,
 – средняя длина свободного пробега молекулы,
– средняя длина свободного пробега молекулы,
 – частная производная величины
– частная производная величины  по
по  .
.
Уравнение (8) является основным уравнением процессов переноса количества  .
.
Здесь использован символ частной производной, поскольку величина  зависит и от времени
зависит и от времени 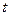 и от координаты
и от координаты  .
.
Выражение (8) можно легко обобщить на случай трехмерного пространства:
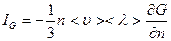 , (9)
, (9)
где 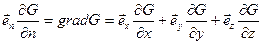 , (10)
, (10)
где 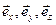 – единичные векторы, направленные по осям прямоугольной системы координат;
– единичные векторы, направленные по осям прямоугольной системы координат;
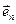 – единичный вектор, направленный по нормали в сторону возрастания
– единичный вектор, направленный по нормали в сторону возрастания  .
.
Дата добавления: 2015-07-11; просмотров: 219 | Нарушение авторских прав