Теория метода

Найдем распределение температур в веществе, находящемся между двумя большими плоскими параллельными пластинами, если последние поддерживают при температурах и , расстояние между ними равно и теплопроводность вещества . То есть, найдем зависимость температуры вещества (газа) между пластинами от расстояния от пластины с меньшей температурой.

Пусть – температура верхней пластины, – температура нижней пластины, - расстояние между ними (рис.4). Причем .

Рассмотрим в веществе, находящемся между пластинами, элементарный слой с некоторой температурой на расстоянии от пластины с температурой . Следовательно, расстояние от слоя до пластины с температурой будет равно .

Рис.4. К нахождению распределения температур в веществе, находящемся между двумя параллельными пластинами.

Считая, что температура зависит только от одной координаты из уравнения (13) получаем, что плотность теплового потока равна

. (23)

Как было показано ранее (формулы (16),(17)) или , где . Тогда в соответствии с формулой (23) можно записать:

. (24)

Проинтегрировав (24) по температуре от до и по от до , находим зависимость температуры от расстояния :

,

,

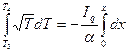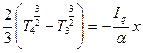. (25)

Проинтегрировав (24) по температуре от до и по от до , выразим отношение :

,

. (26)

Подставляя выражение (26) в формулу (25), получим:

, (27)

где – температура верхней пластины,

– температура вещества между пластинами,

– температура нижней пластины,

– расстояние между пластинами,

– расстояние от пластины с температурой .

Теперь найдем коэффициент теплопроводности вещества, находящегося между двумя плоскими параллельными пластинами.

Плотность теплового потока от пластины с большей температурой к пластине с меньшей температурой выражается формулой (23). По определению, плотность теплового потока – это количество теплоты, проходящее в единицу времени через единицу площади поверхности:

, (28)

где 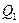– количество тепла, испускаемое нагретой пластиной в направлении холодной;

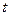– время прохождения тепла через вещество;

– площадь поверхности, через которую проходит теплота.

Поскольку расстояние между пластинами много меньше их линейных размеров, изменение температуры на единицу длины (в среде) в формуле (23) можно представить, как

, (29)

где – разность температур между пластинами,

– температура верхней пластины (нагретой),

– температура нижней пластины (холодной),

– расстояние между пластинами.

Тогда, подставляя (28) и (29) в (23), и, учитывая, что знак “–“ выражает направление переноса тепла от области с большей температурой к области с меньшей температурой, тогда как градиент направлен в сторону возрастания этой величины, получим, что коэффициент теплопроводности вещества равен:

. (30)

Общее количество тепла, испускаемое нагретой пластиной равно

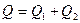, (31)

где 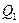– количество тепла, испускаемое нагретой пластиной в направлении холодной;

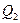– количество тепла, теряемое нагретой пластиной за счет теплообмена с окружающей средой.

Из (31) следует что

, (32)

где – коэффициент, равный отношению количества тепла, испускаемого нагретой пластиной в направлении холодной, к общему количеству тепла, испускаемого нагретой пластиной.

По закону Джоуля – Ленца:

, (33)

где – сопротивление нагретой пластины;

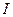– сила тока в цепи;

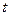– время протекания тока через нагретую пластину.

Таким образом, из формул (33), (32) и (30), учитывая, что время прохождения тепла через вещество равно времени протекания тока через нагретую пластину, получаем, что коэффициент теплопроводности вещества, находящегося между двумя параллельными пластинами равен

, (34)

где – сопротивление нагретой пластины;

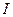– сила тока в цепи;

– площадь поперечного сечения поверхности;

– коэффициент, равный отношению количества тепла, испускаемого нагретой пластиной в направлении холодной, к общему количеству тепла, испускаемого нагретой пластиной;

– расстояние между пластинами;

– температура верхней пластины (нагретой);

– температура нижней пластины (холодной).

Для установки, используемой в работе:

; ; ; .

Порядок выполнения задания

1. Переместить среднюю термопару в нижнее положение (при этом она касается нижней холодной пластины), поворачивая регулятор “ высота “ против часовой стрелки до упора. Убедиться, что тумблер “ нагрев “ переключен в нижнее положение (нагрев отсутствует). Перевести установку на ручной режим работы нагревателя тумблером “ АВТ “-“ РУЧН “. Установить силу тока, протекающего через нагреватель, равную 0,9А регулятором “ ток нагрева “. Как только температура нагревателя (T₅) возрастет до 80˚С, сразу уменьшить ток до 0,6А и выждать пока установится температура нагревателя (около 10 мин).

Соответствие каналов прибора: Т₅ – температура нагревателя, Т₄ – подвижная термопара, Т₃ – холодная пластина.

2. Измерить температуру воздуха между пластинами в 10 различных точках, каждый раз поднимая среднюю термопару на 2 мм вверх. При этом каждый раз проводить измерения температуры холодной пластины . После каждого перемещения термопары необходимо выждать 2мин для установления теплового равновесия и только после этого снимать показания с приборов. Результаты измерений занести в таблицу:

№	, мм	Т5, ˚С	Т4, ˚С	, ˚С	, ˚С

3. На основе проведенных измерений найти распределение температур в воздухе, находящемся между двумя пластинами, поддерживаемыми при постоянных температурах, т.е. проверить зависимость температуры воздуха между пластинами от расстояния от холодной пластины. Построить график .

4. Построить график , используя формулу (27). Для этого предварительно рассчитать и занести в таблицу.

5. Сравнить экспериментальную и теоретическую зависимости .

6. Рассчитать коэффициент теплопроводности воздуха находящегося между пластинами по формуле (34), для чего использовать данные измерений температуры нижней пластины, температуры верхней пластины и силы тока, протекающего через нагреватель.

7. Сравнить полученное значение æ для воздуха с табличным.

8. Сделать вывод о проведенной работе.

Контрольные вопросы

1. Как получить основное уравнение процессов переноса?

2. Что понимают под явлением теплопроводности?

3. Сформулируйте закон Фурье для теплопроводности газов.

4. Что выражает знак “–“ в уравнении Фурье для теплопроводности газов?

5. Каков физический смысл коэффициента теплопроводности, что он характеризует?

6. От каких факторов зависит и от каких не зависит коэффициент теплопроводности газов? Какова его связь с другими коэффициентами, характеризующими процессы переноса?

7. Каково распределение температур в газе, находящемся между двумя пластинами, поддерживаемыми при различных температурах?

8. Выведите формулу для расчета коэффициента теплопроводности вещества, находящегося между двумя параллельными пластинами.

ЛИТЕРАТУРА:

1. Астахов А.В. Курс физики, том 1: Механика // Кинетическая теория материи. – М.: Наука, 1977г. – 384с.

2. Кикоин А.К., Кикоин И.К. Молекулярная физика. – М.: Наука, 1976г. – 480с.

3. Матвеев А.Н. Молекулярная физика. – М.: Высшая школа, 1987г. – 360с.

4. Сивухин Д.В. Общий курс физики, том 2: Термодинамика и молекулярная физика. – М.: Наука, 1990г. – 592с.

5. Савельев И.В. Курс общей физики, кн.3: Молекулярная физика и термодинамика. – М.: Наука: Физматлит, 1998г. – 208с.

6. Телегин А.С., Швыдкий В.С., Ярошенко Ю.Г. Тепло-массоперенос: Учебник для вузов. – М.: Металлургия, 1995 г. – 400 с.

7. Луканин В.Н. Теплотехника: Учебник для вузов. – М.: Высшая школа, 1999г. – 671с.

8. Беляев Н.М., Рядно А.А. Методы теории теплопроводности. – М.: Высшая школа, 1982г. – 328с.

9. Сорокин С.И. Теория теплопроводности. – Саратов: Университетское, 1984г. – 164 с.

Дата добавления: 2015-07-11