Коэффициент теплопроводности газов

Коэффициент пропорциональности в уравнении Фурье для теплопроводности (15) – это и есть коэффициент теплопроводности. Он является физическим параметром, характеризующим интенсивность процесса теплопроводности в веществе, т.е. скорость переноса тепла.

Физический смысл коэффициента теплопроводности вытекает непосредственно из закона Фурье (15): коэффициент теплопроводности численно равен плотности теплового потока при градиенте температуры, равном единице. Это означает, что в случае однородного изотропного тела коэффициент теплопроводности численно равен количеству теплоты, проходящему через единицу поверхности в единицу времени вследствие теплопроводности при перепаде температуры на единицу длины нормали, равном одному градусу. В случае изотропной среды, когда величина коэффициента не зависит от направления, векторы и 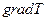лежат на одной прямой, но направлены в противоположные стороны.

Размерность коэффициента теплопроводности в системе СИ – ватт на метр-кельвин: .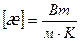

Теплопроводность зависит от агрегатного состояния вещества, его состава, чистоты, температуры, давления и других факторов.

Что касается зависимости от агрегатного состояния, то теплопроводность газов при нормальных условиях обычно в несколько десятков и сотен раз меньше теплопроводности жидкостей, и в сотни тысяч и миллионы раз меньше, чем теплопроводность твердых тел. Численное значение для воздуха при нормальных условиях составляет .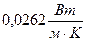

Из уравнения (12) видно, что коэффициент теплопроводности газов

, (16)

где – концентрация молекул вещества,

– средняя скорость молекул вещества,

– средняя длина свободного пробега молекулы,

– молярная теплоемкость газа при постоянном объеме,

– число Авогадро,

– плотность вещества,

– удельная теплоемкость газа при постоянном объеме,

– масса молекулы.

Теперь рассмотрим, от каких факторов зависит и, следовательно, от каких не зависит коэффициент теплопроводности газов.

Поскольку для всех молекул примерно одинаковы, и значения мало отличаются для различных газов, главное изменение теплопроводности при фиксированной концентрации частиц газа происходит из-за различия в средней скорости теплового движения молекул:

, (17)

где – средняя скорость молекулы;

– постоянная Больцмана;

– температура вещества;

– масса молекулы.

Из формул (16) и (17) следует, что коэффициент теплопроводности газов обратно пропорционален (у легких газов коэффициент теплопроводности больше, чем у тяжелых) и прямо пропорционален . В действительности же коэффициент теплопроводности, как показывает опыт, растет с температурой несколько быстрее, чем . Это объясняется тем, что коэффициент теплопроводности прямо пропорционален еще и средней длине свободного пробега, а эта величина тоже растет с температурой. Для многоатомных газов необходимо еще учесть возрастание теплоемкости с температурой.

Из входящих в (16) величин только число молекул в единице объема и длина свободного пробега зависят от давления. Но прямо пропорционально давлению газа (), а обратно пропорциональна давлению газа, так как средняя длина свободного пробега молекулы газа

, (18)

где – эффективный диаметр молекулы,

– концентрация молекул.

Следовательно, коэффициент теплопроводности газов не зависит от давления (исключение составляет случай малых давлений).

Установим связь коэффициента теплопроводности с другими коэффициентами, характеризующими процессы переноса.

Известно, что коэффициент динамической вязкости равен

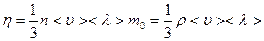, (19)

где – концентрация молекул вещества,

– средняя скорость молекул вещества,

– средняя длина свободного пробега молекулы,

– масса молекулы,

– плотность вещества.

А коэффициент диффузии равен

, (20)

где – средняя скорость молекул вещества,

– средняя длина свободного пробега молекулы.

Тогда из выражений (16), (19) и (20) следует, что

, (21)

и 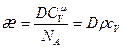, (22)

где – коэффициент теплопроводности,

– коэффициент динамической вязкости,

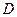– коэффициент диффузии,

– молярная теплоемкость газа при постоянном объеме,

– удельная теплоемкость газа при постоянном объеме,

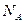– число Авогадро,

– масса молекулы,

– плотность вещества.

Наличие этой связи между коэффициентами процессов переноса обусловлено одинаковой физической природой процессов переноса и тем, что все они описываются одинаковыми уравнениями вида (8).

Дата добавления: 2015-07-11