Уравнение Фурье для теплопроводности газов

Теплопроводность – это процесс переноса теплоты из области с более высокой температурой в область, где она ниже, в результате теплового движения микрочастиц в среде. Таким образом, передача теплоты при теплопроводности приводит к выравниванию температуры среды.

Силы взаимодействия между молекулами газа не велики и, следовательно, не оказывают существенного влияния на их движение. Кроме того, молекулы газа проходят свободно без столкновений расстояние, соответствующее средней длине свободного пробега. Следовательно, теплопроводность в газах осуществляется передачей теплового движения от одних молекул другим в большей степени в результате перемещения молекул газа и в меньшей – в результате их взаимодействия друг с другом.

Предположим, что передача теплоты осуществляется исключительно путем теплообмена, что конвекции нет, и, что потерями теплоты на лучеиспускание можно пренебречь. Кроме того, будем предполагать, что объем системы остается постоянным, так что никаких перемещений вещества в процессе передачи теплоты не возникает. И сначала, для простоты, ограничимся рассмотрением одномерной задачи, когда температура среды, помимо времени, зависит только от одной пространственной координаты.

В этом случае (в случае теплопроводности) есть средняя энергия теплового движения, приходящаяся на одну молекулу. Она переменна в том случае, если от точки к точке меняется температура. При этом – поток теплоты, который входил в уравнение (9) и который далее будем обозначать .

Из теоремы о равнораспределении энергии по степени свободы имеем

, (11)

где – температура,

– число степеней свободы,

– постоянная Больцмана,

– число Авогадро,

– универсальная газовая постоянная,

– молярная теплоемкость газа при постоянном объеме.

Тогда подставляя это в уравнение переноса (8) получим

. (12)

То есть уравнение Фурье для теплопроводности газов

, (13)

где – плотность теплового потока (то есть количество теплоты, проходящее в единицу времени через единицу площади поверхности);

– коэффициент теплопроводности;

– частная производная температуры по .

Уравнение (13) можно обобщить на трехмерный случай:

, (14)

или в векторном виде:

, (15)

где – вектор плотности теплового потока;

– коэффициент теплопроводности;

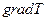– градиент температуры.

В уравнении Фурье для теплопроводности газов знак “–“ выражает направление переноса тепла от области с большей температурой к области с меньшей температурой, тогда как градиент направлен в сторону возрастания этой величины.

Дата добавления: 2015-07-11