Передача теплоты через плоскую стенку.

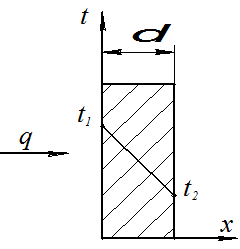Рассмотрим передачу теплоты через плоскую стенку (рис. 1.3) в случае, когда заданы граничные условия первого рода. Стенка толщиной δ имеет постоянный коэффициент теплопроводности λ. На наружных поверхностях стенки поддерживаются постоянные температуры t₁ и t₂. При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки. Направим ось х, как показано на рис. 1.3, тогда для осей y и z справедливо:

В связи с этим температура будет функцией только координаты х, а дифференциальное уравнение для этого случая будет иметь вид:

Граничные условия в рассматриваемой передаче запишем следующим образом:

при х = 0, t = t₁

при х = δ, t = t₂

Дифференциальное уравнение вместе с граничными условиями дают полную математическую формулировку поставленной задачи.

В результате решения этой задачи должно быть найдено распределение температуры в плоской стенке t = f(x), и получена формула для определения плотности теплового потока.

Закон распределения температуры в плоской стенке найдем выполнив интегрирование уравнения:

Таким образом, при постоянном коэффициенте теплопроводности, температура в стенке изменяется по линейному закону.

Константы определим из граничных условий:

при х = 0, t = t₁ => С₂ = t₁

при х = δ, t = t₂ =>

Для определения количества теплоты, проходящего через единицу поверхности стенки в единицу времени в направлении оси х, воспользуемся законом Фурье, согласно которому:

Учитывая, что

и , получим:

.

Из полученного уравнения следует, что количество теплоты, проходящее через единицу поверхности стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности λ и разности температур, и обратно пропорционально толщине стенке δ. Отметим, что тепловой поток определяется не абсолютным значением температур, а их разностью, которую называют температурным напором.

Отношение называется тепловой проводимостью стенки, а обратная величина – тепловым (термическим) сопротивлением стенки, которое представляет собой падение температуры в стенке на единицу плотности теплового потока.

Зная плотность теплового потока, легко вычислить общее количество теплоты Q, которое передается через стенку площадью F за промежуток времени τ:

Используя, полученные выражения, можем записать температурное поле в виде:

В действительности коэффициент теплопроводности λ является переменной величиной. Рассмотрим случай, когда коэффициент теплопроводности является функцией температуры λ = λ(t).

Для многих материалов зависимость коэффициента теплопроводности от температуры близка к линейной:

,

где 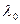– значение коэффициента теплопроводности при 0°С.

На основании закона Фурье, запишем:

Выполнив интегрирование , найдем среднеинтегральное значение коэффициента теплопроводности:

Тогда плотность теплового потока можно вычислить по формуле:

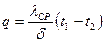
Таким образом, если коэффициент теплопроводности зависит от температуры, то для вычисления теплового потока можно использовать среднеинтегральное значение теплопроводности в заданном интервале температур.

Дата добавления: 2015-07-11