Передача теплоты от одной среды (жидкости или газа) к другой через разделяющую их стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости (газа) к стенке, теплопроводность в стенке и теплоотдачу от стенки к более холодной жидкости (газу).
Рассмотрим теплопередачу от одной жидкости к другой через однослойную плоскую стенку (рис. 1.3.2). Пусть плоская стенка имеет толщину δ. Заданы коэффициент теплопроводности стенки λ, температуры окружающих сред, а также коэффициенты теплоотдачи. Будем считать, что все эти величины не меняются вдоль поверхности. Это позволяет рассматривать изменение температур стенки и жидкости только в направлении, перпендикулярном плоскости стенки.
При заданных условиях необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхности стенки.
Плотность теплового потока от горячей жидкости к стенке определяется уравнением:
Та же плотность теплового потока, обусловленная теплопроводностью, определится как:
Та же плотность теплового потока от второй поверхности стенки к холодной жидкости за счет теплоотдачи:
Определив из этих выражений температурный напор и выполнив суммирование, получим:
Отсюда плотность теплового потока:
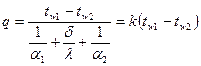
Величина k имеет такую же размерность, что и α 
, и называется коэффициентом теплопередачи. Коэффициент теплопередачи численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус.
Величина, обратная коэффициенту теплопередачи, называется термическим сопротивлением теплопередачи:
Термическое сопротивление теплопередачи складывается из термического сопротивления теплоотдачи от горячей жидкости к поверхности стенки, термического сопротивления теплопроводности стенки и термического сопротивления теплоотдачи от поверхности стенки к холодной жидкости.
Очевидно, что для многослойной стенки термическое сопротивление теплопередачи будет:
Тепловой поток Q, через поверхность стенки F равен:
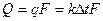
Температуры поверхности стенки можно найти из уравнений:
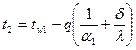
Дата добавления: 2015-07-11; просмотров: 61 | Нарушение авторских прав