Вычисление точечного бисериального ко­эффициента корреляции Пирсона

Примечание: 1 — совпадение с «клю­чом»; 0 — несовпадение с «ключом».

В отличие от других коэффициентов корреляции, r_bis может принимать значе­ния ниже -1 и выше +1. В случае попада­ния значения в эти области делается вы­вод о некорректности предположения о нормальном законе распределения X или о распределении значений X в выборке с эксцессом значительно ниже нормаль­ного. Следует обратить внимание на то обстоятельство, что при распределении переменных X с эксцессом больше нор­мального границы r_bis будут соответствен­но меньше пределов -1 и +1, что приве­дет к переоценке степени связи. Это требует тщательной проверки свойств распределения при использовании бисе­риального коэффициента корреляции.

При вычислении r_pb и r_bis оперируют одинаковыми исходными данными, однако эти коэффициенты не тождественны. Ко­эффициент r_pb более строг при характери­стике степени связи между X и Y (r_bis > r_pb). Случаи, когда одна из перемен­ных представлена в дихотомической шка­ле, а другая — в порядковой, требуют применения коэффициента рангово-бисериальной корреляции

где — средний ранг объектов, имею­щих 1 по X; 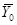— средний ранг объектов с 0 по X. Пример вычислений приведен в табл. 11. Коэффициент r_rb тесно связан с коэффициентом τ Кендалла. Особенно четко эта связь прослеживается при анализе корреляционной связи с помощью близкого к r_rb коэффициента r_pb в случае использования для его определения поня­тия совпадения и инверсии (см. Корреля­ция ранговая):

где n₀ — число объектов с нулевой дихотомией; п₁ — число объектов с еди­ничной дихотомией; Р — сумма совпаде­ний; Q — сумма инверсий.

Таблица 11

Вычисление рангово-бисериальной корреляции r_rb при сопоставлении результатов теста у девочек(1) и мальчиков(О)

При оценке значимости связи можно использовать критерий Стьюдента:

При количестве степеней свободы п' = п - 2 = 8t_кp = 2,306, при α = 0,05; t > t_кp, следовательно, при α < 0,05 выявленная связь является статистичес­ки значимой.

КОРРЕЛЯЦИЯ КАЧЕСТВЕННЫХ ПРИЗНАКОВ — метод анализа связи переменных, измеряемых в порядковых шкалах и шкалах наименований (см. Шкалы измерительные). Наиболее часто такой корреляционный анализ прово­дят с помощью коэффициентов корреля­ции ранговой, используемых в случаях, когда обе переменные измеряются в шка­лах порядка или легко могут быть преоб­разованы в ранги. При измерении сравни­ваемых переменных в шкалах наименова­ний широко применяются коэффициенты сопряженности, в которых в качестве про­межуточной расчетной величины исполь­зуется критерий согласия Пирсона (см. Критерий χ ²). Наиболее часто в таких расчетах пользуются коэффициентом со­пряженности Пирсона:

Значение Р всегда положительно и из­меряется от нуля до единицы. Особеннос­тью коэффициента сопряженности Пир­сона является то, что максимальное его значение всегда меньше +1 и в значительной степени зависит от количества на­блюдений (размера таблицы). В случае квадратной таблицы (k ´ k)

Так, в таблице размером (5 х 5) P_mах = = 0,894; в таблице (10 х 10) P_mах = 0,949. Поэтому окончательной формой выраже­ния связи между переменными с помо­щью коэффициента Пирсона является его отношение к величине Р_mах для данного случая (Р/Р_mах).

При расчете сопряженности находит применение также коэффициент Чупрова:

где t — число столбцов таблицы, k — чис­ло строк таблицы.

В психологической диагностике опи­санные коэффициенты используются от­носительно редко.

КОРРЕЛЯЦИЯ РАНГОВАЯ — метод корреляционного анализа, отражающий отношения переменных, упорядоченных по возрастанию их значения. Наиболее часто К. р. применяется для анализа свя­зи между признаками, измеряемыми в по­рядковых шкалах (см. Шкалы измери­тельные), а также как один из методов определения корреляции качественных признаков. Достоинством коэффициен­тов К. р. является возможность их ис­пользования независимо от характера распределения коррелирующих призна­ков.

В практике наиболее часто применя­ются такие ранговые меры связи, как ко­эффициенты К. р. Спирмена и Кендалла. Первым этапом расчета коэффициентов К. р. является ранжирование рядов переменных. Процедура ранжирования начи­нается с расположения переменных по возрастанию их значений. Разным значе­ниям присваиваются ранги, обозначае­мые натуральными числами. Если встречаются несколько равных по значению пе­ременных, им присваивается усреднен­ный ранг (табл. 12).

Таблица 12

Ранжирование распределения показателей теста (л = 18)

В табл. 13 приведены данные для рас­чета коэффициентов К. р. Во второй гра­фе представлены ранжированные пока­затели по первому из сравниваемых рас­пределений (оценка IQ, в третьей гра­фе — соответствующие им данные теста зрительной памяти).

Таблица 13

Дата добавления: 2015-07-10