Распределение IQ-оценок и показателей теста зрительной памяти

Коэффициент корреляции рангов Спирмена (r_s) определяется из уравне­ния:

где d_i — разности между рангами каждой переменной из пар значений X и Y; n — число сопоставляемых пар.

Используя данные табл. 12, получаем:

Коэффициент корреляции рангов Кендалла τ определяется следующей форму­лой:

где Р и Q рассчитываются по табл. 12. Так, в восьмой графе подсчитывается, на­чиная с первого объекта X, сколько раз его ранг по Y меньше, чем ранг объектов, рас­положенных ниже. Соответственно в девя­той графе (S₂) фиксируется, сколько раз ранг Y больше, чем ранги, стоящие ниже его в столбце X. Подставляя эти данные в формулу, получаем:

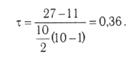
При сопоставлении приведенных ко­эффициентов оказывается, что коэффициент τ более информативен, чем r_s, и рас­считывается проще. Поэтому на практике при расчете К. р. отдают предпочтение ко­эффициенту τ.

КОСА КУБИКИ — невербальный тест интеллекта. Предложен К. Косом в 1920г.

Испытуемому предлагают составить фигуры из цветных кубиков по рисункам-образцам. Тестовый материал состоит из шестнадцати кубиков с ребром 2,5 см, сто­роны которых окрашены в красный, белый, желтый и синий цвета. Оставшиеся две противоположные грани разделены по диагонали, причем одна окрашена в белый и красный цвета, а вторая — в синий и желтый (см. Векслера интеллекта из­мерения шкалы, рис. 13). В набор вклю­чены восемнадцать образцов фигур, пер­вый из которых является тренировочным и выполняется совместно с испытуемым. Цвета рисунков-образцов соответствуют цветам кубиков, но размеры образцов вдвое меньше. Образцы размещены посе­редине картонной карточки, имеющей размер 10 х 7,5 см.

Задания следуют в порядке возраста­ющей трудности, что обеспечивается пос­ледовательной комбинацией следующих условий:

— фигуру можно построить только из од­ноцветных сторон кубиков;

— для построения фигуры следует ис­пользовать несколько двухцветных граней;

— фигуру можно сложить только из двухцветных сторон или из сочетания двухцветных и одноцветных, причем на образце не обозначена граница между соседними кубиками;

— образец повернут на 45°, т. е. стоит на ребре;

— для составления фигур требуется ис­пользовать все большее количество кубиков;

— образцы постепенно становятся все менее симметричными;

— увеличивается количество цветов на образце;

— образец не ограничивается рамкой, так что на краях сливается с фоном.

Образцы-рисунки испытуемому предъ­являются последовательно, тестирование прекращается после пяти последовавших друг за другом неудачных решений. Ус­пешность оценивается с нескольких позиций. Самым важным показателем явля­ется время решения отдельных заданий. В протоколе фиксируется и количество попыток при выполнении. Первичные оценки по результатам выполнения зада­ний переводятся в показатель умствен­ного возраста. В более поздних модифи­кациях оценки переводятся в IQ-показа-тели стандартные. Данные дополняют­ся качественным анализом поведения ис­пытуемого.

К. к. принадлежат к часто применяе­мым тестам и широко используются как в оригинальной, так и в сокращенных моди­фикациях (см., напр., Векслера интел­лекта измерения шкалы). Ценность те­ста определяется особенностями деятель­ности испытуемого, которая моделирует­ся его заданиями. Испытуемый начинает выполнение задания с анализа образца, путем сопоставления фрагментов образца с гранями кубиков. Затем осуществляет­ся генерализация выделяемого признака. Вслед за этим осуществляется переход к синтезу — констатация соответствия между образцом и собранной из кубиков фигурой. По мнению К. Коса, в ходе реше­ния заданий задействуются все мысли­тельные процессы.

Имеются сведения о валидности конструктной К. к. Получена значимая кор­реляция с Бине—Симона умственного развития шкалой (r =0,82 у нормаль­ных детей и r = 0,67 у слабоумных детей). Изучались связи показателей К. к. с основными тестами интеллекта, в частно­сти Станфорд—Бине умственного раз­вития шкалой (r = 0,77), Равена про­грессивными матрицами (r = 0,81). Об­ращается внимание на независимость друг от друга показателей К. к. и тестов арифметических способностей.

Наиболее широкое применение К. к. находят в клинической психодиагностике (В. М. Блейхер, И. В. Крук, 1986). По данным Л. Кошча (1976), тест весьма по­лезен при работе с такими разнообразны­ми контингентами испытуемых, как твор­ческие личности с высоким уровнем спо­собностей и, с другой стороны, умствен­но отсталые лица; дети с минимальной мозговой дисфункцией, нарушением концентрации внимания, нарушением про­странственной ориентировки; дети, стра­дающие неврозами; дети с задержкой психического развития, педагогически за­пущенные; больные юношеского и зрело­го возраста, страдающие шизофренией. Тест может использоваться и при анали­зе интеллектуального потенциала здоро­вых лиц.

В отечественной психодиагностике К. к. используются чаще всего в том виде, как они представлены в соответствующем отдельно взятом субтесте Векслера ин­теллекта измерения шкалы.

КОЭФФИЦИЕНТ АЛЬФА (α) — ста­тистический показатель, используемый при дисперсионном анализе. Предложен Л. Кронбахом (1971). Наиболее часто при­меняется при оценке надежности теста. Уравнение К. А. имеет следующий вид:

где п — количество заданий теста, — квадрат стандартного отклонения для все­го теста, — сумма квадратов стандартных отклонений для отдельных зада­ний. В том случае, если в методике применяются задания дихотомического типа («да»—«нет», «правильно»—«неправиль­но»), может быть использована упрощен­ная формула:

где и Р — доля испытуемых, давших «ключевой» или правильный от­вет, a Q = 1 - Р. Дихотомический вариант К. А. является уравнением Кьюдера—Ри­чардсона (см. Надежность частей тес­та). Применение К. А. основано на моде­ли, предполагающей наличие большой дисперсии (а стало быть, и дискриминативности заданий теста) скорее у надеж­ного, чем у ненадежного теста (см. Надежность факторно-дисперсионная). Таким образом, если при факторном анализе возвести в квадрат и просумми­ровать нагрузки выявленных факторов, можно определить надежность, поскольку нагрузки факторов представляют корре­ляцию теста с общими или специфически­ми факторами. Модель надежности фак­торно-дисперсионной близка к анализу надежности по внутренней согласо­ванности.

Факторно-дисперсионный метод ана­лиза надежности находится в сильной за­висимости от выбора переменных, в свя­зи с которыми факторизуется тест. Так, если сопоставлять тест математических способностей с личностными или мотивационными переменными, то оценка на­дежности была бы неадекватной (практи­чески не было бы общих факторов). С дру­гой стороны, если бы тест факторизировался совместно с тестами общих способ­ностей так, чтобы каждый тест мог нагру­жать соответствующие ему факторы, ме­тод надежности факторно-дисперсионной мог бы быть достаточно точным. Таким об­разом, эта модель подходит для оценки на­дежности теста, факторная валидность которого известна или задана при разра­ботке, а также тестов, связанных с огра­ниченным числом общих факторов.

КРИТЕРИАЛЬНО-КЛЮЧЕВОЙ ПРИНЦИП — принцип конструирова­ния тестов на основе обнаружения (эмпи­рического) психологических признаков, позволяющих дифференцировать релевантные критериальные группы от конт­рольных. Широко используется для кон­струирования психодиагностических ме­тодик наряду с факторно-аналитическим принципом. Примером методик, в кото­рых реализован К.-к. п., являются опрос­ники эмпирические, такие как Миннесотский многоаспектный личностный опросник, «Бланк интересов» Стронга (см. Опросники интересов) и др.

Так, при разработке MMPI из первона­чального банка утверждений в основные клинические шкалы включались только те, которые хорошо дифференцировали испытуемых с тем или иным клиническим диагнозом от контрольной группы здоро­вых людей (см. Дискриминативностъ заданий теста). В шкалы «Бланка инте­ресов» Стронга вошли те утверждения из первоначального набора, которые реально разделяли группы лиц, являвшихся носи­телями определенных интересов. Иногда задания, объединенные общей шкалой в силу эмпиричности конструирования, не имеют не только теоретического, но даже интуитивного, гипотетического объясне­ния.

В тех случаях, когда необходимо диск­риминировать группы, напр., в профотбо­ре, К.-к. п. является достаточно эффек­тивным.

В тестах, созданных в соответствии с К.-к. п., основное значение придается дискриминативности. Важен тот факт, что тест является дискриминативным, а не причина, по которой это происходит. В связи с использованием К.-к. п. конструи­рования тестов возникает ряд проблем, которые должен решать разработчик. К их числу в первую очередь следует отнести трудности в отборе критериальных групп. MMPI, например, разрабатывался, как указывалось выше, путем сопоставления больных и здоровых, однако разработка шкалы шизофрении (S_c) или паранойи (Р_а) с большим успехом могла бы опирать­ся на сопоставление группы больных с вы­раженными шизоидными или паранойяль­ными тенденциями с группой пациентов, у которых отмечаются противоположные патологические особенности, но это прак­тически нереально. Комплектование кри­териальной группы больных опиралось на врачебный диагноз, который разными спе­циалистами может восприниматься по-разному. Сложность в отборе «чистых» групп для сравнения ведет в конечном итоге к снижению надежности и валидности теста. (См. также Контрастные группы.)

Другая проблема связана со значи­тельными трудностями, а иногда и невоз­можностью психологической интерпрета­ции показателей тестов, созданных в соответствии с К.-к. п. Наиболее вероят­ным является то, что одна критериальная группа отличается от релевантной ей не одним, а несколькими (иногда многими) переменными. Полученные шкалы явля­ются, таким образом, не однозначными, а мультивариантными. Следовательно, два идентичных показателя могут иметь различную интерпретацию, и не существует определенного способа по виду показате­ля установить, что измеряет данная шка­ла. Факт, что тест может дискриминиро­вать группу X от группы Y, не говорит ничего о природе переменной, измеряе­мой тестом, если только мы не располага­ем доказательством, что группы отличаются одна от другой лишь по одной пере­менной.

Результатам тестов, разработанных на основе К.-к. п., присуща известная специ­фичность, что также является серьезным ограничением. Например, если такой тест используется для отбора сборщиков электронной аппаратуры, он будет разрабаты­ваться на основе конкретного критерия, связанного с выполнением работы опре­деленного характера. Если содержание работы изменится, разработанный на ос­нове неадекватных критериальных при­знаков тест станет бесполезен. В противо­вес этому тесты, ориентированные на ба­зовые способности, по-прежнему могут быть использованы.

Факторный тест, относительно «чис­тый» по исследуемым переменным и опирающийся на теорию измеряемого конструкта, как можно ожидать, будет предпочтительней страдающих эмпирич­ностью тестов, созданных в соответствии с К.-к. п. Однако разработка факторно-аналитического теста является техничес­ки более сложной, трудоемкой задачей.

Не нужно противопоставлять К.-к. п. конструирования тестов факторно-анали­тическому принципу; следует помнить, что при подборе первичного банка зада­ний разработчики исходят, как правило, из описания некоего свойства, конструк­та, являющегося объектом измерения. С другой стороны, разработанный по К.-к. п. тест в последующем может пройти проце­дуру факторизации.

«Эмпиричность» таких тестов в значи­тельной степени сглаживается и последу­ющей процедурой определения валидности конструктной.

Для методик, созданных в соответ­ствии с К.-к. п., наибольшее значение име­ют эмпирические модели определения на­дежности (см. Надежность ретестовая, Надежность параллельных форм, Надежность частей теста).

КРИТЕРИЙ χ² (критерий согласия Пир­сона) — характеристика распределения, используемая для проверки статистичес­ких гипотез. Под статистическим крите­рием подразумевается правило, обеспечивающее с определенной вероятностью принятие истинной или отклонение лож­ной гипотезы. В качестве критериев в математической статистике применяют определенные случайные величины, являющиеся функциями изучаемых случай­ных величин и чисел степеней свободы. Одним из наиболее часто применяе­мых является К. χ ², представляющий со­бой сумму квадратов отклонений эмпири­ческих частот (р) от теоретических или ожидаемых (р'), отнесенную к теоретиче­ским частотам:

При полном совпадении эмпирических и ожидаемых частот S (р - р') = 0. При несовпадении производится сравнение эмпирической величины χ ² с его крити­ческим значением, определенным по таб­лицам (см. Приложение III, табл. 3). Ну­левая гипотеза, которая предполагает, что расхождение между эмпирическими частотами и математическим ожиданием носит случайный характер и между вычисленными и эмпирическими частотами разницы нет, опровергается, если для принятого уровня значимости (α) и числа степеней свободы (df). В качестве примера проанализируем с помощью К. χ ² распределение частот выбора ответа на закрытый пункт теста (см. Задачи закры­того типа). Предлагаемые варианты не­правильных ответов должны быть при­мерно равновероятны. При обследовании 100 человек, отвечающих на проверяемый пункт неверно, результаты распредели­лись следующим образом (табл. 14).

Таблица 14

Дата добавления: 2015-07-10