Построение профиля кулачка для механизма с эксцентрично поставленным тарельчатым толкателем

При построении профиля кулачка данного вида из центра вращения кулачка О проводят окружность радиусом, равным смещению е. Если чертеж выполняется при условии равенства масштабов = , то радиус этой окружности равен (см. рис. 13). Для построения профиля кулачка сообщают кулачку угловую скорость ω. От прямой ОА противоположно направлению ω, откладывают фазовые углы φ₁, φ₂, φ₃ и φ₄.

Рис. 13 Построение профиля тарельчатого кулачкового механизма со смещением

Дуги, стягивающие фазовые углы φ₁ и φ₃, делят на столько же частей, на сколько разделена ось абсцисс диаграмм S=f(φ₁) и S=f(φ₃) (в нашем случае на 8). Через точки 0, 1, 2, 3,..., 17 проводят касательные к окружности с радиусом в сторону, противоположную угловой скорости кулачка. Если масштаб чертежа равен масштабу диаграммы перемещений (т.е. = ), то на касательных от точек 0, 1, 2, …, 17 откладывают отрезки, равные сумме минимального радиуса кулачка со смещением (см. пункт 5.1 и 5.2) и соответствующей ординаты диаграммы S=f(φ). Например, на касательной, проведенной к радиусу О-0 отложим отрезок , на касательной к радиусу О-1 – отрезок 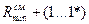и т.д. При этом получают точки 0*, 1*, 2*, …, 17*. Соединив эти точки плавной кривой, получим теоретический профиль кулачка на фазах подъема и опускания. На фазах дальнего и ближнего стояния профиль кулачка будет дугой окружности.

Для построения практического профиля через точки 0*, 1*, 2*... 17* проводим перпендикуляры к отрезкам 0-0*, 1-1*, 2-2*,... 17-17*. Практическим профилем кулачка будет внутренняя огибающая этих перпендикуляров.

ПРИМЕЧАНИЕ: Вышеперечисленные построения даны для случая равенства масштабов = . Если и не равны, то необходимо перед тем как откладывать величины ординат из диаграммы S=f(φ), привести их к масштабу , т.е. ординату измерить в миллиметрах, умножить на и разделить на .. Здесь масштаб чертежа, на котором вычерчивается профиль кулачка.

литература

1. И. И. Артоболевский "Теория механизмов и машин" М.-"Наука ", 1975.

2. С. Н. Кожевников "Теория механизмов и машин" М. - «Машиностроение», 1973.

3. А. С. Кореняко и др. "Курсовое проектирование по теории механизмов и машин", Киев, 1970.

Дата добавления: 2015-07-10