Косинусоидальный закон

График перемещений строят в координатах S=f(φ) (см. рисунок 3). По оси ординат откладывают отрезок h = 30...60 мм, соответствующий ходу толкателя S, тогда масштаб диаграммы перемещений определяем по формуле (5).

По оси абсцисс откладывают отрезки, соответствующие фазовым углам в принятом масштабе. Делят отрезки, φ₁.и φ₃ на 8 равных частей. Проводят полуокружность радиусом:

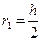. (9)

Полученную дугу делят на 8 равных частей, получаются точки 1, 2,... 8. Из точек деления проводят прямые, параллельные оси φ, на пересечении с соответствующими ординатами получаются точки 1*, 2*, … 8* и 9*, 10*,... 16*. Соединив их плавной кривой, получим график S = f(φ).

График 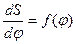строится следующим образом. Определяют радиусы окружностей:

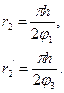(10)

Из начала координат радиусом r₂ проводят четверть окружности, которую делят на 4 равные части. Из точек деления проводят прямые, параллельные оси абсцисс, до пересечения с соответствующими ординатами.

Для фазы возвращения построения аналогичные, радиус r′₂.

График строят следующим образом. Определяют радиусы окружностей по формулам:

(11)

Из начала координат для фазы удаления и из точки 17 для фазы возвращения проводят полуокружности радиусами r₃ и r′₃. Делят эти полуокружности на 8 равных частей. Из точек деления проводят линии, параллельные оси абсцисс до пересечения с соответствующими ординатами. Точки пересечения соединяют плавными кривыми, которые являются косинусоидами.

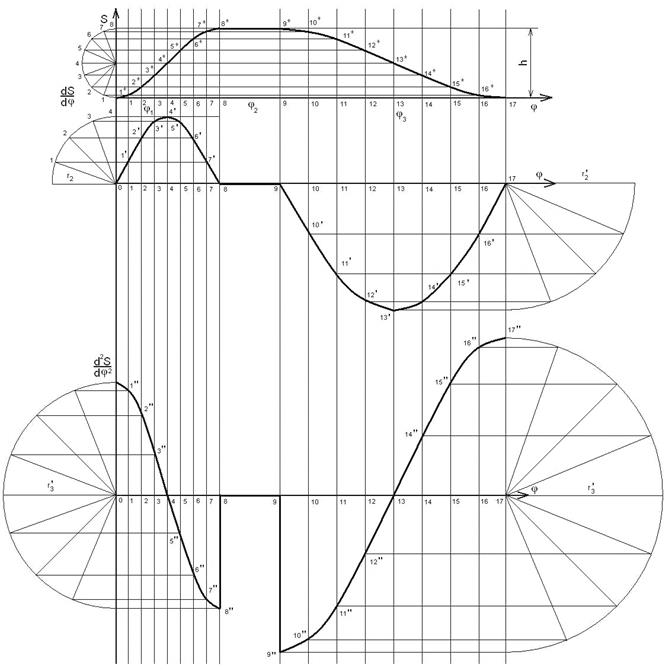
Рис. 3 Построение кинематических диаграмм для косинусоидального закона движения

Дата добавления: 2015-07-10