Читайте также:
|
| - уравнения двух пересекающихся прямых; | 
|
| - уравнения двух параллельных прямых; | 
|
| - уравнение двух совпадающих с осью ox прямых. |
| ПП 7.2. КРивые второго порядка | ||
| ПП 7.2. №1. | Найдите точки пересечения следующих линий:
1) (x – 1)2 + (y – 3)2 = 4 и(x – 3)2 + (y – 5)2 = 4;
2) (x – 5)2 + y 2 = 1и x + y = 0.
Решение:
1)  вычитая из первого уравнения второе,
получим систему 
решая которую, получаем две точки пересечения (1, 5) и (3, 3);
2)Линии (x – 5)2 + y 2 = 1 и x + y = 0 не пересекаются, так как система уравнений  не имеет действительных решений.
| 1) (1, 5) (3, 3).
2) 
|
| ПП 7.2. №2. | Составьте уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что малая ось равна 10, а эксцентриситет равен 12/13.
Решение:
Из условия имеем b = 5, е = 12/13. Поскольку е = с/а и а 2 = b 2 + c 2, то a 2 = b 2 + е 2 ×a 2 или  Подставляя числовые значения, получим
а 2 = 169.
Следовательно, уравнение эллипса имеет вид: 
| 
|
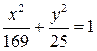
| ПП 7.2. №3. | Составьте уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что его большая ось равна 10, а расстояние между фокусами равно 8.
Решение:
Из условия имеем а = 5, с = 4. Вычислим малую полуось
Следовательно, уравнение эллипса имеет вид: 
| 
|
| ПП 7.2. №4. | Фокусы гиперболы совпадают с фокусами эллипса  Составьте уравнение гиперболы, если ее эксцентриситет равен 2.
Решение:
Из уравнения эллипса находим: a эл.2 = 25, b эл.2 = 9.
с эл.2 = a эл.2 - b эл.2 = 16, с эл. = 4.
По условию с гип. = с эл. = с и е гип. = с/а гип. = 2.
Таким образом, а гип. = с /2 = 2 и b гип.2 = с 2 – а гип.2 = 16 – 4 = 12.
Уравнение искомой гиперболы имеет вид: 
| 
|
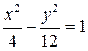
| ПП 7.2. №5. | Составьте уравнение параболы, если известны ее фокус F (-7, 0) и уравнение директрисы x – 7 = 0.
Решение:
Из уравнения директрисы имеем x = - p /2 = 7 или p = -14.
Таким образом, уравнение искомой параболы имеет вид y 2 = -28 x.
| y 2 = -28 x |
| ПП 7.2. №6. | Установите, какую линию определяет уравнение  Нарисуйте ее график.
Решение:
При  возведем обе части уравнения  в квадрат:
 или 
Выделяем в правой части полный квадрат:  или
Это уравнение гиперболы,. О¢ (3, 7), полуоси а = 2, b = 3.
Исходное уравнение  определяет нижнюю ветвь гиперболы, расположенную под прямой y= 7.
| Нижняя ветвь гиперболы |
| ПП 7.2. №7. | Установите, какую линию определяет уравнение  Нарисуйте ее график.
Решение:
Область допустимых значений (х, у) определяется условиями
(y + 1)/2 = 4×(1 – x)2 ® y + 1 = 8×(1 – x)2.
Искомая кривая – часть параболы с вершиной в точке (1, -1).
| Часть параболы |
| ПП 7.2. №8. | Установите, какую линию определяет уравнение  Нарисуйте ее график.
Решение:
Искомая кривая – часть окружности:
(y + 2)2 + (x – 4)2 = 52, y £ -2, x Î[-1, 9].
| Часть окружности |
| ПП 7.2. №9. | Установите, какую линию определяет уравнение y 2 – x2 = 0. Нарисуйте ее график.
Решение:
(y – x)×(y + x) = 0 – две пересекающиеся прямые.
| Две прямые |
| ПП 7.2. №10. | Какую линию определяет уравнение
x 2 + y 2 = x?
Решение:
Запишем уравнение в виде x 2 – x + y 2 = 0.
Выделим полный квадрат из слагаемых, содержащих х:
x 2 – x = (x – 1/2)2 – 1/4.
Уравнение принимает вид 
и определяет окружность с центром в точке (1/2, 0) и радиусом 1/2.
| Окружность |
Дата добавления: 2015-07-10; просмотров: 227 | Нарушение авторских прав