Проверка местной устойчивости стенки балки

Под действием нормальных и касательных напряжений стенка балки может потерять местную устойчивость, т.е. может произойти ее местное выпучивание. Это произойдет в том случае, если действующие в балке отдельные виды напряжений или их совместное воздействие превысят критические напряжения потери устойчивости. Устойчивость стенки обычно обеспечивают не за счет увеличения ее толщины, что привело бы к повышенному перерасходу материала из-за большого размера стенки, а за счет укрепления ее ребрами жесткости. Поперечные ребра устанавливаются так же в местах приложения больших сосредоточенных нагрузок и на опорах.

Стенку балки следует укреплять поперечными ребрами жесткости, если значение условной гибкости превышает 3,2 при отсутствии местной нагрузки на пояс балки и 2,2 – при наличии местной нагрузки.

Определяем условную гибкость стенки:

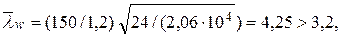
следовательно, поперечные ребра жесткости необходимы (рис. 5.7). Расстояние между основными поперечными ребрами a не должно превышать 2 h_w при `l<sub>w</sub> > 3,2 и 2,5 h<sub>w</sub> при `l_w £ 3,2. Для балок, рассчитываемых в упругой стадии, допускается превышать указанные выше расстояния между ребрами до значения 3 h_w при условии передачи нагрузки через сплошной жесткий настил или при значении гибкости сжатого пояса балкииз плоскости балки λ_f = l_ef / b_f, не превышающем ее предельного значения λ_fu (в примере это условие соблюдается: в середине пролета балки λ_f = 6,67< λ_fu = 15,64; в месте изменения сечения балки 12,56 < λ_fu = 14,3). При этом должна быть произведена проверка и обеспечена местная устойчивость элементов балки.

Рис. 5.7. Схема балки, укрепленной поперечными ребрами жесткости

Расстояние между ребрами назначаем , что увязывается с шагом балок настила Нельзя располагать ребра в местах монтажных стыков в балках, изготовленных из нескольких отправочных марок. При шаге а = 3 м поперечное ребро жесткости попадает на монтажный стык в середине пролета балки, поэтому первое и последующие за ним ребра смещаем к опоре на расстояние а /2 = 1,5м. Если стык поясов в месте изменения сечения балки по длине попадает на торец ребра, то стык несколько смещают в сторону к опоре.

Ширина выступающей части парного ребра должна быть не менее

b_r = h_w /30 + 40 = 1500 / 30 + 40 = 90 мм.

для одностороннего ребра – b_r = h_w / 24 + 50 = 1500 / 24 + 50 = 112,5 мм.

Толщина ребер

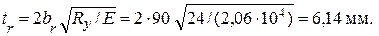
Принимаем ребро жесткости по ГОСТ 103–76* (табл. 5.2) из двух стальных полос 90´7 мм. Ребра жесткости привариваются к стенке непрерывными угловыми швами минимальной толщины. Торцы ребер должны иметь скосы с размерами 60´40 мм для снижения концентрации сварочных напряжений в зоне пересечения сварных швов и пропуска поясных швов балки.

Поперечное ребро жесткости, расположенное в месте приложения сосредоточенной нагрузки F_b = 334,08 кН к верхнему поясу балки проверяют расчетом на устойчивость: двустороннее ребро – как центрально-сжатую стойку, одностороннее – как стойку, сжатую с эксцентриситетом, равным расстоянию от срединной плоскости стенки до центра тяжести расчетного сечения стойки. При этом в расчетное сечение стойки включают сечение ребра жесткости и устойчивые полосы стенки шириной

c = 0,65 t_w = 0,65 · 1,2 = 22,85 см

с каждой стороны ребра, а расчетную длину принимают равной высоте стенки h_w = 1500 мм (рис. 5.8).

Рис. 5.8. Расчетное сечение условной стойки

Расчетная площадь стойки при двустороннем ребре

A_s = (2 b_r+ t_w) t_r+ 2 ct_w = (2 · 9 + 1,2) 0,7 + 2 ∙ 22,85 ∙ 1,2) = 68,28 см².

Момент инерции сечения стойки

I_z = t_r (2 b_r+ t_w)³/12 + 2c t_w ³/12 = 0,7 (2 ∙ 9 +1,2)³ / 12 + 2 ∙ 22,85 ∙ 1,2³ / 12 =

= 412,88 см⁴.

Радиус инерции

i_z = = = 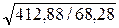2,46 см.

Гибкость стойки

λ_z = l_ef / i_z = 150 / 2,46 = 60,98.

Условная гибкость

Производим проверку устойчивости стойки:

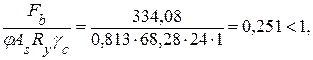
где φ = 0,813 – коэффициент устойчивости при центральном сжатии, принимаемый по табл. 6.1 в зависимости от условной гибкости λ_z для типа кривой устойчивости ^״ b ^״; тип кривой устойчивости зависит от формы сечений и толщины проката (см. табл. 5.10), при условной гибкости λ_z ≤ 0,4 коэффициент φ принимается равным единице.

Условие выполняется.

Устойчивость стенок балок не требуется проверять, если условная гибкость стенки _w не превышает значений:

3,5 – для балок с двухсторонними поясными швами при отсутствии местной нагрузки на пояс балки;

3,2 – для таких же балок с односторонними поясными швами;

2,5 – для балок с двухсторонними поясными швами при наличии местной нагрузки на пояс.

В нашем примере следовательно, требуется проверка стенки на местную устойчивость.

Расчет на устойчивость стенки балки симметричного сечения, укрепленной только поперечными основными ребрами жесткости, при отсутствии местных напряжений смятия 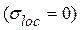и условной гибкости стенки выполняется по формуле

при наличии местного напряжения (см. рис. 17) – по формуле

где σ, t и σ_loc – действующие нормальные, касательные и локальные напряжения в месте соединения стенки с поясом от средних значений M, Q и F_b в пределах отсека; если длина отсека больше его расчетной высоты (a > h_w), то M и Q определяются для наиболее напряженного участка отсека с длиной, равной высоте отсека h_w; если в пределах отсека M и Q меняют знак, то их средние значения следует вычислять на участке отсека с одним знаком;

σ_сr, σ_loc,сr, τ_сr – критические напряжения, определяемые по СНиП [4].

Проверку местной устойчивости стенки производят в наиболее нагруженных отсеках: первом от опоры; среднем и, при наличии изменения сечения балки по длине, в отсеке с измененным сечением. В курсовой работе достаточно проверить стенку на устойчивость только в отсеке с измененным сечением балки.

Проверка местной устойчивости стенки в среднем отсеке балки (рис. 5.9).

Рис. 5.9. Распределение изгибающих моментов и поперечных сил

в среднем отсеке

Так как а = 3 м > h_w = 1,5 м, определяем M_ср и Q_ср по середине условного отсека шириной, равной половине высоты стенки h_w, для чего вычисляем величины моментов и поперечных сил на границах расчетного участка (х ₁ = 7,5 м; х ₂ = 9 м):

M ₁ = qx ₁(l – x ₁)/2 = 115,03 · 7,5 (18 – 7,5) / 2 = 4529,31 кН∙м;

M ₂ = M _max = 4658,72 кН∙м;

Q ₂ = 0;

M_ср = (M ₁ + M ₂)/2 = (4529,31 + 4658,72) / 2 = 4594,02 кН·м;

Q_ср = (Q ₁ + Q ₂)/2 = 172,55 / 2 = 86,28 кН.

Краевое напряжение сжатия в стенке

σ = M_ср (h_w / h)/ W_x = 4594,02 (150 / 155) /21234 = 20,09 кН/см².

Среднее касательное напряжение в отсеке

τ = Q_ср /(h_wt_w) = 86,28 / (150 ∙ 1,2) = 0,48 кН/см².

Локальное напряжение σ_loc = 0.

Критическое нормальное напряжение

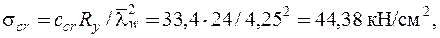
где c_сr = 33,4 – коэффициент, определяемый по табл. 5.6 в зависимости от значения коэффициента δ, учитывающего степень упругого защемления стенки в поясах:

здесь β = ∞ – при непрерывном опирании плит;

β = 0,8 – в прочих случаях.

Таблица 5.6

Значения коэффициента с_сr в зависимости от значения δ

d	£ 0,8	1,0	2,0	4,0	6,0	10,0	³30
ссr	30,0	31,5	33,3	34,6	34,8	35,1	35,5

Критическое касательное напряжение определяется по формуле

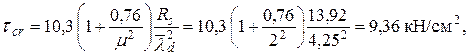
где 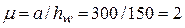– отношение большей стороны отсека a или h_w к меньшей d;

здесь d = h_w = 1,5 м < a = 3 м.

Проверяем местную устойчивость стенки:

Устойчивость стенки в середине балки обеспечена.

Проверка местной устойчивости стенки в месте изменения сечения балки на расстоянии х = 3 м от опоры.

Расчетные усилия

М ₁ = 2588,18 кН·м; Q ₁ = 690,18 кН.

Краевое напряжение сжатия в стенке

σ = M ₁(h_w / h)/ W ₁ = 258818 (150 / 155) /13357 = 18,75 кН/см².

Среднее касательное напряжение в отсеке

τ = Q ₁/(h_wt_w) = 690,18 / (150 ∙ 1,2) = 3,83 кН/см².

Локальное напряжение σ_loc = 0.

Критическое нормальное напряжение

где c_сr = 31,8 – по табл. 5.6 в зависимости от

Критическое касательное напряжение (см. проверку местной устойчивости стенки в среднем отсеке).

Производим проверку:

Стенка в отсеке балки с измененным сечением устойчива.

Проверка местной устойчивости стенки в первом отсеке в сечении на расстоянии от опоры x ₁ = a ₁/2 = 1,5 / 2 = 0,75 м (рис. 5.10),

здесь a ₁= h_w = 1,5 м.

Определяем усилия:

M ₁ = qx ₁(l – x ₁)/2 = 115,03 · 0,75 (18 – 0,75) / 2 = 744,1 кН∙м;

Краевое напряжение сжатия в стенке

σ = M ₁(h_w / h)/ W ₁ = 74410 (150 / 155) /13357 = 5,39 кН/см².

Среднее касательное напряжение в отсеке

τ = Q ₁/(h_wt_w) = 949 / (150 ∙ 1,2) = 5,27 кН/см².

Локальное напряжение

Критическое нормальное напряжение

при d = 1,16.

Рис. 5.10. К проверке местной устойчивости стенки балки у опоры

Критическое касательное напряжение определяется по формуле

где – отношение большей стороны отсека a или h_w к меньшей d;

здесь d = h_w = a ₁ = 1,5 м – меньшая из сторон отсека.

Производим проверку:

Стенка в первом от опоры отсеке устойчива.

В случае невыполнения условия устойчивости стенки необходимо увеличить толщину стенки t_w или уменьшить расстояние между поперечными ребрами жесткости а и повторно произвести проверку ее устойчивости.

Дата добавления: 2015-07-10