Проверка местной устойчивости стенки балки при наличии

местных напряжений (σ_loc ¹ 0)

При наличии местных напряжений (только для варианта, в котором имеются местные напряжения) проверку стенки на местную устойчивость следует выполнять в зависимости от значения a / h_w, при этом значения M и Q определяют в одном сечении балки.

Значения критических напряжений определяются в предположении выпучивания стенки между ребрами жесткости при ее потере устойчивости по одной полуволне при частом расположении ребер (a / h_w £ 0,8) и при более редкой расстановке ребер жесткости (a / h_w > 0,8) – по одной или двум полуволнам.

Значения нормального и локального критических напряжений при

a / h_w £ 0,8 вычисляются:

– критическое нормальное напряжение σ_cr определяется так же, как и при отсутствии местных напряжений по формуле

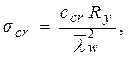
где c_cr определяется по табл. 5.6;

– критическое напряжение потери устойчивости от действия местных напряжений определяется по формуле

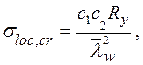
где с ₁ – коэффициент, принимаемый по табл. 5.7 в зависимости от a / h_w – соотношения сторон проверяемой пластины и значения ρ = 1,04 l_ef / h_w – относительной длины загружения пластины местной нагрузкой l_ef к высоте стенки h_w (см. рис. 5.4), здесь l_ef = b + 2 t_f;

с ₂ – коэффициент, принимаемый по табл. 5.8 в зависимости от отношения a / h_w и значения δ.

Таблица 5.7

Значение коэффициента c ₁

ρ	При a / hef или a 1/ hef, равном
≤0,50	0,60	0,67	0,80	1,0	1,2	1,4	1,6	1,8	≥2,0
0,10	56,7	46,6	41,8	34,9	28,5	24,5	21,7	19,5	17,7	16,2
0,15	38,9	31,3	27,9	23,0	18,6	16,2	14,6	13,6	12,7	12,0
0,20	33,9	26,7	23,5	19,2	15,4	13,3	12,1	11,3	10,7	10,2
0,25	30,6	24,9	20,3	16,2	12,9	11,1	10,0	9,4	9,0	8,7
0,30	28,9	21,6	18,5	14,5	11,3	9,6	8,7	8,1	7,8	7,6
0,35	28,0	20,6	18,1	13,4	10,2	8,6	7,7	7,2	6,9	6,7
0,40	27,4	20,0	16,8	12,7	9,5	7,9	7,0	6,6	6,3	6,1

Таблица 5.8

Значение коэффициента c ₂

d	При a / hef или a 1/ hef, равном
0,50	0,60	0,67	0,80	1,00	1,20	1,40	≥1,60
≤1	1,56	1,56	1,56	1,56	1,56	1,56	1,56	1,56
	1,64	1,64	1,64	1,67	1,76	1,82	1,84	1,85
	1,66	1,67	1,69	1,75	1,87	2,01	2,09	2,12
	1,67	1,68	1,70	1,77	1,92	2,08	2,19	2,26
	1,68	1,69	1,71	1,78	1,96	2,14	2,28	2,38
≥30	1,68	1,70	1,72	1,80	1,99	2,20	2,38	2,52

При отношении a / h_w > 0,8 рассматривают два случая проверки устойчивости стенки:

Первый случай. Вычисляют: – критическое нормальное напряжение σ_cr по формуле

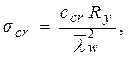
где c_cr определяется по табл. 5.6;

– критическое локальное напряжение потери устойчивости по формуле

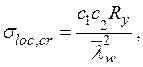
где для его вычисления при определении коэффициентов c ₁ и c ₂ по табл. 5.7 и 5.8 вместо a необходимо принять a ₁ = 0,5 a при0,8 ≤ a / h_w ≤ 1,33 и a ₁ = 0,67 h_w при a / h_w > 1,33.

Второй случай. Вычисляют: – критическое нормальное напряжение σ_cr по формуле

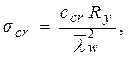
где c_cr определяется по табл. 5.9;

– критическое локальное напряжение потери устойчивости по формуле

где коэффициенты c ₁ и c ₂ определяют по фактическому отношению сторон a / h_w (если a / h_w > 2, в расчете принимают a / h_w = 2).

Таблица 5.9

Значения коэффициента c_cr в зависимости

от отношения a / h_w

a / hw	≤ 0,8	0,9	1,0	1,2	1,4	1,6	1,8	≥2,0
cсr	По табл. 19	37,0	39,2	45,2	52,8	62,0	72,6	84,7

Значение критического касательного напряжения τ_cr во всех случаях вычисляют по фактическим размерам отсека.

Проверка местной устойчивости стенки при наличии местных напряжений в среднем отсеке (в качестве примера).

При принятом шаге поперечных ребер жесткости а = 3 м отношение

Первая проверка. Локальное напряжение от сосредоточенной нагрузки s_loc = 13,58 кН/см².

Нормальное напряжение в среднем отсеке s = 20,9 кН/см².

Среднее касательное напряжение τ = 0,48 кН/см².

Значение критического нормального напряжения

44,38 кН/см²,

где c_cr = 33,4, определенное по табл. 5.6 при δ = 2,16.

Значение критического локального напряжения

где при вычислении коэффициентов с ₁ и с ₂ при a / h_w = 2 > 1,33 вместо а при-

нимаем а ₁ = 0,67 h_w = 0,67 ∙ 150 = 100,5 см, следовательно,

a ₁/ h_w = 100,5 / 150 = 0,67;

ρ = 1,04 l_ef / h_w = 1,04 ∙ 20,5 / 150 = 0,14

(здесь l_ef = b + 2 t_f = 15,5 + 2∙2,5 = 20,5 см – условная длина распределения сосредоточенной нагрузки);

с ₁ = 30,68 – коэффициент, определяемый по табл. 5.7 в зависимости от a ₁/ h_w = 0,67 и ρ = 0,14;

с ₂ = 1,64 – коэффициент, определяемый по табл. 5.8 в зависимости от a ₁/ h_w = 0,67 и δ = 2,16.

Значение критического касательного напряжения τ_cr = 9,36 кН/см².

Проверяем местную устойчивость стенки:

.

Стенка устойчива.

Вторая проверка. Значение критического нормального напряжения

где c_cr = 84,7 – коэффициент, определяемый по табл. 5.9 в зависимости от a / h_w = 300 / 150 = 2.

Значение критического локального напряжения

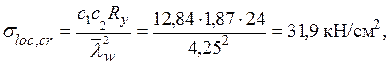
где с ₁ = 12,84 – коэффициент, определяемый по табл. 5.7 в зависимости от a ₁/ h_w = 2 и ρ = 0,14;

с ₂ = 1,87 – коэффициент, определяемый по табл. 5.8 в зависимости от a / h_w = 2 и δ = 2,16.

Значение критического касательного напряжения τ_cr = 9,36 кН/см².

Проверяем местную устойчивость стенки:

.

Стенка устойчива.

В балках большой высоты (h > 2 м ) с тонкой стенкой при условной гибкости _w > 5,5 для обеспечения ее устойчивости рационально, помимо поперечных ребер жесткости, ставить продольные ребра, опирающиеся на поперечные и располагаемые на расстоянии (0,2 – 0,3) h_w от сжатой кромки отсека. Наличие продольного ребра разбивает стенку по высоте на верхнюю и нижнюю пластинки, устойчивость которых проверяется раздельно по СНиП [4].

Дата добавления: 2015-07-10