Растворов электролитов

В растворах электролитов перенос электричества осуществляется за счет перемещения ионов. Для количественной характеристики способности растворов проводить электрический ток при приложении электрического напряжения используется электрическая проводимость (удельная и молярная).

Удельная электрическая проводимость раствора электролита – это электрическая проводимость раствора, заключенного между двумя плоскими электродами, площадью 1 м² каждый, расположенными параллельно на расстоянии 1 м друг от друга. Требования к электродам (плоские, параллельно расположенные) вытекают из необходимости создания однородного электрического поля.

Удельная электрическая проводимость æ является величиной, обратной удельному электрическому сопротивлению r:

æ =

(2.1)

Удельное электрическое сопротивление r определяется из уравнения:

,

(2.2)

где R – электрическое сопротивление, Ом;

– расстояние между электродами, м;

S – эффективное поперечное сечение раствора электролита, заключенного между электродами, м².

Единица измерения удельного электрического сопротивления – Ом×м. Следовательно, удельная электрическая проводимость æ выражается в Ом^-1×м^-1 или в См/м (сименс на метр).

Экспериментальное определение электрической проводимости растворов основано на измерении сопротивления кондуктометрической ячейки с платиновыми электродами и исследуемым раствором. Для любой ячейки можно определить константу k, которая называется постоянной кондуктометрической ячейки, и рассчитать удельную электрическую проводимость раствора по уравнению:

,

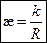(2.3)

где k – постоянная кондуктометрической ячейки, м^–1; R – измеренное сопротивление ячейки с раствором, Ом.

Постоянную кондуктометрической ячейки k выражают в м^-1 и определяют по раствору, удельная электрическая проводимость которого известна (обычно используют раствор хлорида калия).

Удельная электрическая проводимость зависит от переносимого каждым ионом заряда, концентрации ионов, скорости их перемещения (см. формулу (2.10)). Последнее затрудняет сравнение различных электролитов по их электрической проводимости. Поэтому чаще пользуются молярной электрической проводимостью.

Молярная электрическая проводимость l – это проводимость раствора электролита, содержащего 1 моль растворенного вещества и находящегося между двумя плоскими электродами, расположенными параллельно на расстоянии 1 м друг от друга.

Молярная и удельная электрические проводимости связаны между собой уравнением:

l =

(2.4)

где c – молярная концентрация электролита, моль/м³.

Молярную электрическую проводимость измеряют в

Ом^-1×м²×моль^-1 или См×м²/моль.

Такую величину как эквивалентная электрическая проводимость в настоящее время применять не рекомендуется.

Молярная электрическая проводимость возрастает с уменьшением концентрации раствора электролита, достигая максимального значения l_¥ при ¥ разбавлении. Поскольку в предельно разбавленном растворе взаимодействие между ионами отсутствует, можно считать, что каждый ион движется независимо от других ионов и, следовательно, с максимальной скоростью.

В условиях предельного разбавления электролитов выполняется закон Кольрауша:

,

(2.5)

где 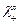и – молярные электрические проводимости соответственно катиона и аниона при бесконечном разбавлении.

Перемещение иона в электрическом поле характеризуют величиной электрической подвижности u_i, равной скорости движения иона в электрическом поле υ_i, деленной на напряженность этого электрического поля E:

ui = υi / E

(2.6)

Если скорость движения иона υ_i выражается в м/с, а напряженность электрического поля E – в В/м, то единицей измерения электрической подвижности u_i будет м²/(В×с).

Другой величиной, часто используемой при рассмотрении растворов электролитов, является число переноса t, представляющее собой долю общего количества электричества, переносимую ионами данного вида:

,

(2.7)

где q_i – количество электричества, переносимого i -ми ионами, Кл;

q – количество электричества, переносимого всеми ионами, Кл.

Числа переноса ионов связаны с электрическими подвижностями ионов следующими соотношениями:

,

(2.8.1)

,

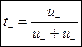(2.8.2)

где u₊ и u_– – электрические подвижности катиона и аниона соответ­ственно; t₊ и t_– – числа переноса соответственно катиона и аниона.

Алгебраическое суммирование уравнений (2.8.1) и (2.8.2) дает следующую очевидную формулу:

(2.9)

Связь между удельной электрической проводимостью æ и электрическими подвижностями ионов u_i выражается уравнением:

,

(2.10)

где F = 96485 Кл/моль – постоянная Фарадея;

z_i – зарядовое число иона i -го вида;

с_i – молярная концентрация i -х ионов, моль/м³;

u_i – электрическая подвижность i -го иона, м²/(В×с);

α – степень диссоциации электролита;

c – молярная концентрация электролита, моль/м³;

n_i – число ионов i -го вида в формульной единице электролита.

Для слабых электролитов используется понятие степени диссоциации a. При диссоциации слабого 1,1-зарядного электролита:

КА К⁺ + А^–

степень диссоциации a определяется формулой:

,

(2.11)

где [К⁺] и [А^–] – равновесная молярная концентрация катионов и анионов соответственно, моль/л; с – молярная концентрация электролита, моль/л.

Константа диссоциации К_дис электролита КА выражается по закону действующих масс уравнением:

,

(2.12)

где [КА] – равновесная молярная концентрация недиссоциированных молекул электролита, моль/л.

Выразим молярные концентрации ионов К⁺ и А^– и недиссоциированных молекул КА через степень диссоциации a, используя формулу (2.11) и уравнение материального баланса (2.15):

[К^+] = aс,

(2.13)

[А^–] = aс,

(2.14)

[КА] = с-aс = (1-a)×с

(2.15)

Подставив выражения (2.13) – (2.15) в уравнение (2.12), получим закон разведения Оствальда:

(2.16)

Степень диссоциации a слабого электролита в разбавленном растворе можно также выразить через молярную электрическую проводимость l:

,

(2.17)

где l – молярная электрическая проводимость при данной концентрации, См×м²/моль; l_¥ – молярная электрическая проводимость при бесконечном разведении, См×м²/моль.

Подстановка выражения (2.17) в уравнение (2.16) приводит к следующему соотношению:

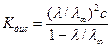
(2.18)

Используя формулу (2.4), приведем выражение (2.18) к следующему виду:

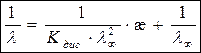
(2.19)

Уравнение (2.19) используется для определения К_дис и l_¥ по экспериментальным данным о зависимости электропроводности от концентрации электролита. При этом К_дис определяется по тангенсу угла наклона прямой, построенной в координатах , к оси абсцисс, а l_¥ находят по величине отрезка, отсекаемого данной прямой на оси ординат.

Задание 2

Определите графически константу кислотности К_к слабой кислоты по данным о зависимости электрического сопротивления ее водных растворов от разведения V при 25 °С, представленным в табл.2. Постоянная кондуктометрической ячейки k = 50 м^–1.

Таблица 2. Исходные данные к заданию 2.

№ вар	Кислота	Формула	Электрическое сопротивление R, Ом, при разведении V, л/моль
	Синильная	HCN
	Азотистая	HNO2
	Фторо-водородная	HF
	Йодная	HIO4
	Муравьиная	HCOOH
	Уксусная	CH3COOH
	Пропионовая	C2H5COOH
	Масляная	C3H7COOH
	Изомасляная	C3H7COOH
	Валериановая	C4H9COOH
	Фторуксусная	CH2FCOOH
	Хлоруксусная	CH2ClCOOH
	Дихлор-уксусная	CHCl2COOH
	Трихлор-уксусная	CCl3COOH
	Йодуксусная	CH2ICOOH
	Циан-уксусная	CH2CNCOOH
	Фенил-уксусная	C6H5CH2CO-OH
	Бензойная	C6H5COOH
	Салициловая	HOC6H4CO-OH
	Пикриновая	(NO2)3C6H2-OH
	Синильная	HCN
	Азотистая	HNO2
	Фторо-водородная	HF
	Йодная	HIO4
	Пропионовая	C2H5COOH
	Масляная	C3H7COOH
	Изомасляная	C3H7COOH
	Валериановая	C4H9COOH

Рассмотрим решение задания 2 на примере.

Пример 2

Для водных растворов слабой одноосновной кислоты в кондуктометрической ячейке с постоянной k = 35 м^-1 была получена следующая зависимость электрического сопротивления R раствора от разведения V:

Разведение V, л/моль
Сопротивление R, Ом

Определите константу диссоциации кислоты.

Для решения задачи удобно воспользоваться уравнением (2.19):

Удельную æ и молярную l электрические проводимости рассчитаем по формулам (2.3) и (2.4) соответственно:

æ = , l =

Результаты расчетов сведем в таблицу:

№ п/п	V, л/моль	R, Ом	æ, См/м
			9,75∙10^-2	3,12∙10^-3	320,54
			6,74∙10^-2	4,32∙10^-3	231,70
			4,62∙10^-2	5,92∙10^-3	168,97
			3,15∙10^-2	8,06∙10^-3	124,00
			2,13∙10^-2	1,09∙10^-2	91,91
			1,40∙10^-2	1,43∙10^-2	69,75

С целью определения К_к и l_¥ построим график в координатах (рис. 1). Как следует из уравнения (2.19), отрезок, отсекаемый прямой, изображенной на рис.1, на оси y, равен 1/ l_¥. Уравнение линии тренда на рис.1 позволяет найти l_¥:

1/ l_¥ = 28,721 Þ l_¥ = 3,48×10^-2 См×м²/моль.

Константу кислотности вычислим по формуле (2.20):

(2.20)

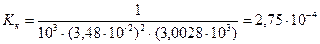моль/л.

Рис. 1. График для определения константы кислотности слабой кислоты.

Дата добавления: 2015-07-10