Рациональные уравнения

Два математических выражения, соединенные знаком равенства (=), образуют равенство. Если это числовое равенство, оно может быть истинным или ложным. Например, 9+16=25 - истинное равенство, а 7=8 - ложное. Если равенство содержит величины, обозначенные буквами, то оно может быть истинным при одних допустимых значениях, входящих в него букв, и ложным - при других. Если равенство является истинным при всех допустимых значениях, входящих в него букв, оно называется тождеством. Например, равенство 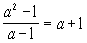есть тождество при всех .

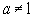Если же равенство, содержащее переменную величину, (которую обычно обозначают одной из последних букв латинского алфавита, например x) является истинным не при всех допустимых значениях этой переменной, оно называется уравнением (с одним неизвестным). Например, равенство 2 х +1=3 является уравнением. Оно истинно лишь при одном значении х =1.

Решением, или корнем уравнения, называется всякое значение неизвестного х, при подстановке которого в обе части уравнения получается истинное числовое равенство. Решить уравнение - значит найти все его корни или доказать, что корней нет. Областью допустимых значений (для краткости ОДЗ) уравнения называется множество всех значений неизвестного х, при которых математические выражения, входящие в обе части уравнения, имеют смысл, (т.е. все те значения х, при которых можно выполнить действия, указанные в этих выражениях).

Решая уравнение, мы применяем к нему некоторые преобразования: упрощаем выражения, входящие в уравнение, переносим слагаемые из одной части равенства в другую, умножаем или делим обе части уравнения на выражение, содержащее х, возводим обе части уравнения в степень, логарифмируем и т.п., т.е. так или иначе, заменяем исходное уравнение другим. Если исходное и преобразованное уравнения имеют одни и те же корни, то они называются равносильными. В частности, уравнения, которые не имеют корней, также считаются равносильными.

Два основных свойства уравнений:

1. Если какой-либо член уравнения перенести из одной части равенства в другую, сменив его знак на противоположный, то получится уравнение равносильное исходному.

2. Если обе части уравнения умножить или разделить на одно и то же не равное нулю число (или даже выражение, содержащее х, которое в ОДЗ не обращается в ноль), то новое уравнение будет равносильно исходному.

Конечно, при решении уравнений лучше всего каждый раз переходить к равносильному. Однако это удается далеко не всегда. Если все корни первого уравнения являются корнями второго, то второе уравнение называется следствием первого.

Если в результате преобразований мы заменим исходное уравнение следствием, то при решении нового уравнения мы можем получить корни, не являющиеся корнями исходного уравнения, т.е. посторонние корни. Однако, это не страшно, так как от посторонних корней, как правило, можно легко избавиться с помощью проверки.

Таким образом, при решении уравнений мы должны, в первую очередь, следить за тем, чтобы в результате преобразований исходного уравнения не происходила потеря корней, т.е. чтобы новое уравнение было следствием исходного или равносильно ему.

Если выражения, стоящие в левой и правой частях уравнения, составлены лишь с помощью операций сложения, вычитания, умножения, деления и возведения в целую степень, то уравнение называется рациональным. Рациональное уравнение называется целым, или алгебраическим, если в нем нет деления на выражение, содержащее х. К целым уравнением относятся, например, линейные и квадратные уравнения. Если в рациональном уравнении есть деление на выражение, содержащее х, то уравнение называется дробно-рациональным.

2.7 Метод интервалов решения неравенств.

Решение неравенств методом интервалов

Метод интервалов часто используют при решении Неравенств. Он позволяет свести решение неравенства вида h(x) > 0 (<, ≥,≤) к решению уравнения h(x) = 0.
Данный метод заключается в следующем:

1. Находится ОДЗ неравенства.

2. Неравенство приводится к виду h(x) > 0(<, ≥,≤) путем упрощения.

3. Решается уравнение h(x) = 0.

4. Если на ОДЗ отмечены точки, они ограничивают его и разбивают на интервалы знакопостоянства, при этом знак функции h(х) определяется на каждом таком интервале.

5. Решением является объединение отдельных множеств, на которых h(x) имеет соответствующий знак. После дополнительной проверки точки ОДЗ, являющиеся граничными, включаются (или не включаются) в ответ.

Метод интервалов основывается на том, что непрерывная функция h(x) меняет знак либо в граничных точках «разрыва» на ОДЗ, либо при переходе через 0, т.е. в тех точках, которые являются корнями уравнения h(x) = 0. В других точках перемены знака не происходит.
Пример:
Решить неравенство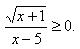
Решение:
ОДЗ: 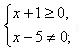откуда имеем x 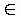[-1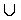; 5) (5; + )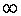
Решим уравнение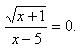
Числитель дроби равен 0 при x = -1, это и есть корень уравнения. Отметим найденный корень на числовой прямой (черным кружком, т.к. неравенство нестрогое), предварительно отметив ОДЗ:

Чтобы определить знак на промежутке (-1; 5) возьмем число 0,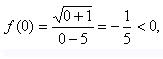
Чтобы определить знак на втором промежутке возьмем число 8,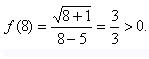
Точки 0 и 8 выбирались произвольно, но так, чтобы упростить процесс вычисления каждого значения функции.
Ответ: (-5; + ).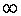

Дата добавления: 2015-07-12