Триграммный код

Арифмосемиотическая сторона учения о 12-ти люй более всего проступает в контексте теории триграмм. Как уже указывалось (см. рис. 2.6.6), на базис-схеме с триграммами в порядке “взаимопорождения” музыкальный звукоряд в целом образует интервал октавы с малой секундой, что составляет 6,5 тонов. Важно подчеркнуть, что при этом триграммы можно рассматривать не просто символами соответствующих ступеней, а их кодами со структурой, определяющей величину кодируемой ступени.

Для кодирования должны быть использованы интервалы квинты, большой терции и секунды. Квинта является интервалом, на основе которого строится звукоряд из 12-ти люй. Секунда образуется в результате сочетания двух квинт, сведенных в одну октаву. Что касается большой терции, то о знакомстве с ней древних китайцев можно судить по названиям нот системы люй. Если не считать ноты хуан чжун, то остальные три ноты, в названия которых входит иероглиф чжун (“колокол”), находятся друг от друга на интервалах, равных большой терции. То же самое относится и к трем нотам, в названия которых входит иероглиф люй (“флейта”) (см. табл. 2.6.1).

Итак, если позициям X, Y, Z поставить в соответствие интервалы квинты (3,5 тона), большой терции (2 тона) и секунды (1 тон), обозначаемые янскими знаками (1), то для каждой триграммы сумма янских знаков будет соответствовать количеству тонов, на которое ступень, символизируемая этой триграммой, отличается от ступени, символизируемой принятой за точку отсчета триграммой Кунь (000). Подобную кодировку можно применить и для иньских знаков (0), взяв за начало отсчета триграмму Цянь (табл. 2.6.3).

X. Квинта — 3,5 тона;

Y. Б. терция — 2 тона;

Z. Секунда — 1 тона.

Таблица 2.6.3
Код	Янский интервал от 000 (в тонах)	Иньский интервал от 111 (в тонах)	Нота
	3,5 + 2 + 1 = 6,5		c
	3,5 + 2 = 5,5		d
	3,5 + 1 = 4,5		e
	3,5	2 + 1 = 3	fis
	2 + 1 = 3	3,5	g
		3,5 + 1 = 4,5	a
		3,5 + 2 = 5,5	h
		3,5 + 2 + 1 = 6,5	cis

Выделенные квинтовым ходом ступени с “младшими” триграммами совпадают с эннеаграммными (точнее, додекаграммными) узловыми точками, на которых строится гексанема с “ротационным” (G) порядком. В додекаграмме, как указывалось выше (см. рис. 2.2.7), она объединяет числа, которые входят в периодическую дробь 12/7 = 1,[8|6|10|3|5|1], выраженную в двенадцатеричном счислении (рис. 2.6.7).

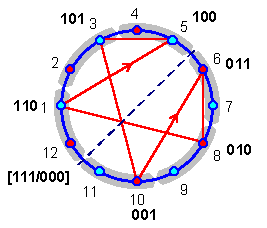
Рис. 2.6.7

Числовой порядок в данной фигуре сдвинут на одну единицу вперед относительно обозначения месяцев в китайском сельскохозяйственном календаре. Однако при выборе 12-ти частей круга для деления на число 7 нумерация этих частей будет совпадать с календарной.

Ранее было показано преобразование по гексанеме триграммных порядков (см. рис. 2.2.4; 2.2.9). В данном случае это преобразование можно конкретизировать привязкой к узловым точкам додекаграммы и ступеням звукоряда люй (рис. 2.6.8).

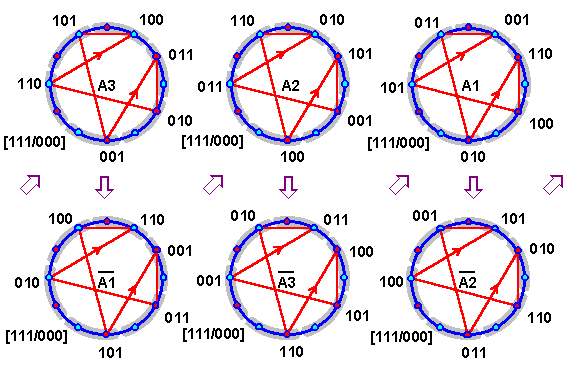
Рис. 2.6.8

Получившиеся порядки триграмм будут символизировать звукоряды с различными музыкальными интервалами — большими и малыми секундами, секстами, септимами, терциями и чистыми квинтами и квартами. Для наглядности все их можно изобразить на базис-схеме с круговым порядком “взаимопорождения” (А3), который сам является звукорядом с последовательностью шести больших и одной малой секунд (рис. 2.6.9).

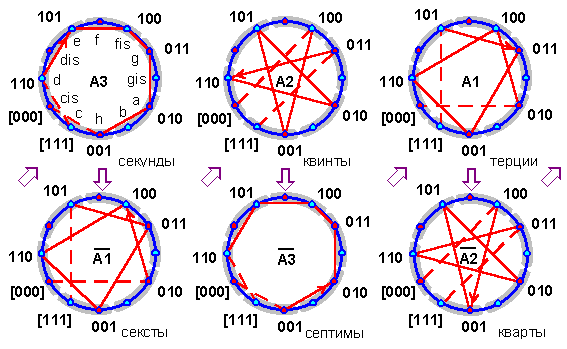
Рис. 2.6.9

Дата добавления: 2015-07-12