Семеричный цикл

Триграммы создавались как квазиуниверсальные символы и призваны символизировать различные циклы. Было показано, что на круговой схеме они могут символизировать шестеричный цикл за счет исключения “старших” триграмм и восьмеричный цикл за счет соотнесения со звукорядом, имеющим в случае порядка “взаимопорождения” диапазон в октаву с малой секундой. Триграммы также могут символизировать семеричный цикл, в котором, во-первых, триграмма Кунь (000) обозначает ту же самую фазу цикла, что и Цянь (111), но только на новом витке, и, во-вторых, сам цикл является октавным для порядка “взаимопорождения”. Получение других порядков в таком случае также может производиться с помощью перемещения символов триграмм по гексанеме. Кроме того, возможно еще преобразование порядков по семилучевой звезде, когда триграммы в порядке по звезде последовательно переставляются в порядок по кругу (рис. 2.6.10).

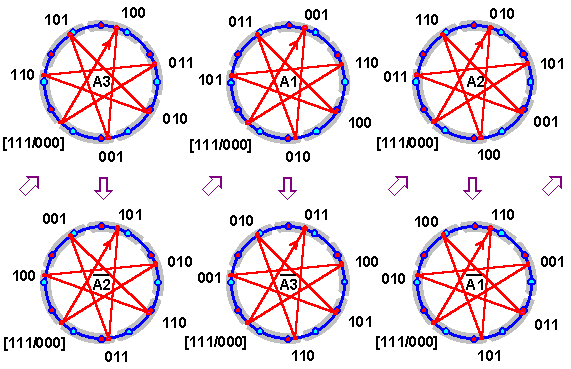
Рис. 2.6.10

Чтобы восемь триграмм укладывались таким образом в октавный круг, необходимо изменить кодировку их позиций следующим образом:

X. Условная квинта @ 1,486 < 3,5 тона;

Y. Условная б. терция @ 1,219 < 2 тона;

Z. Условная секунда @ 1,104 < 1 тона.

В темперированном строе 12 квинт составляют интервал в 7 октав, а в пифагоровом — чуть больший. Чистая квинта равна 3/2 = 1,5, а темперированная — приблизительно 1,498. Условная квинта образуется при делении круга на число 7, и 7 таких квинт составят 4 октавы.

Порядки А1, А2 и А3 можно представить в одной таблице (табл. 2.6.4), которая показывает принцип их преобразований, заключающийся в дихотомическом делении, подобном тому, что применяется при получении триграмм и гексаграмм из Великого предела. Этот принцип позволяет добавить в таблицу неограниченное количество столбцов справа и слева от имеющихся, что делает ее сходство со схемой Великого предела еще более очевидным.

Таблица 2.6.4
A2	A1	A3
000/111	000/111	000/111
		000/111
	000/111	000/111
		000/111
000/111	000/111	000/111

Другая аналогия, на которую здесь уместно указать, — это метод фракталов, или масштабного автоподобия. Взяв какой-либо триграммный порядок, через три шага преобразований можно получить тот же самый порядок, но масштабно уменьшенный или увеличенный. Так, если в качестве исходного берется порядок “взаимопорождения” (А3), который символизирует октаву, т.е. диапазон от 1 до 2, то этот же самый порядок при уменьшении будет символизировать диапазон от 1 до приблизительно 1,104, а при увеличении — от 1 до 128, что составляет точно 7 октав (табл. 2.6.5).

Таблица 2.6.5
A3	Уменьшение	Норма	Увеличение
			2^0 = 1
	1,014...	1,104...	2^1 = 2
	1,029...	1,218...	2^2 = 4
	1,043...	1,345...	2^3 = 8
	1,058...	1,485...	2^4 = 16
	1,073...	1,639...	2^5 = 32
	1,088...	1,810...	2^6 = 64
	1,104...		2^7 = 128

“ Порождающая” октава

“Порождающая” роль октавного диапазона заключается в том, что он, с точки зрения математической символики, является производным от единицы и производящим единицу. Можно сказать, что октавный переход от 1 к 2 (= 1 + 1) или от 1 к 1/2 (= ¹/_{1 + 1}) — это появление новой единичной сущности, копируемой по первичному эталону. Если полагать этот эталон вне сферы явлений, поскольку первоначально, будучи не сравним ни с чем, он как бы и не существует, то развитие октавы можно определить как становление бытия.

В музыке октава — установление наиболее консонансного звука, а с точки зрения психологии восприятия — появление нового качества, для которого задан прототип. В акустике октава рассматривается как удвоенное увеличение частоты, уменьшение периода колебаний некоего вибратора или уменьшение вдвое его длины. Иначе говоря, октава здесь рассматривается в категориях времени и пространства и представляет собой установление единиц их измерений.

Соотнесенность октавы с порядком “взаимопорождения” триграмм или стихий можно рассматривать в контексте древнекитайской картины мира как установление пространственно-временного континуума между Небом и Землей (см. табл. 2.3.9). Увеличивающийся по высоте вибраций поток энергии спускается от Неба к Земле, насыщая ее своей благодатной силой. Триграммы или стихии в порядке “взаимопорождения”, выраженные посредством музыкальных ступеней, — это как бы этапы такого нисхождения. Повышение частоты вибрации сопровождается понижением ее длины волны, поскольку между частотой и длиной волны имеется обратно пропорциональная зависимость, которую можно уподобить взаимоотношениям сил ян и инь, “являющихся корнями друг друга”. Музыкальный звукоряд люй прекрасно отражает этот дуализм (рис. 2.6.11).

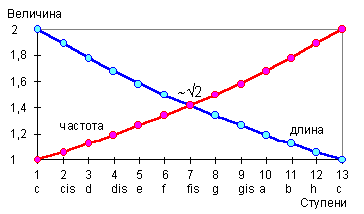
Рис. 2.6.11

Уравновешенность частоты и длины волны колебаний наблюдается на 7-й ступени, коррелирующей по реконструкции с хуан чжуном (см. рис. 2.6.6) и тем самым позволяющей еще раз утверждать о его срединности. В порядке “взаимопорождения” данный пункт совпадает с фазой кульминации описываемого этим порядком процесса, c окончанием действия триграммы Гэнь и стихии “почва”. После этого, хотя частота энергетической волны продолжает возрастать, в развитии системы, описываемой циклом триграмм или стихий, наступает спад. С этого момента данное описание можно перевести с регистрации изменения частотных характеристик на регистрацию характеризующего данный процесс изменения длины волны, что является очередным переключением с ян на инь, и если в первом полупериоде будет фиксироваться рост частоты, то во втором — убывание длины волны, причем математические выражения этого роста и убывания будут симметричны.

С другой стороны, симметричность относительно данного пункта прослеживается и в наборе величин, выражающих только один из параметров октавной шкалы, будь то частота колебаний, их период или длина волны. Геометрическим средним чисел 1 и 2, задающих октавное отношение, является Ö 2 (b = Ö 2 в формуле a/b = b/c, при a = 1 и c = 2), что, как показывалось выше, близко значению реконструированного хуан чжуна. Таким образом, система люй рассекается на две части, элементы которых могут быть выражены дробями с симметричными числителями и знаменателями.

Дата добавления: 2015-07-12