
Читайте также:
|
Современные исследователи классифицируют представления о времени как принадлежащие не только к субстанциальной или реляционной, но и к статической или динамической концепциям времени. Как указывает Ю.Б. Молчанов, в статической концепции прошлые, настоящие и будущие события мыслятся одинаково реальными. Различие между ними не объективно, а обусловлено “свойствами нашего сознания, которое, двигаясь вдоль своей “мировой линии” или жизненного пути, сталкивается с теми или иными событиями, переживает эти встречи как возникновение, исчезновение предметов и явлений”. В динамической концепции считается, что реально существуют только события настоящего времени. Что касается прошлых и будущих событий, то первые “уже реально не существуют, в настоящем остались лишь следы их существования, свидетельствующие об их прошлом бытии, а также воспоминания в человеческой памяти”, а вторые “не существуют вообще, есть только их предпосылки, зафиксированные в материальных связях и взаимодействиях настоящего и выражающие лишь возможность бытия будущих событий” (Молчанов 1980: 7).
Некоторые философы полают, что развитие статической и динамической концепций может привести к их синтезу (см., например: Подольный 1989: 21). Для этого в них должны быть урегулированы или сняты антагонистические черты. Эта проблема определенным образом решается в арифмосемиотике посредством подразделения потока времени на несколько слоев. В такой модели слои, выражающие постоянство, можно связать со статическим аспектом времени, а проявляющие соответственно изменчивость и сменяемость — с динамическим.
Сразу следует уточнить, что, поскольку арифмосемиотическая модель времени является реляционной, о статичности можно говорить только применительно к диапазону дления- цзю того или иного события, масштабы которого, правда, в силу регулятивности арифмосемиотических символов, могут варьироваться в широких пределах, вплоть до масштаба вселенной. Кроме того, время в арифмосемиотике, как указывалось выше, определяется только в совокупности всех своих слоев, но для упрощения рассуждений придется рассматривать их по отдельности.
Как известно, время связывается с изменениями. Нет изменений — нет и течения времени. Но событие как некая определенная единичность за весь период своего существования не изменяется. Изменяются только его отдельные черты. Не нарушают единства события и проходящие внутри него смены. Значит, оно в целом пребывает только в настоящем для себя времени. Этот аспект слоистого времени можно обозначить как “статическое настоящее”. В триграммной модели с порядком “взаимопорождения” ему будет соответствовать позиция Великого предела. Изменения и смены в событии можно рассматривать в качестве череды квантов, внутри которых наблюдается относительное постоянство. При этом, например, квант смены также существует только в своем настоящем времени. Однако это время имеет подвижное положение по отношению ко всей системе времени длящегося события. Поэтому его можно определить как “динамическое настоящее” (рис. 2.4.13, ср. рис. 2.4.12).
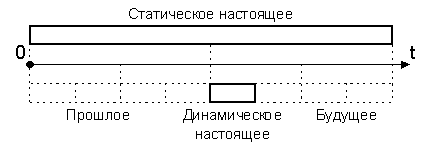
Рис. 2.4.13
Дление- цзю не может само по себе рассматриваться в качестве внутренней шкалы времени события по причине того, что оно постоянно и в нем нет собственных временных градаций. Можно говорить только об условных градациях, которые образуются при изменениях отношения верхней позиции к нижней, где находится квант смены. В построенной на условных градациях шкале времени конкретное положение кванта смены будет фиксировать момент настоящего, разграничивающий прошлое и будущее.
Во все эти времена постоянное в событии реально существует. По отношению к кванту смены оно как бы “выдвинуто” в прошлое и в будущее и зафиксировано в них, в чем и проявляется статический аспект модели слоистого времени. В отсутствии шкалы времени на основе дления- цзю для кванта смены нет ни прошлого, ни будущего, а есть только одно настоящее, что отражает динамический аспект данной модели.
Кванту смены присуще такое настоящее, которое имплицитно содержит в себе формы особого бытия прошлого и будущего — оттиски ушедшего состояния и ростки приходящего. Вместе они образуют механизм, благодаря которому настоящее постоянно возобновляется, меняя при этом свои конкретные черты.
В “Си цы чжуани” движение во времени объясняется с помощью образа “гусеницы-землемера” (чихо), свертывающейся и выпрямляющейся:
Уход-прошлое (ван) — это свертывание (цюй). Приход-будущее (лай) — это выпрямление (шэнь). Свертывание и выпрямление взаимовозбуждаются, и полезность образуется. Гусеница-землемер свертывается, чтобы после выпрямиться (Си цы, II, 3).
Приведенная в данном пассаже модель времени может относиться к динамическим. В ней объект не входит в уже существующее будущее, а “выкладывает” перед собой новое настоящее. То же самое можно воспроизвести в модели гусеничного привода, которая содержит в себе циклическую составляющую и тем самым сближается с моделью слоистого времени, построенной на цикле триграмм. В такой модели квант динамического настоящего можно рассмотреть в виде цикла, одна часть которого репрезентируется в настоящем, а другая — нет, но зато она собирает в себе прошлое и является источником будущего, которое “выкатывается” дискретными порциями на мнимую ось времени, делая ее реальной в пределах возобновленного кванта настоящего. Для полноты картины следует учесть, что цикличность в арифмосемиотике не является жесткой по причине подверженности влияниям разных внешних случайных изменений (рис. 2.4.14).
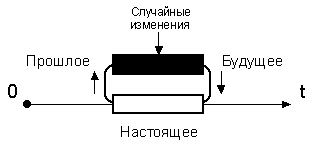
Рис. 2.4.14
В целом статико-динамическая модель времени демонстрирует возможность познать прошлое и будущее из настоящего. В первом приближении для этого всего лишь необходимо определить постоянную составляющую в событии. Правда, подобное познание прошлого и будущего — без знания конкретных сменяющихся аспектов события — будет представлять собой лишь его голый слепок. Но и такое проникновение за пределы настоящего кое-что значит. Для примера можно познакомиться с рассуждениями на тему познания будущего весьма далекого от арифмосемиотики, но наделенного житейской мудростью древнекитайского философа Мо-цзы (479—400):
Ученик Пэн Цин сказал: “Прошлое можно познать, но будущее нельзя узнать”. Учитель Мо-цзы ответил: “Предположим, что твои близкие живут за сто ли отсюда и сейчас испытывают большую беду. Исход дела решает один день. Если ты прибудешь в тот день, то они будут жить, нет — они погибнут. Перед нами находится крепкая повозка с хорошими лошадьми и другая, четырехколесная арба с разбитыми колесами, запряженная клячей. Тебе предоставляется сделать выбор, на чем ехать. На чем же ты поедешь?” Ответил: “Поеду на крепкой коляске с хорошей лошадью, так смогу быстрей доехать”. Учитель Мо-цзы тогда сказал: “Как же можно говорить, что нельзя узнать будущее?” (Мо-цзы 1994: 200).
Увы, и крепкая коляска может сломаться, и хорошая лошадь — подвести. По сути дела, такое познание будущего является лишь предположительным, основанным на знании общих свойств вещей. Более содержательный прогноз можно сделать в отношении событий, развивающихся по принципам порядков триграмм. Определив конкретный порядок и триграмму, соответствующую настоящему состоянию исследуемого события, можно без труда рассчитать, в какую фазу оно войдет через тот или иной промежуток времени. Этот расчет, разумеется, будет также приблизительным, поскольку не учитывает действие случайных изменений. Для последнего в арифмосемиотике предназначаются мантические методы “Книги перемен”.
2.5. “Магический квадрат” Ло шу
Ло шу и Хэ ту
Согласно древнекитайской легенде, Фуси увидел Ло шу (“Писание [из реки] Ло”) на панцире огромной черепахи, появившейся из реки Ло, а Хэ ту (“Чертеж [из Желтой] реки”) — на боку “дракона-лошади” (лун ма), появившегося из реки Хуанхэ. Первые литературные упоминания о Ло шу и Хэ ту относятся к эпохе “Борющихся царств”. Изображения этих схем, относящиеся к данному времени, до нас не дошли. Конкретных описаний также не имеется. Например, в “Лунь юе” (IX, 8) Конфуций только сетует, что в его время уже и “Феникс не прилетает, и чертеж (ту) не выходит из реки (хэ)”. В “Си цы чжуани” (I, 11) данным схемам посвящены следующие слова: “Из Хэ вышел чертеж, из Ло вышли письмена. Совершенномудрые берут их за образец (цзэ)”. В “Чжуан-цзы” (IV—III вв. до н.э.) Ло шу рассматривается как некая девятеричная схема, благодаря которой “осуществляются жизненные свойства вещи” (Чжуан-цзы 2002: 155). Во времена “Пять династий” (Удай) и в эпоху Сун в Китае появилось несколько схем, которые отождествлялись с древними Ло шу и Хэ ту. Этими схемами занимались Чэнь Туань, Шао Юн, Лю Му, Чжу Чжэнь и другие. Ло шу и Хэ ту в том виде, как они известны в настоящее время, были опубликованы в трактате сунского ученого Чжу Си (1130—1200) “Чжоу и бэнь и” (“Основной смысл “Чжоу и””). Их можно интерпретировать соответственно как “магический крест” и “магический квадрат” (подробнее см.: Henderson 1984: 82—87; КФЭС 1994: 399—401).
“Магический крест” Хэ ту не представляет собой ничего интересного с точки зрения рассматриваемых в настоящей книге идей, и поэтому здесь можно ограничиться только его описанием. Это схема, в которую входят десять чисел, обозначаемых светлыми (нечетные) и темными (четные) кружками (рис. 2.5.1). Располагаются они таким образом, что в центре и по четырем направлениям пространства разность двух чисел равна пяти.
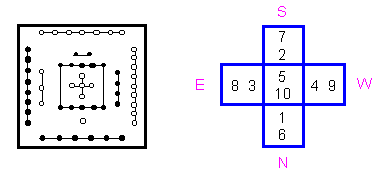
Рис. 2.5.1
Ло шу — это более содержательная схема числового баланса. Она связывает числа 1—9 по принципу “магического квадрата”, представляющего собой матрицу с тремя столбцами и тремя строками (рис. 2.5.2). Сумма чисел в каждом столбце, каждой строке и по диагоналям такой матрицы равна 15-ти.
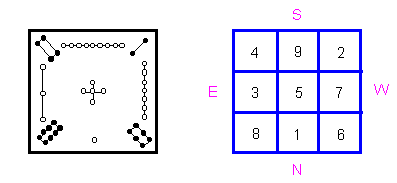
Рис. 2.5.2
К этому можно добавить, что результат деления числа 15 на количество строк или столбцов (3) равен 5-ти. Число 5 стоит в центре схемы, являя собой принцип равновесной середины. Остальные числа организуются вокруг него. Через центральную клетку проходят столбец, строка и две диагонали, в которых крайние числа больше или меньше центрального числа 5 на одинаковые значения. Большие числа можно рассматривать как янские, меньшие — как иньские, а число 5 — как нейтральное.
9 - 5 = 5 - 1 = 4;
8 - 5 = 5 - 2 = 3;
7 - 5 = 5 - 3 = 2;
6 - 5 = 5 - 4 = 1.
Преобразования Ло шу
Данная закономерность примет достаточно изящную форму, если воспользоваться методом Д.Р. Ионеску. Этот исследователь нашел, что между диаграммами Ло шу и Тай цзи существует некоторое специфическое отношение. Если из каждого числа Ло шу вычесть число 5, то получившиеся отрицательные и положительные числа образуют зоны, которые можно сравнить с графикой Тай цзи (рис. 2.5.3; см.: Ionescu 1972: 174—175).
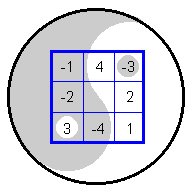
Рис. 2.5.3
Надо отметить, что отрицательные числа впервые упоминаются в книге “Искусство счета в девяти разделах” (“Цзю чжан суань шу”), написанной в эпоху Западной Хань. О более раннем их использовании в Китае ничего не известно. К тому же диаграмма Тай цзи оказывается в ходу у китайцев достаточно поздно, а именно в сунское время. Поэтому говорить о подобной структуре схемы Ло шу можно пока только в плане выявления ее чисто математических закономерностей.
С другой стороны, можно с полной определенностью утверждать, что, по крайней мере, с сунского периода китайцы производили различные преобразования Ло шу, причем некоторые из них можно интерпретировать на основе операций не вычитания, а прибавления чисел.
Так, в 1986 г. А.И. Кобзев обнаружил во входящем в “Дао цзан” (№ 1166 по К.М. Шипперу) сочинении “Фа хай и чжу” (“Жемчуг, оставленный морем законов- дхарм ”) преобразованный “полумагический квадрат” 3´ 3 (рис. 2.5.4), не описанный ранее в западной синологии (Кобзев 1986: 33, 43, сх. 6; 1993: 113, 374, сх. 6а) и представляющий собой числовую матрицу, в которой суммы чисел в правом столбце и нижней строке равны 9-ти, а по всем остальным направлениям — 18-ти (“полумагический квадрат” отличается от “магического” тем, что правило константной суммы действует не по всем направлениям).
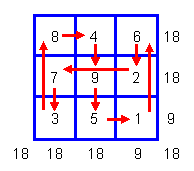
Рис. 2.5.4
Примечательно, что несколько ранее этот квадрат был реконструирован С.В. Зининым в рукописи “Человек и мир в китайской медицине” на основе анализа медицинских трактатов врачей Ван Вэйи и Ляо Шэнкуна, живших соответственно в сунскую и цинскую эпохи. Как отметил А.И. Кобзев, вычисление данного квадрата прежде его реального обнаружения является еще одним подтверждением того, что “в китайской традиции философские и научные тексты часто отличаются невыявленностью и даже намеренной зашифрованностью общетеоретических и общеметодологических оснований, выявление которых требует проведения специальных реконструктивных процедур” (Кобзев 1993: 113).
По А.И. Кобзеву, данный квадрат образуется из Ло шу посредством перемещения чисел по отмеченной на рис. 2.5.4 траектории. К этому можно добавить, что имеется иной способ преобразования, принципы которого можно использовать для получения подобных числовых квадратов, определенным образом связанных с некоторыми другими схемами китайской арифмосемиотики. Этот способ заключается, во-первых, в прибавлении ко всем числам Ло шу числа, равного 1 + 3n, где n = 0; 1; 2..., а во-вторых, в суммировании разрядов в получившихся числах. Для иллюстрации сказанного достаточно рассмотреть три первые числовые матрицы, полученные при прибавлении к Ло шу чисел 1, 4 и 7, поскольку они задают ритм повторения схожих числовых комбинаций (рис. 2.5.5).
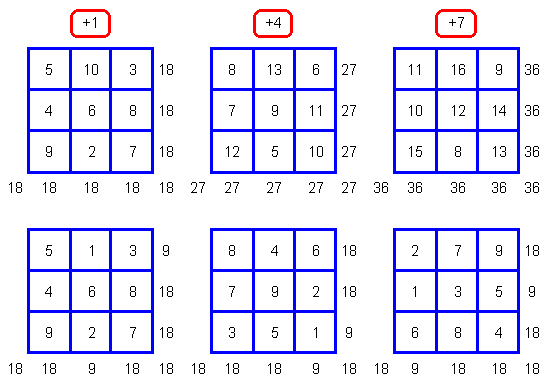
Рис. 2.5.5
Само собой разумеется, что в случае прибавления одного и того же числа к числам “магического квадрата” его свойства давать одинаковые суммы по всем направлениям будут сохранены, только эти суммы будут иными. Причем для прибавления можно использовать любое число. В ходе построения данных числовых матриц было использовано такое ограничение, согласно которому по одной из их диагоналей в конечном преобразовании размещаются в разном порядке числа, кратные 3-м — 3, 6 и 9. Таким образом, вместо числа 15 в первом случае получится 15 + 3 ´ 1 = 18, во втором — 15 + 3 ´ 4 = 27, в третьем — 15 + 3 ´ 7 = 36. При сложении разрядов во всех трех случаях суммы будут сокращены до 18-ти и до 9-ти. Причем последняя сумма получается каждый раз в одном столбце и в одной строке, на пересечении которых находится число 1, которое было образовано при сложении разрядов в числе 10. Если это сложение не делать, то в окончательно преобразованных квадратах суммы в соответствующих столбцах и строках также будут равны 18-ти.
Квадрат, представленный А.И. Кобзевым, будет соответствовать второму случаю — к Ло шу прибавляется число 4. Третий случай, возможно, еще ждет своего обнаружения в “Дао цзане” или каком-либо другом китайском тексте. Что касается первого случая, то выведение подобного квадрата совершенно иным способом, а именно за счет преобразования Хэ ту, было произведено М. Гранэ (Granet 1934: 198—200). В своей реконструкции последний опирался на оппозицию “земное-небесное”, которая воплощается в китайской традиции в числах 5 и 6, являющихся центральными для Хэ ту и Ло шу и получившейся числовой матрицы. При таком преобразовании расположенные в верхней и боковых частях Хэ ту числа 7 и 2, 3 и 8, 9 и 4 следует развернуть по схеме свастики, затем, поместив в центр число 6, а в нижнюю часть — числа 5 и 10, развернуть также последние (рис. 2.5.6). Образовавшийся квадрат будет отличаться по пространственной ориентации от того, который был получен выше за счет прибавления к Ло шу числа 1.
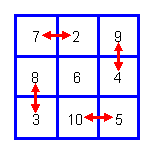
Рис. 2.5.6
Можно указать на еще один способ преобразования Хэ ту в Ло шу. В первой схеме надо поменять местами пары 2—7 и 4—9 и при этом переставить входящие в них числа. Затем также произвести разворот схемы по типу свастики. При этом получится обычный квадрат Ло шу, находящийся в традиционной пространственной ориентации (рис. 2.5.7).
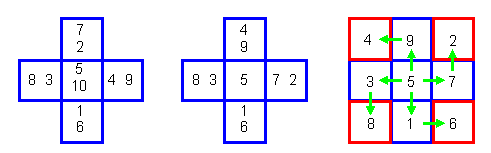
Рис. 2.5.7
Что касается пространственной ориентации Ло шу, то следует усомниться в том, что она была неизменной в китайской традиции. Вполне возможно, эта схема по своему расположению была вариативной, что требовалось для описаний тех или иных арифмосемиотических закономерностей. Кроме того, хотя и не известно, каким образом был составлен исходный Ло шу, но один из способов образования “магического квадрата” 3´ 3 предполагает операцию его разворота на один шаг.
Этот способ заключается в преобразовании простой числовой матрицы, в которой числа с 1 по 9 расположены по порядку слева направо и сверху вниз. Для начала следует поменять местами числа, находящиеся в противоположных углах. Если после этого развернуть матрицу на один шаг по часовой стрелке, то получится Ло шу в традиционном китайском ракурсе (рис. 2.5.8).
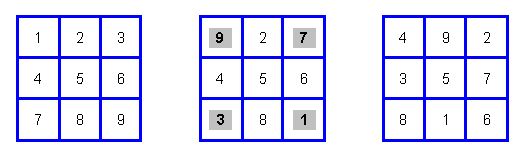
Рис. 2.5.8
Если же не разворачивать данную схему, то для того, чтобы в ней выполнялись “магические” правила, необходимо преобразовать ее в квадрат, вершинами которого окажутся числа, находившиеся ранее посередине сторон (рис. 2.5.9).
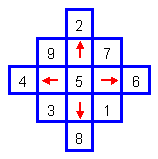
Рис. 2.5.9
Такую же ориентацию можно придать и тем трем “полумагическим квадратам”, которые были получены за счет сложения с числами Ло шу чисел 1, 4 и 7 (рис. 2.5.10). На это подталкивают хотя бы законы симметрии. Как уже говорилось, во всех этих матрицах по одной из диагоналей располагаются в разном порядке числа 3, 6 и 9. При развороте матриц на один шаг против часовой стрелки эти числа выстроятся по вертикали, выполняя функцию как бы некоей внутренне подвижной организационной оси, относительно которой происходят преобразования остальных чисел по треугольным траекториям.
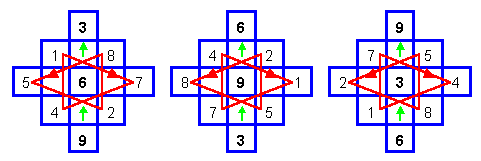
Рис. 2.5.10
Представленные в таком виде “полумагические квадраты” могут рассматриваться в качестве инструментов по преобразованию порядка “взаимопорождения” “младших” триграмм в “современный”. Если на базис-схему с порядком “взаимопорождения”, ориентированным в соответствии с реконструированными традиционными китайскими представлениями, наложить эти квадраты, то между их числами и триграммами установятся достаточно определенные связи (рис. 2.5.11). Говоря сразу о трех квадратах (+1, +4 и +7), числа которых приведены на схеме в соответствующих ячейках в последовательности слева направо, можно констатировать, что числа 1, 4 и 7 будут находиться вблизи триграммы 101, числа 5, 8 и 2 — 110, числа 4, 7 и 1 — 001, числа 2, 5 и 8 — 010, числа 7, 1 и 4 — 011, числа 8, 2 и 5 — 100.
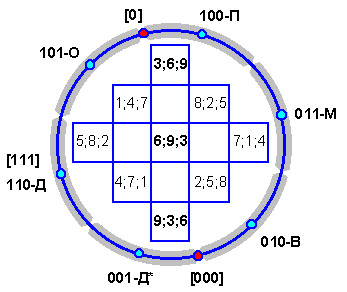
Рис. 2.5.11
Для полноты картины две из трех групп чисел, находящихся в вертикальной диагонали “полумагических” квадратов, следует связать с двумя “старшими” триграммами. Однако структура порядка “взаимопорождения” допускает вставку Кунь (000) только рядом с коррелирующей с ней триграммой Чжэнь (001). Это означает, что ее можно связать с нижней группой чисел (9; 3; 6). Триграмму Цянь (111) можно поместить только в соседстве с коррелирующей с ней Сюнь (110). Верхняя группа чисел никак не связывается с Цянь в таком положении, и поэтому данную триграмму логичнее будет сопоставить со средней группой (6; 9; 3). Таким образом, верхняя группа чисел (3; 6; 9) остается не связанной со “старшими” триграммами и будет обозначать точку баланса [0] всей схемы, если последнюю рассматривать на уровне символики 12-ти циклических знаков (см. рис. 2.2.3). Последние делятся пополам (1—6, 7—12) вертикальной диагональю “магических” квадратов, причем начала половин связываются с кульминационными периодами годичного и суточного циклов — полуночное и полуденное время суток, дни зимнего и летнего солнцестояния, а в пространственной символике эти начала соответствуют югу и северу.
Отталкиваясь от указанной корреляции триграмм и чисел, последние можно перенести на базис-схему с обратным “современным” порядком триграмм, имеющим традиционную ориентацию во времени и пространстве (рис. 2.5.12). При этом числа каждого из “полумагических квадратов” выстроятся в порядке перечисления с 1 по 9. Числа 3, 6 и 9, не имеющие корреляций с “младшими” триграммами, надо просто поместить в подходящее для них промежуточное место. На приведенной схеме получившиеся таким образом числовые ряды трех рассматриваемых квадратов (+1, +4 и +7) изображены в последовательности от внешнего круга ко внутреннему.
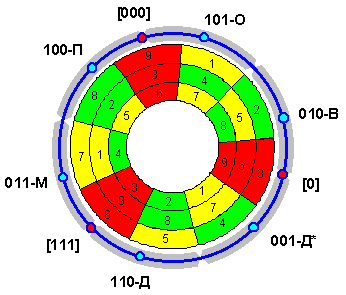
Рис. 2.5.12
Можно было бы поступить и иначе, а именно на круговую схему с числами с 1 по 9 поместить триграммы на основе их корреляций в схеме с “полумагическими квадратами” и порядком “взаимопорождения”. При этом по направлению перечня чисел получится обратный “современный” порядок “младших” триграмм, в который в определенных позициях вставлены “старшие” триграммы. При трехшаговых сдвигах числовых рядов, задаваемых правилом построения рассматриваемых квадратов, ракурс “современного” порядка будет оставаться неизменным. Эти сдвиги позволяют объединить числа 3, 6 и 9 в одних и тех же позициях, две из которых окажутся коррелирующими со “старшими” триграммами 111 и 000. Что касается самой круговой схемы с расположенными на ней девятью числами, то она является графическим выражением принципа сложения разрядов двузначных чисел, на основе которого были получены рассматриваемые “полумагические квадраты”. При продолжении счета после числа 9 двузначные числа становятся на позиции тех чисел, в которые они преобразуются при сложении разрядов. Иначе говоря, при этом производится их перевод в девятеричное счисление, при котором второй разряд не учитывается.
Подобные отношения между числами присущи гюрджиевской эннеаграмме, о которой говорилось выше (см. гл. 2.2, рис. 2.2.5). В ходе реконструкции, проводившейся в настоящей книге и других книгах автора (Еремеев 1993, 1996), были найдены многочисленные аналогии между структурой взаимоотношений триграмм и гексанемой, являющейся одним из компонентов эннеаграммы, связывающим в определенной последовательности шесть чисел (1, 4, 2, 8, 5, 7). Три остальных числа эннеаграммы — 3, 6 и 9 — объединены по треугольной связи, которую и демонстрирует получившаяся схема с числами и с обратным “современным” порядком триграмм. В эннеаграмме числа 3, 6 и 9 должны описывать “три толчка”, которые приводят в действие циркуляции, символизируемые остальными числами. У Г.И. Гюрджиева говорилось, главным образом, о символике циркуляций “энергий” между музыкальными нотами и между органами человеческого тела (см.: Успенский 1999: 505—506). “Младшие” триграммы также символизируют музыкальный звукоряд и органы, причем по очень схожим принципам. Двух “старших” триграмм оказывается маловато для сопоставления с гюрджиевскими “тремя толчками”, и ничего, что их могло бы дополнить, при исследованиях китайской арифмосемиотики не было найдено. Скорее можно предположить, что третьим компонентом является не некая сила, так или иначе влияющая на развитие описываемых триграммами циркуляций, а точка равновесия этих циркуляций, некий “нуль-пункт”, вокруг которого организуется та или иная схема триграмм.
Рассматриваемые здесь преобразования подтверждают данное предположение. Точка баланса годового или суточного ритмов в схеме “взаимопорождения” (см. рис. 2.5.11), являющаяся одним из выражений “нуль-пункта”, в схеме с обратным “современным” порядком займет место одной из вершин эннеаграммы (см. рис. 2.5.12). Как будет показано ниже, это местоположение “нуль-пункта” в производной схеме будет символизировать точку некоего психокосмологического баланса (см. рис. 2.9.8). Триграммы Цянь и Кунь, связанные с двумя другими вершинами эннеаграммного треугольника, примут при преобразовании традиционную корреляцию, присущую им в “современном” порядке, а именно: 111 — 011, 000 — 100.
По принципу построения базис-схемы, каждая из “старших” триграмм должна быть соотнесена с одной из соседствующих с ней “младших” триграмм, выбор которой обусловливается некими дополнительными соображениями. Например, если рассматривать получившуюся схему в медицинском аспекте, то Цянь будет обозначать “небесную пищу” — пневму- ци, поступающую в легкие, которые символизируются металлом и триграммой Дуй, а Кунь — “земную пищу” — обычную еду, поступающую в желудок, который вместе с селезенкой символизируется стихией “почва” и триграммой Гэнь. Таким образом, Цянь и Кунь, находящиеся в рассматриваемых позициях базис-схемы, действительно исполняют роль неких внешних “толчков”, приводящих в действие циркуляции внутренних энергий.
Дата добавления: 2015-07-12; просмотров: 102 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Случайность во времени | | | Ло шу и триграммы |